本文已参与好文召集令活动,点击查看:后端、大前端双赛道投稿,2万元奖池等你挑战!
本文发布在专栏 深入浅出webgl 中, 点击查看目录
如没有看过上一章: 深入浅出WEBGL - 01 - 点、向量、矩阵 建议查看
点的运动 - 向量
首先我们来说明一下点的运动这件事情。
在某坐标系下的点和向量都可以用一个竖着写的⎣⎢⎡xyz⎦⎥⎤ 去表示,当然二维点或向量是[xy] 去表示的。向量表示的是一个点的运动方向的,所以一个向量是具有长度和方向的。而点的坐标仅仅表示在某个坐标系下一个具体的位置。
怎么理解向量是点的运动呢? 这里我们回顾一下上篇文章中的一些运算:
- p~ + v
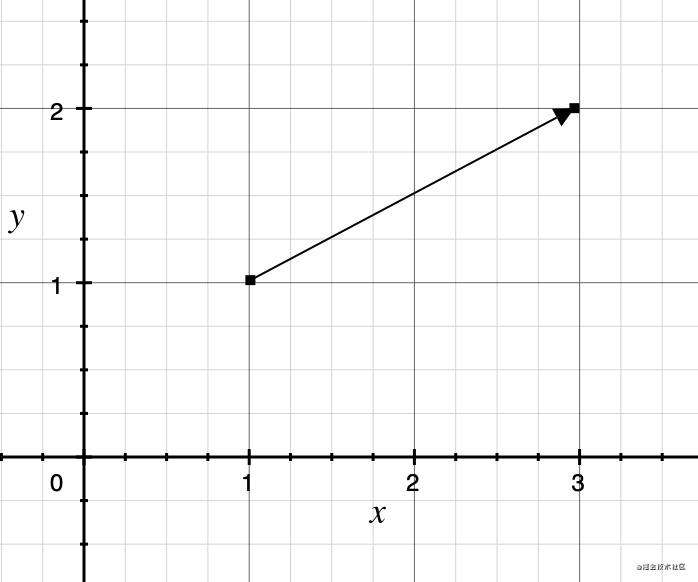
这代表这个点沿着这个向量的方向移动, 移动距离为向量的长度, 例如:
点[11] + 向量 [21] 得到的是点[32]
- p~1 - p~2
这个结果得到的是一个向量, 向量的方向是从点2指向点1
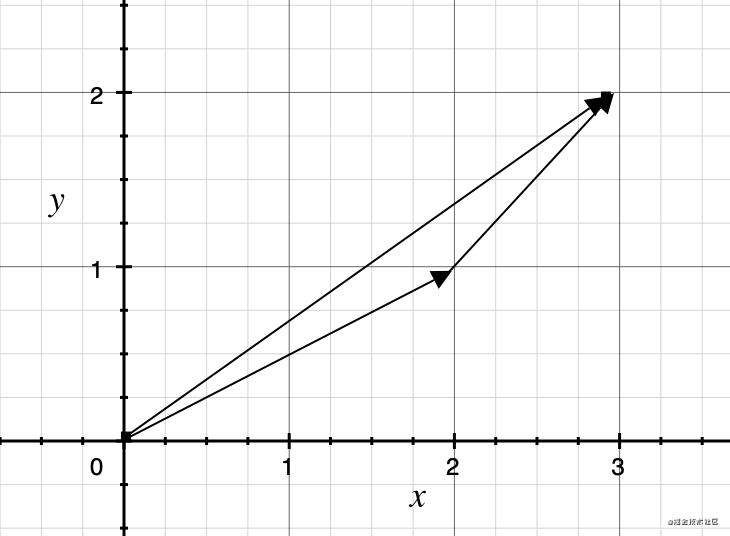
- v1 + v2
得到的结果是一个新的向量, 即两个代表点运动的向量相加得到了全新的一个代表点运动的向量, 新向量的运动结果跟之前两个向量代表的运动结果的叠加是相同的:
- 向量的点积
向量的点积公式:
v1⋅v2=∣∣v1∣∣∗∣∣v2∣∣∗cos(θ)常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!