几何函数
- 几何函数从统计学上近似的求得了微平面间相互遮蔽的比率,这种相互遮蔽会损耗光线的能量。
- 几何函数是一个值域为[0.0, 1.0]的乘数,其中白色或者说1.0表示没有微平面阴影,而黑色或者说0.0则表示微平面彻底被遮蔽。
- 几何项的影响可以间接地看作其对方向反射率(directional albedo)的影响
- 大多数材质的方向反射率(directional albedo)对于前70度是相对平坦的,并且切线入射处的反射率与表面粗糙度密切相关。
- 几何项的选择会对反射率产生影响,反过来又会对表面外观产生影响。
- 完全省略G项和1/cosθl cosθv项的模型,被称为“No G”模型,会导致在掠射角处过暗的响应。
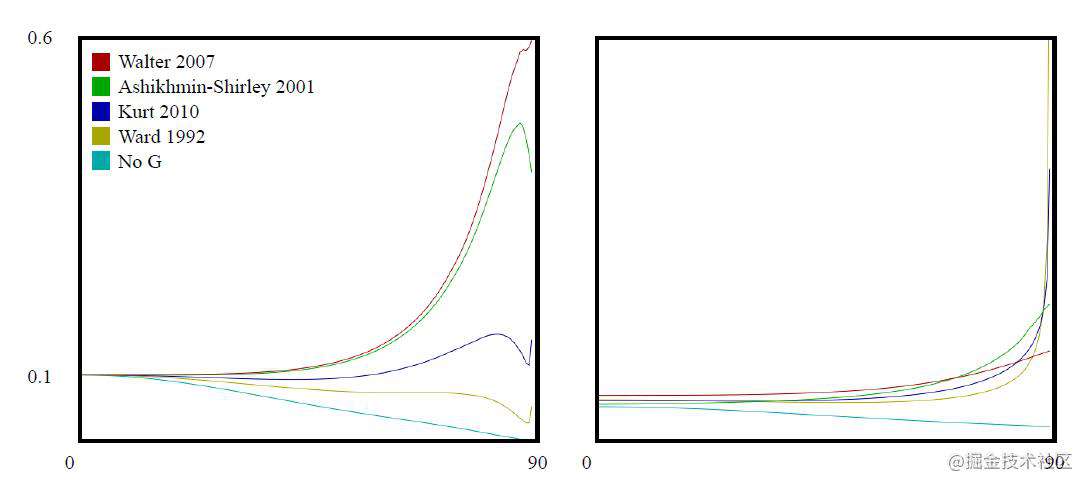 图 几种镜面反射几何模型的反射率图示。 所有图中都使用相同的D(GGX / TR)项和F项。 左图:光滑表面(α= 0.02); 右图:粗糙表面(α= 0.5)。 其中,“No G”模型已去除G和1/cosθl cosθv项的计算。
图 几种镜面反射几何模型的反射率图示。 所有图中都使用相同的D(GGX / TR)项和F项。 左图:光滑表面(α= 0.02); 右图:粗糙表面(α= 0.5)。 其中,“No G”模型已去除G和1/cosθl cosθv项的计算。
示意图

公式
公式1
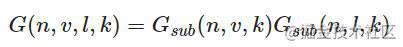
- G函数
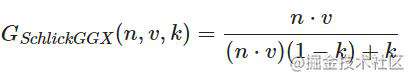
- K变量
- 直接光照
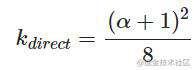
- IBL环境光
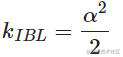
- 直接光照
- G函数
- 几何函数GLSL
公式2

- 将粗糙度参数进行重映射以减少光泽表面的极端增益,即将α 从[0, 1]重映射到[0.5, 1],α的值为(0.5 + roughness/2)^2。从而使几何项的粗糙度变化更加平滑
公式3
公式4
- 对于对清漆层进行处理的次级波瓣(secondary lobe),Disney没有使用Smith G推导,而是直接使用固定粗糙度为0.25的GGX的 G项,便可以得到合理且很好的视觉效果。
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!