前端也得懂点儿——排序算法

找最小数下标 minIndex

递归写法

let minIndex= (numbers) => numbers.indexOf(min(numbers)) 
let min = (numbers) => {
  if(numbers.length > 2){
    return min( [numbers[0], min( numbers.slice(1) ) ] )    // 递归
  }else{
    return numbers[0] < numbers[1] ? numbers[0] : numbers[1]
  }
}

缺点：代码繁琐（递归中使用了多层的括号、还引用了额外的帮助函数 min）

循环写法

let minIndex = (numbers) => {
  let index = 0 
  for(let i=1; i < numbers.length; i++){ 
    if( numbers[i] < numbers[index] ){  
      index = i 
    }
  }
  return index
}
minIndex([9,6,8,13,5,4])

• index 始终表示当前最小值下标，初始时假设当前最小值下标为 0
• 所以循环体中，应该从下标为 1 的元素开始抓取，依次和下标 0 的元素进行比较，将较小值下标赋给 index
• 全部遍历完，得到最小值下标

启发 ?

是的，这是已经被证明的事情

• 所有的递归，都可以改写成循环
• 如果觉得递归不好理解，都可以改写成循环，一般来说循环会更好理解，但循环写起来会更麻烦、代码量更大

循环的时候有很多细节

• 循环特别容易被细节干扰，这些细节很难想清楚，尤其是边界条件很难确定（动手列表格、找规律）
• 不用处理长度为 0 和 1 的数组（if length === 0 | 1 直接 return 即可）

如果 debug

• 学会看控制台、打 log（注意加标记）

​

​

选择排序 select sort

递归写法

• 数组长度大于 2，就找最小值放到前面，并对后面所有值再次 selectSort
• 数组长度等于 2，就直接比较大小 / 交换两个元素位置，然后返回数组（递归中止）
• 进入弹栈，执行多个 concat 拼接数组，最终得到顺序的数组

let selectSort = arr => {
  if (arr.length > 2) {
    let index = minIndex(arr)
    let min = arr[index]
    arr.splice(index, 1)
    return [min].concat(selectSort(arr))  // 递归
  } else {
    return arr[0] < arr[1] ? arr : arr.reverse()  // 中止
  }
}

let minIndex = arr => arr.indexOf(min(arr))

let min = arr => {
  if (arr.length > 2) {
    return min([arr[0], min(arr.slice(1))])   // 递归
  } else {
    return arr[0] < arr[1] ? arr[0] : arr[1]  // 中止
  }
}
selectSort([12, 5, 33, 4, 1])

循环写法

• 循环的每轮都假设：当前未排序数组的第一个元素就是最小值
  • 因为 i 始终表示未排序数组的最小值下标，所以 i 的初始值始终为 0
• 通过 minIndex 找到未排序数组中的最小值下标
• 如果最小值下标与假设不符，就通过 swap 交换位置

let selectSort = (numbers) => {
  for(let i = 0; i < numbers.length - 1; i++){   // ? 重点理解！！（边界：为什么-1）
    let index = minIndex(numbers.slice(i)) + i   // ? 重点理解！！（最小值下标：为什么+i）
    if(index !== i){ swap(numbers,index,i) }
  }
  return numbers
}

let swap = (array, i ,j) => {
  [array[i], array[j]] = [array[j],array[i]]
}

let minIndex = (numbers) => {
  let index = 0
  for(let i = 0; i < numbers.length; i++){
    if(numbers[i] < numbers[index]){
      index = i
    }
  }
  return index
}

selectSort([20,40,30,10])

​

为什么 - 1

暴力分析（逐步拆解）

let selectSort = (arr) => { 
  for(let i=0; i<???; i++){ 
    let index = minIndex(arr) 
    swap(arr, index, i)
  }
}

假设 arr 的长度为 n ，值为 4 ?

• 第一次循环 i = 0，当前遍历的元素下标为 0 ，需要进行比较的元素、其下标 index 的取值范围只能是 1\2\3

• 第二次循环 i = 1，当前遍历的元素下标为 1 ，需要进行比较的元素、其下标 index 的取值范围只能是 2\3

• 第三次循环 i = 2，当前遍历的元素下标为 2 ，需要进行比较的元素、其下标 index 的取值范围只能是 3

• 第四次循环 i = 3，当前遍历的元素下标为 3 ，需要进行比较的元素、其下标 index 无法取值

  • i 等于 3 时，在 minIndex(numbers.slice(3))中， numbers 只剩 numbers[3] 也就是 numbers[i] 本身，只剩一个元素，无法再和其他元素进行比较大小了，也就不需要 minIndex 操作了，所以 i = 3 是无意义的

  • 所以 i 不能等于 3，一定要 i = 3 和 一个空数组进行比较也可以，但多此一举

    

• 所以 i 的取值从 0 开始，最大就到 2 为止

• 结论：i 的取值范围是 i < 3 ，也就是 i < n-1

for(let i=0; i < numbers.length - 1; i++ ){...}

​

为什么 + i

当i=0，忽略0个，从[20,40,30,10]中找出最小值10/下标为【3】，实际在[20,40,30,10]对应下标仍为【3】
? [10, 40, 30, 20]

当i=1，忽略1个(下标为0的元素)，从[40,30,20]中找出最小值20/下标为【2】实际在[10,40,30,20]对应下标应为【3】
?[10, 20, 30, 40]

当i=2，忽略2个(下标为0/1的元素)，从[30,40]中找出最小值30/下标为【0】实际在[10,20,30,40]对应下标应为【2】
?不交换

得出规律

• i=0 时，minIndex => 3，index => 3 ? 相当于 minIndex + i = index
• i=1 时，minIndex => 2，index => 3 ? 相当于 minIndex + i = index
• i=2 时，minIndex => 0，index => 2 ? 相当于 minIndex + i = index

// 最终得出
let index = minIndex( numbers.slice(i) )  + i

双层 for 循环写法

let selectSort = arr => {
  for (let j = 0; j < arr.length - 1; j++) {  // j表示每轮遍历的元素的下标；i表示下一位元素的下标
    let minIndex = j  // 每轮都假设当前未排序数组的首位元素是最小值，其下标 j 是最小值下标
    for (let i = j + 1; i < arr.length; i++) { 
      if (arr[i] < arr[minIndex]) { //  当前元素与下一个元素，进行两两比较，找出最小值下标
        minIndex = i
      }
    }
    if (minIndex !== j) {  // 若最小值不是当前元素 j ，那就把最小元素与当前元素交换位置
      [arr[minIndex], arr[j]] = [arr[j], arr[minIndex]]
    } 
    // 每一轮都从未排序数组中找出最小值，并放到未排序数组的最前面(第一位)
    // 注：每一轮遍历的当前元素 j 所在位置，就是当前未排序数组的第一位
  }
  return arr
}

​

​

快速排序 quick sort

分析

let quickSort = arr => {
  if(arr.length <= 1) { return arr }   // 最基本的情况：发现指向的数组只剩下一个元素
  let pivotIndex = Math.floor(arr.length / 2)  // 获取基准的索引、找到靠中间的数字（取地板）
  let pivot = arr.splice(pivotIndex, 1)[0]  // 拿到基准数，将基准数从arr中删除，把arr分成左右两部分
  let left = []
  let right = []
  for(let i=0; i < arr.length; i++){   // 遍历被删掉基准数后的数组 （执行喊话操作）
    if(arr[i] < pivot){ 
      left.push(arr[i])  // 如果当前遍历元素小于基准数，就放到left数组中
    }else{
      right.push(arr[i]) // 由此得到了三部分：左边数组、基准数、右边数组
    } 
  }
  return quickSort(left).concat( [pivot], quickSort(right) )  // ? 代码的核心就是这句 ??
  // 不断对左边数组快排、右边数组快排、连接两边数组和基准数
  // 停止条件是 数组只剩下一个元素，直接返回数组，不用再比较大小
}

• splice 会修改原数组，返回值是被删除的元素组成的数组
• pivot /ˈpɪvət/ —— 基准、中心点、轴
• 取地板（舍去小数部分）：Math.floor(3.5) → 3

纯净代码

let quickSort = arr => {
  if(arr.length <= 1){ return arr }
  let pivotIndex = Math.floor(arr.length / 2)
  let pivot = arr.splice(pivotIndex,1)[0]
  let left = []
  let right = []
  for(let i=0; i<arr.length; i++){
    if(arr[i] < pivot){ left.push(arr[i]) }
    else{ right.push(arr[i]) }
  }
  return quickSort(left).concat([pivot], quickSort(right))
}

​

​

归并排序 merge sort

函数 mergeSort 思路

• 拿到一个乱序的数组，会把数组拆分成左右两部分。
• 然后对左右两边再次进行 mergeSort 递归拆分，拆分到所有元素独自成一个数组，达到中止条件。
• 开始回归，两两数组进行 merge 合并
  • 此时左右两边的数组只有两种情况：①两个长度为1的数组，②一个空数组 & 一个长度为1的数组

函数 merge 思路

• 接收两个数组作为参数（只接收排好序的数组，长度为1的数组也属于排好序的数组）
• **每次都比较两个数组的首项，并提取出较小的值，放在最前面 ** 因为两个数组都是顺序排列，所以首项一定代表其所在数组的最小值。 两个最小值对比得出的较小值，一定是所有元素中的最小值，所以摘出放在最前面
• 对数组中的剩余元素，继续重复上一步的 merge 操作（递归）

let mergeSort = arr => {
  if (arr.length === 1) {  // 长度为1的数组，无需排序，所以默认它是已经排好序的数组【这点非常关键】
    return arr
  }
  // arr.slice(begin,[end]) 截取数组下标从begin到end的部分，返回新数组（包括begin，不包括end）
  // slice不改变原数组。省略 end 参数，会一直提取到原数组末尾
  let left = arr.slice(0, Math.floor(arr.length / 2)) // left是从下标0截取到一半的位置（不包括end）
  let right = arr.slice(Math.floor(arr.length / 2)) // right是从一半的位置，截取到末尾（包括begin）
  return merge(mergeSort(left), mergeSort(right)) 
  // 左右再次进行拆分操作。拆到数组只有1个元素，认为所有数组已经排好序。（开始弹栈，执行 merge）
  // 对排好序的数组进行 merge 合并（这才是归并算法的核心?见下）
}

let merge = (a, b) => {  // 【前提条件：merge 接收的a、b两个数组，必须是已经排好序的两个数组】！！！
  if (a.length === 0) return b  // 一个空数组a和一个已经排好序的数组b，那就直接返回排好序的数组b
  if (b.length === 0) return a  // 同理
  return a[0] > b[0] ? [b[0]].concat(merge(a, b.slice(1))) : [a[0]].concat(merge(a.slice(1), b))
  // ?这里就是递归的难理解之处，需要拆解步骤⚠️⚠️，见下
}

slice：不改变原数组

• arr.slice(begin, end)：截取下标从 begin 到 end 的部分（包括 begin，不包括end），返回一个新数组
• arr.slice(begin)：截取下标从 begin 到数组最后一个元素，返回一个新数组

拆解 merge

   merge([1,5,10], [2,4,9])
=> a[0] > b[0] ? [b[0]].concat(merge(a, b.slice(1))) : [a[0]].concat(merge(a.slice(1), b))
---------------------------------------------拆解 ?-----------------------------------------
// 第一步：指向两个数组的第一位，比较大小
=> [1,5,10], [2,4,9]  
    ↑         ↑       
   1 > 2 否，执行 [a[0]].concat( merge( a.slice(1), b ) ) // 相当于把较小值摘出，再次merge剩余部分
=> [1, merge( [5,10], [2,4,9] )]
               ↑       ↑
   5 > 2 是，执行 [b[0]].concat( merge( a, b.slice(1) ) ) // 把较小值摘出，再次merge剩余部分
=> [1, 2, merge([5,10], [4,9]) ]
                 ↑       ↑
   5 > 4 是，执行 [b[0]].concat( merge( a, b.slice(1) ) ) // 把较小值摘出，再次merge剩余部分
=> [1, 2, 4, merge([5,10], [9]) ]
	                  ↑       ↑
   5 > 9 否，执行 [a[0]].concat( merge( a.slice(1), b ) ) // 把较小值摘出，再次merge剩余部分
=> [1, 2, 4, 5, merge([10], [9]) ]
		                   ↑     ↑
   10 > 9 是，执行 [b[0]].concat( merge( a, b.slice(1) ) ) // 把较小值摘出，再次merge剩余部分    
=> [1, 2, 4, 5, 9, merge([10], []) ]   
   											 ↑    ↑
   // 满足中止条件：一个空数组、一个已经排好序的数组 ，那就直接返回排好序的数组b
=> [1, 2, 4, 5, 9, 10]

简图

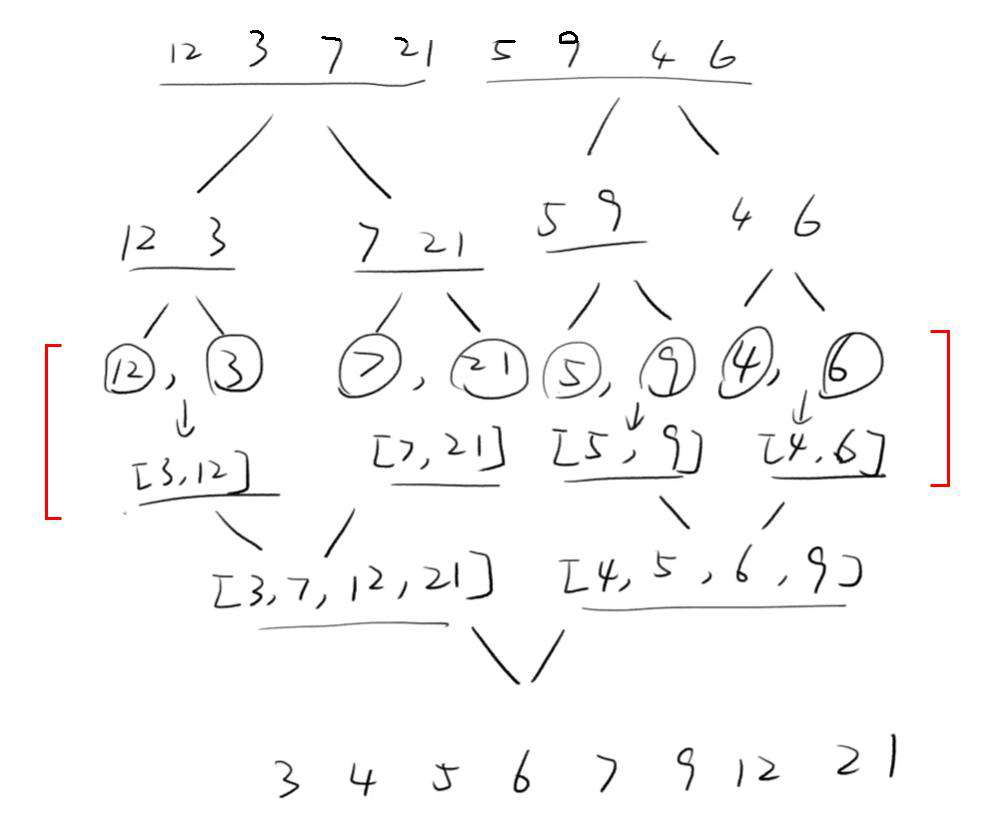
纯净代码

let mergeSort = arr => {
  if (arr.length === 1) {
    return arr
  }
  let left = arr.slice(0, Math.floor(arr.length / 2)) 
  let right = arr.slice(Math.floor(arr.length / 2))
  return merge(mergeSort(left), mergeSort(right))  
}
let merge = (a, b) => {
  if (a.length === 0) return b
  if (b.length === 0) return a
  return a[0] > b[0] ? [b[0]].concat(merge(a, b.slice(1))) : [a[0]].concat(merge(a.slice(1), b))
}

​

​

​

计数排序 counting sort

思路

• 用一个新的数据结构 —— 哈希表，来作记录
  • 哈希表：一种 key: value 的形式。
  • JS 的对象可以算是哈希表的一种形式，但不是纯粹的哈希表。
  • 因为 JS 对象具有隐藏属性、函数，而真正的哈希表里没有隐藏属性，只有数据。 所以 JS 对象不能算是一个完全的哈希表
• 发现数字 N 就记 N：1，如果再次发现 N 就加 1 …
• 最后把哈希表的 key 全部打出来，假设 N：m，那么 N 需要打印 m 次

分析

• 遍历数组，得到一个 hashTable（记录出现过的元素 key，以及出现次数 value）。
• 同时，在这次遍历数组的过程中，找到数组最大值 （开局假设第一个元素就是最大值max，依次比较，大于 max 的元素，就重新赋值给 max）
• 此时，已知 hashTable 和 max。
• 已知最大值 max，所以全部元素的取值都在 0 ~ max 这个范围之间
• 遍历 0 ~ max 这个范围之间的所有元素，如果与哈希表的 key 一致，就之间把这个元素 push 到数组中
  • 如果当前 key(元素) 的 value(出现次数) 不是 1，说明原数组中有 N 个该元素，那就需要把 N 个该元素都在此时 push 到数组中。所以 push 操作需要循环执行 N 次
  • 获取这个 value 次数，作为 for 循环执行次数 i 的依据，来控制 push 的执行轮次

let countSort = arr => {
  let hashTable = {}, max = 0, result = []
  for(let i = 0; i < arr.length; i++){  // 遍历原数组，得到一个 hashTable，以及最大值 max
    if(arr[i] in hashTable){
      hashTable[arr[i]] += 1 
    }else{
      hashTable[arr[i]] = 1
    }
    if(arr[i] > max){ max = arr[i] }
  }
  for(let j = 0; j <= max; j++){ // 遍历长度为max的数组，实现对原数组元素的排序
    if(j in hashTable){
      for(let i = 0; i < hashTable[j]; i++){  
        // 假设 j 出现了 3 次，就需循环 3 次(添加 j)的操作。
        // i 可以取几个值，循环就执行几次，所以 i 应该取 3 个值 （从0开始就取 i = 0，1，2）
        result.push(j)
      }  
    }
  }
  return result
}

计数排序的特点 ✅

• 使用了额外的 hashTable （数据结构）

  • 计数排序中使用的数据结构升级了
  • 算法也就直接升级了，非常快

• 只需要遍历原数组一次（再遍历一次 hashTable 即可）

  • 之前的排序算法，都会多次遍历数组
  • 如，选择排序：先找第一个最小值，遍历一遍数组。找第二个最小值，再把余下元素遍历 … 往复

• 为什么计数排序，可以这么厉害，就遍历一遍原数组呢？

  答：就是因为有 hashTable，这叫做「用空间换时间」

  • hashTable 就是存储在内存中的一块空间。
  • 用多余的空间就可以节省多余的时间。
  • 通常，空间、时间只能二选一：「用空间换时间」或「用时间换空间」

题外话：字母出现次数

let count = str => {
  let result = {}
  let newStr = str.replace(/[^a-zA-Z]/g, '')   // `HiImSam`
  console.log(newStr)
  for(let i=0; i<newStr.length; i++){
    if(newStr[i] in result){
      result[newStr[i]] += 1
    }else{
      result[newStr[i]] = 1
    }
  }
  return result
}
let str = `Hi, I'm Sam`
let newStr = str.match(/a-zA-Z/g)
count(str)
--------------------------------------------------
{
  H: 1
  I: 1
  S: 1
  a: 1
  i: 1
  m: 2
}

补充正则

提取数字....value.replace(/[^\d]/g, '')
提取中文....value.replace(/[^\u4E00-\u9FA5]/g, '')
提取英文....value.replace(/[^a-zA-Z]/g, '')

例

let str = `Hi, I'm Sam`
let newStr = str.match(/[a-zA-Z]/g)  //  ["H", "i", "I", "m", "S", "a", "m"]
// match 返回数组

let str = `Hi, I'm Sam`
let newStr = str.replace(/[^a-zA-Z]/g, '')  // `HiImSam` （把字符串中所有非字母字符，替换为空）
// replace 返回字符串 （替换思想）

​

​

​

还有哪些排序算法 ⁉️

冒泡排序 visualgo.net/zh/sorting 点击 BUB （visualgo只提供伪代码思路参考）

插入排序 visualgo.net/zh/sorting 点击 INS

希尔排序 sorting.at/ 自己选择 Shell Sort

基数排序 visualgo.net/zh/sorting 点击 RAD

冒泡排序 bubble sort

思路

• 两两对比，较大的往后接着对比。
• 每一轮找出一个最大值，冒泡到最后

let bubbleSort = arr => {
  for(let i = 0; i < arr.length - 1; i++){    // i 代表轮次（两两比较）
    for(let j = 0; j < arr.length - i; j++){  // j 代表当前轮选中元素的下标
      if(arr[j] > arr[j+1]){
        [arr[j], arr[j+1]] = [arr[j+1], arr[j]]  // 交换元素
      }
    }
  }
  return arr
}

​

插入排序 Insertion Sort

• 拿起一张牌，依次和前面的牌对比（所以起始值从下标为 1 的元素开始，才能保证前面有值可对比）

• 比前面的小，就插入到前面去

思路

1. **从第一个元素开始，该元素可以认为已经被排序 **
2. 取出下一个元素，**在已经排序的元素序列中从后向前扫描 **
3. 把取出的元素放到已排序的元素中间的合适位置
4. 重复步骤 2~3

就像排队一样，依次每次挑一个同学，把该同学“插入”到已经排好的部分队伍里。

代码

• 开局默认第一个元素（前面元素）是已经排好序的。
• 取出下一个待排序元素，与前面已排好序的元素进行比较
• 如果后面的元素小于前面已排好序的某个元素，就把后面元素插入到前面已排好序的元素的**相应位置 **

// 插入法JS版
function insertionSort(arr) {
  // 开局默认下标0的元素已排序，所以待排序数组的下标取值从1开始
  for(let i = 1; i < arr.length; i++) {
    // i 表示当前待排序数组元素的下标
    // j 表示当前已排序数组元素的下标（默认下标0的元素已排序,所以 j 初始值一定为0）
    // 已排序元素始终在待排序元素的前面，所以 j 的取值一定小于 i
    // 综上 j = [0,i)
    for(let j = 0; j < i; j++) { 
      // 当前取出的待排序元素arr[i]，依次和前面已排序元素进行比较
      if(arr[i] < arr[j]) {  
        arr.splice(j, 0, arr[i])  // 在 arr[j] 前面插入 arr[i]，然后把原本的 arr[i] 删除
        arr.splice(i+1, 1) // 因为上一步已经在前面插入一个元素，导致后面元素下标后移一位，原本需要被删除 i 位置上的元素，现在的下标变成了 i+1
        break  // 跳出内层循环，i++
      }
    }
  }
}
let arr = [10, 34, 21, 47, 3, 28]
insertionSort(arr)
console.log(arr)

补充：普通版 for 循环

function insertionSort(arr) {
  for(var i = 1; i < arr.length; i++) {
    var temp = arr[i]
    for(var j = i; j > 0 && arr[j-1] > temp; j--) {
      arr[j] = arr[j-1]
    }
    arr[j] = temp
  }
}
-----------------------------------------------------
function insertionSort(arr) {
  for (var i = 1; i < arr.length; i++) {
    var temp = arr[i];
    for (var j = i - 1; j >= 0; j--) {
      if (arr[j] > temp) {
        arr[j + 1] = arr[j];
      } else {
        break;
      }
    }
    arr[j + 1] = temp;
  }
  return arr;
}
-------------------------------------------------------
let arr = [10, 34, 21, 47, 3, 28]
insertionSort(arr)
console.log(arr)

补充：普通版 while 循环

function insertionSort(arr) {
  for (var i = 1; i < arr.length; i++) {
    var temp = arr[i];
    var j = i - 1;
    while (j >= 0 && arr[j] > temp) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = temp;
  }
  return arr;
}
let arr = [10, 34, 21, 47, 3, 28]
insertionSort(arr)
console.log(arr)

​

希尔排序 Shell Sort

• 极其少见
• 算法属于比较复杂的。现实生活中没有可参考的例子、数学中也没有例子
• 1959年，一个叫 Shell 的人发明的

​

基数排序 Radix Sort

特别适合用于**多位数排序 **

• 指未排序数组中的元素，有一位数得、也有两位数、三位数、四位数、五位数的 … （形式多样的数组）
• 死记硬背，顺序非常重要，记错了就完了（但是可以理解这个算法的精神 ? ）

• 先根据个位数排序，个位是 0 的从下往上叠在一起，个位是 1 的从下往上叠在一起 …
  • 然后按照个位 0-9 堆叠的从下往上的顺序（这个顺序非常重要）展开所有元素，成一个数组
• 对这个新数组，根据十位数进行排序，十位数 0-9 从下往上堆叠。
  • 然后再按0-9从下往上的顺序展开成数组
• …
• 所有位数都重复上述操作
• 最后展开的数组，就是排完序的数组

​

堆排序 Heap Sort

• 堆排序应该是排序的终点了，因为没有比堆排序更复杂的排序了
• 所有其他复杂的排序，基本都是在堆排序的基础上进行改进而已
• 搞定了堆排序，就搞定了「树」（数据结构），就搞定了排序最难的一部分