WebGL学习-数学篇

第一篇：WebGL基础

前言

这是WebGL学习的第二篇，今天主要说说WebGL中用到的一些数学的东西，里面并没有什么特别高深，特别难的点，都是高中大学学过的一些东西，却是图形学中非常重要的基础，所以本篇也是后续学习的基石。

向量

向量是“老朋友了”，首先就来看看他。

向量就是带方向的线段，因此向量包含两个意思，一个就是要有一个方向，另外就是有一个长度。根据这个概念又可以引申出标量的概念，所谓标量就是没有方向的线段。

在数学上向量是这么表示的：

使用一个字母，在上面加上一个箭头就表示一个向量。向量的长度则可以使用‘||’双竖线表示，一些教材上也会使用两个双竖线来表示向量的长度，这里为了便于理解，统一都使用一个双竖线表示。

向量中包含了一些特殊的向量，比如下面说到的单位向量。

单位向量

所谓单位向量就是长度为1的向量，通常只表示方向，后面说到向量归一化，实际就是将向量归一化为单位向量。

单位向量一般用一个^表示，读作hat，帽子的意思，例如单位向量a可以读作a hat。

在图形学中，用的比较多的就是向量的点乘和叉乘两个运算。其实向量也有加减法，一般我们都是说加法，减法就是负向量相加，所以是一样的运算。

下面就简单说下向量的运算。

向量加法

向量加法一般使用平行四边形法则来解决，当然也可以使用三角形法则来做。从上图中就能很容易看到最长的那个向量a就是向量v和向量u相加的结果，并且也满足加法的交换律，但是减法就不一样了，减法得到的结果是向量w，可能会有人疑惑，这个怎么组成平行四边形的呢？

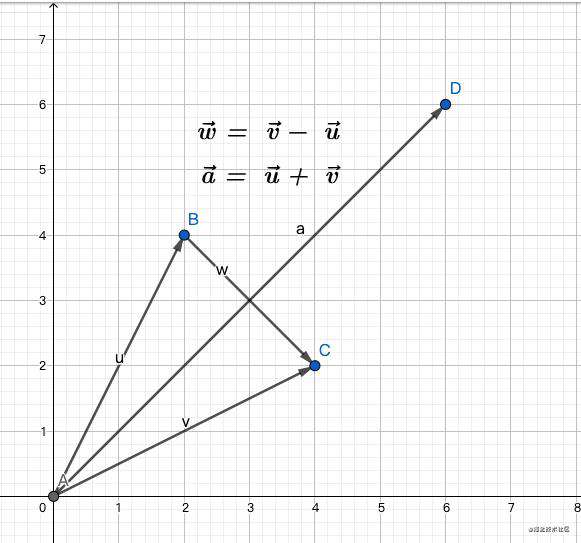
这下能看出来相减的结果实际是第四象限的向量b，因为向量w和向量b长度相等，方向相同，因此这两个向量是相等的，所以为了便于计算，我们把向量b作为向量v减去向量u的结果。

如果用三角形法则的话，来看上图的向量v就是向量u和向量w的首尾相连组成的三角形最终得到的向量v。

然后我们来验证下向量加减是这么去计算的，按照图上的坐标，很容易就能得到下面的结果：

向量a = (向量v的x坐标 + 向量u的x坐标, 向量v的y坐标 + 向量u的y坐标)

向量w = (向量v的x坐标 - 向量u的x坐标, 向量v的y坐标 - 向量u的y坐标)

需要注意的是减法没有交换律的，如果交换两个操作数，那么得到的结果也是不一样的。

向量的加减说完了，再来就是图形学中用的比较多的运算：点乘和叉乘。

向量的点乘

点乘运算一般都是这么表示：

向量b · 向量c

点乘的结果就叫做点积，点积是一个标量，为什么这么说呢，来看下点积是如何计算就明白了。

假如有两个向量，分别是向量a(x1, y1)，向量b(x2, y2)，那么他们的点积就是这么来计算的:

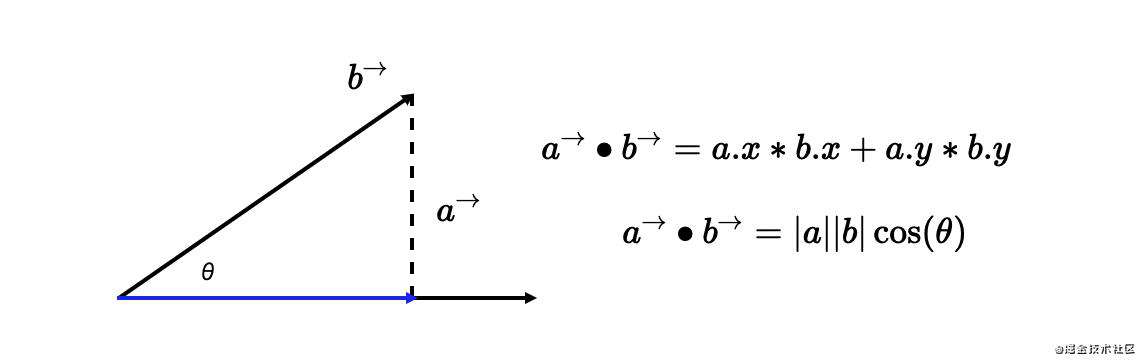
上图第一个式子很容易理解，就是两个向量的坐标相乘以后相加。而第二个式子也是在图形学中有非常重要的应用。其实根据上图也能容易看出向量b的长度乘以他们的夹角，实际就是这个直角三角形的底边。

我们再次带入值去验证一下，假设向量b的坐标为(2,2)，向量a的坐标为(5, 0)，他们之间的夹角为45度，那么分别应用两个公式就可知：

# 式一
向量a • 向量b = 2*5 + 2*0 = 10

# 式二
向量a • 向量b = 5 * bcos(45°) = 5 * 2√2 * (√2 / 2) = 10

所以向量的点乘的几何意义就是a 向量乘以 b 向量在 a 向量上的投影分量

有了上面的分析，那么就可以做出一些特殊情况的推导：

1. 如果向量夹角为0，也就是相互平行，那么余弦值就是1，其点积就是两个向量的长度相乘。

2. 如果向量夹角为90°，即相互垂直，余弦值为0，那么点积结果也就是0。

点乘还是比较简单的，而叉乘则是相对复杂一点的运算。那么再次复习一下叉乘的一些概念吧

向量的叉乘

向量的叉乘一般这么表示：

向量a ✖️ 向量b

向量叉乘的结果叫做叉积，这和点积是一样的。需要注意点积是一个标量，但是叉积是还是一个向量。

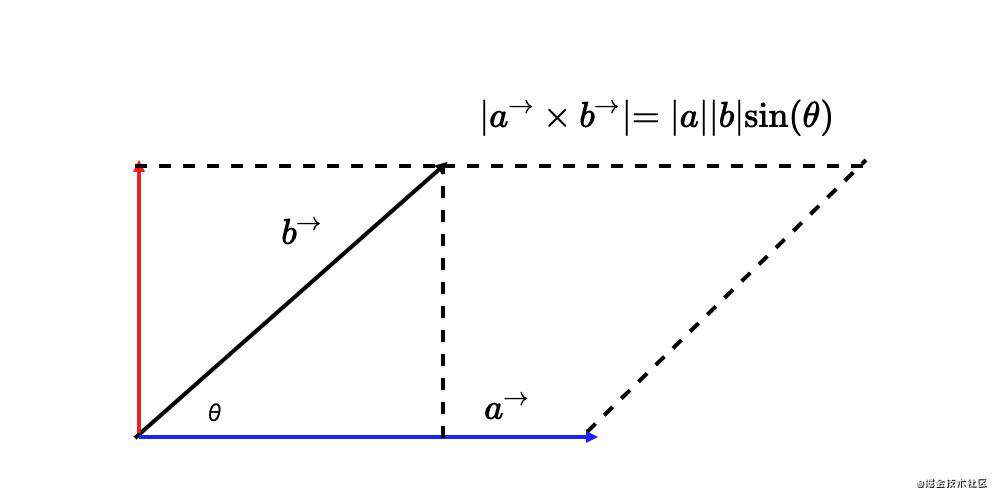
如上所示，在二维空间中，向量的叉乘运算就是两个向量围成的平行四边形的面积，或者说是向量a与(向量b在向量a的垂直方向，也就是红色箭头线段上的投影)的乘积，也就是红色和蓝色箭头围成的矩形面积。(这段话比较绕，需要好好体会)。

这是叉乘在二维空间中的几何意义，推广到三维的话，叉积就是垂直于两个向量围成的平面。这么说不太好理解，来看下图片就明白：

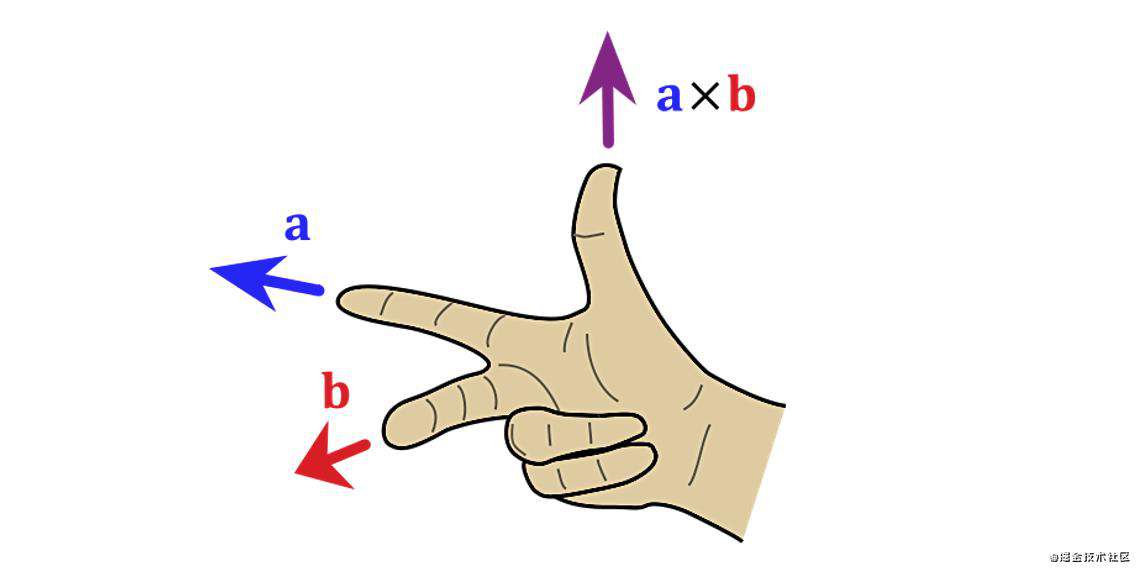
这也是上篇提到的右手定则。其实我们也可以使用更加简单的右手螺旋定则来确定叉积的方向。例如上图中的向量a叉乘向量b，我们伸出大拇指，将剩下四个手指并排伸开，按照从a到b的方向旋转，这样大拇指所指的方向就是两个向量叉积的方向了。

接下来就说说如何计算叉积。上图已经显示了叉积计算的公式就是两个向量的长度相乘，再乘上他们夹角的正弦值。

a × b = [y1 * z2 - y2 * z1, - (x1 * z2 - x2 * z1), x1 * y2 - x2 * y1]

这里我们使用了三维向量来表示，如果是在二维空间中，那所有的z的值都为0，于是两个向量的叉乘就是：

a × b = x1 * y2 - x2 * y1

知道了向量的叉乘，那么就来看看向量叉乘的一些应用。例如求某个点到某个向量的距离。

根据上面所说，向量的叉乘的结果就是两个向量的平行四边形的面积，那么利用叉乘，立刻就能知道这个平行四边形的面积，然后再除以底边的向量，得到的就是另外一个向量到底部向量的垂直距离，也就是我们需要求的结果。

说完了点乘和叉乘，他们在图形学中又如何应用呢？别急，这就到了开头所说的归一化。

向量的归一化

归一化就是将向量除以自己的长度，从而变成单位向量，如果向量都是单位向量的话，则上面得到的公式又可以简化：

# 点乘
a • b = |a||b|cos? = cos?

# 叉乘
a × b = |a||b|sin? = sin?

我们又能知道，如果两个向量都是单位向量，就能立刻得到这两个向量的正弦值和余弦值，根据这两个值就能得到两个向量的夹角。这点在后续的绘图中非常重要，也是向量运算的一个意义所在。

说完了向量，另一个要说的就是矩阵。可是已经有了向量来表示图形，为何还要有矩阵呢？原因就是向量表示的信息比较少，就只有长度和方向两个信息，如果我们要做一些复杂的变换，那么使用向量就会变得难以计算和理解，为此，矩阵也是我们需要学习的重要基础。

矩阵

再说矩阵之前，上面我们所说的向量一般我们都是这么表示

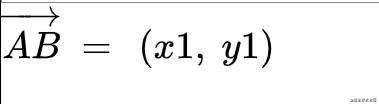
这叫做行主序，意思就是按行来读取。另外一种就是列主序，像这样

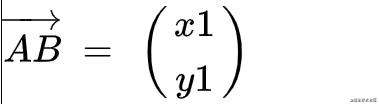
所以这么看，二维向量就是一个两行一列的矩阵。向量是有点乘和叉乘的运算，矩阵也是存在相乘运算。

矩阵相乘有两种，一种就是矩阵乘以一个标量，这个是和向量乘以一个标量是一样的，另外一个则是矩阵乘以一个矩阵，但是两个矩阵相乘是有一些限定条件的，例如，对于一个二行三列的矩阵，能与之相乘的矩阵需要是一个三行n列的矩阵，为什么会有这种限制呢，我们来计算一下就明白了。

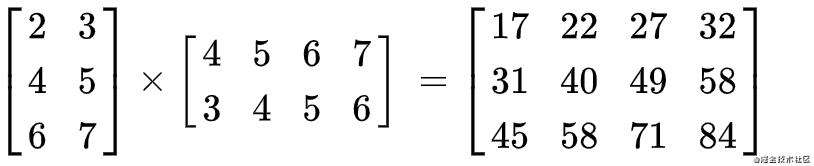
这里的结果是按照下面这么来计算的：

结果矩阵i行j列 = 矩阵a的i行1列*矩阵b的1行j列 + 矩阵b的i行2列*矩阵b的2行j列

这里学过线性代数的小伙伴应该都清楚，就不再赘述了。

因为向量也能看成是一个矩阵，所以矩阵也可以与向量相乘，结果也是按照上面的算法来计算的。需要注意矩阵乘法和向量的叉乘一样，没有交换律的，但是存在结合律和分配率，这点在图形学中会经常用到。

另外还有一种特殊的矩阵叫做单位矩阵

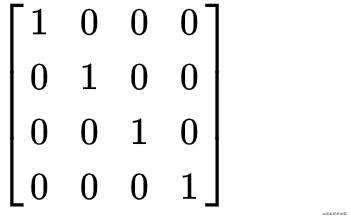
就是对角线都为1的矩阵，按照上面的计算规则可以发现，任何矩阵乘以单位矩阵还是等于它本身。那么单位矩阵又什么作用呢？这就又有了下面的一个概念。

逆矩阵，就是矩阵A乘上矩阵B等于矩阵B乘上矩阵A，并且他们相乘的结果就是单位矩阵。这里就简单复习了一些矩阵的相关概念，感兴趣的同学可以翻到底部，查看给出的参考资料来继续学习。接着就到了本篇重点复习的内容，变换。

对于一个向量来说，它可以在空间中进行各种变换，这些变换主要包括了以下三种：

1. 缩放
2. 旋转
3. 平移

需要了解的是缩放和旋转是一种线性变换，线性变换和平移变换合在一起统称为仿射变换，它也是图形学中各种变换的基础。那么仿射变换和矩阵又有什么联系呢？

我们来一一说说这三种仿射变换以及和矩阵的联系。

缩放矩阵

先看缩放，一般将一个向量进行缩放实际就是将其坐标分别乘上一个比例，那么其参数方程就是这样的

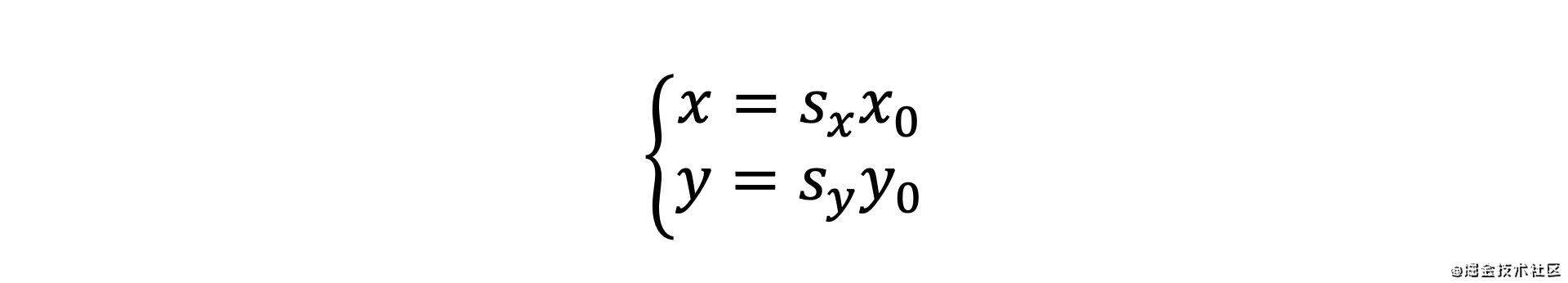
这里可以进行一下拼凑，写成下面这样的形式

Sx*Xo + Sy*0 = x;
Sx*0 + Sy*Yo = y;

根据行列式就可以变成矩阵形式的乘法

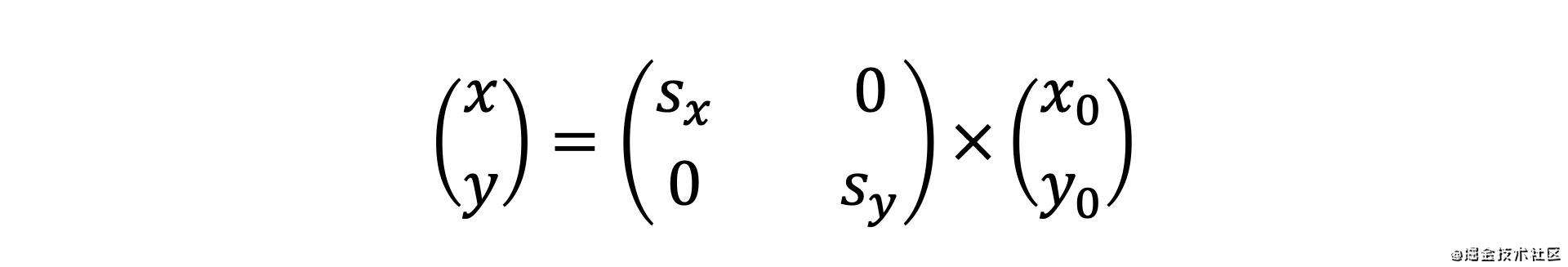
这样等式右边的第一个矩阵就是我们的缩放矩阵了，当然这里是一个二维的缩放矩阵，如果是三维的话，也是这么去推导

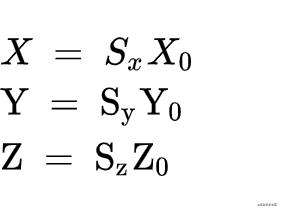
可以看到多了一个Z坐标，按照上面的推导，可以知道，三维情况下的缩放矩阵是这样的

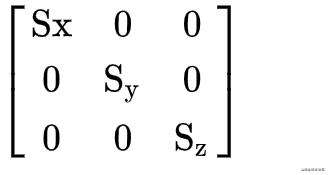
这样就得到了一个三维的缩放矩阵了。下面说到旋转变换也是一样的。

旋转矩阵

计算旋转后的坐标稍微复杂一点，我们来看看如何计算

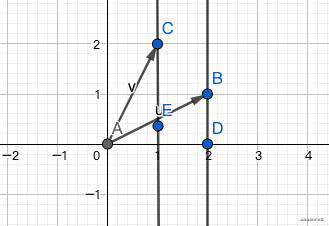
根据上图，假设角BAD为α，旋转的角度为θ，那么可以得到向量v，也就是C点的坐标

C = (|v|cos(α+θ), |v|sin(α+θ))
// 根据两角和公式可得
C = (|v|cosαcosθ - |v|sinαsinθ, |v|cosαsinθ + sinαcosθ)

那么就得到了下面这样的参数方程

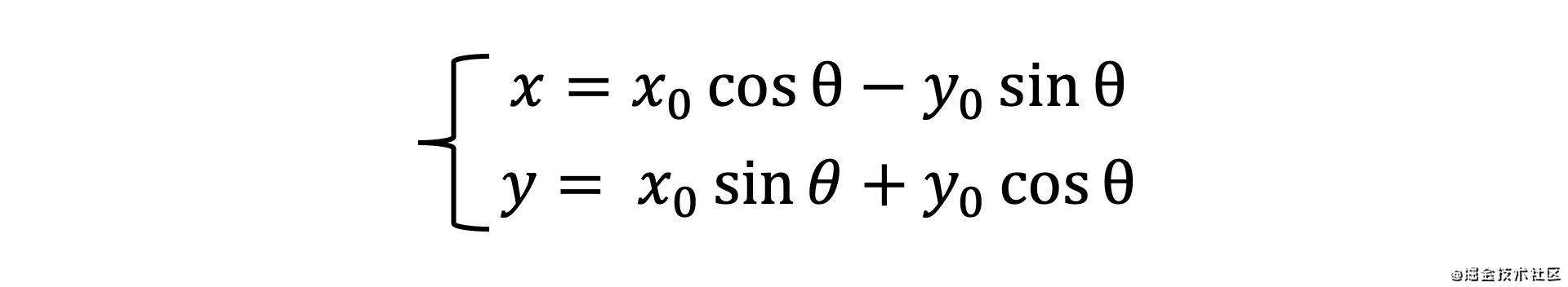
再转化成矩阵形式

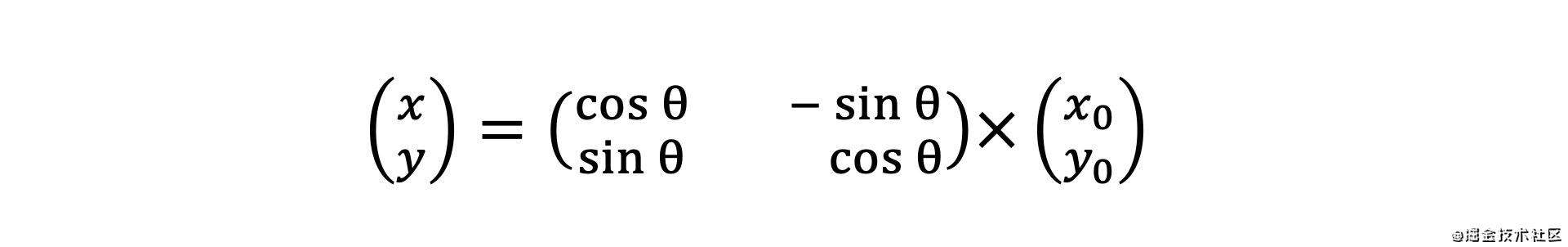
在二维空间中，一般是绕z轴进行旋转，也存在绕x或y轴旋转，不过逻辑都是一样的，绕哪一条轴旋转，那么那个轴的坐标就不变，这里我们还是以绕z轴做示例，所以二维平面中，z的坐标不变，于是可以得到一个3X3的旋转矩阵。

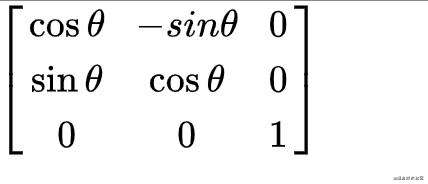
以上两种都叫做线性变换，因为坐标变化都是存在线性关系的，而下面的平移变换则是没有这种关系

平移矩阵

平移很简单，假设空间中存在某个向量a(x0, y0)，我们需要分别沿x轴和y轴方向进行平移x1和y2距离，很容易得到下面的计算：

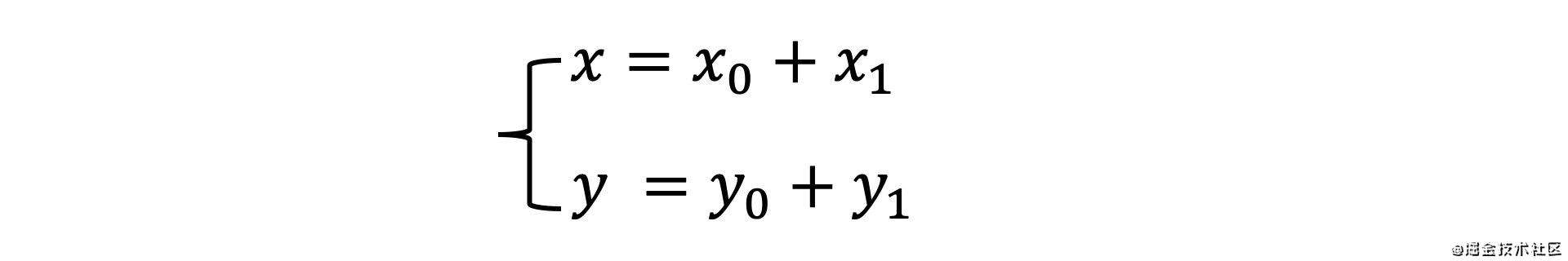
但是由于平移无法写成M*X这样的线性表示，也就无法写出一个3X3的矩阵，为了让变换保持一致，所以又添加了一个维度，使之变成了4X4的矩阵，把最后一个维度设置为1，于是我们来改写一下上面的平移方法

x = ax + by + cz + Tx;
y = dx + ey + fz + Ty;
z = gx + hy + iz + Tz;
1 = jx + ky + mz + p;

首先很容易推导最后一个式子，j、k、m都为0，p为1，同理，x、y、z要变成类似x + x1这样的形式，a、b、c、d、e、f、g、h、i都为0才可以，这样的话，就得到了最后的矩阵表示

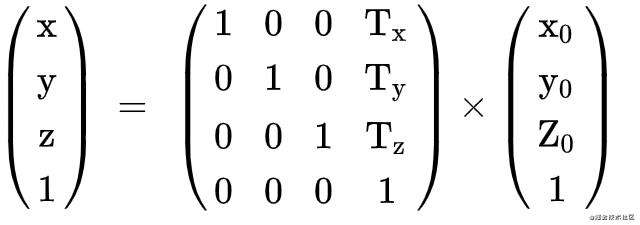
这种添加了一个1的坐标就叫做齐次坐标，得到的矩阵就是齐次矩阵。

为了保持一致，上面的三维变换矩阵都可以改写成齐次矩阵，就是将对角线的地方改为1，其他地方补0就可以了，这里就不展示出来了。

尾声

到这里关于初步用到的图形学的数学知识就差不多了，更详细的可以去下面的资料里面学习了。关于本篇的WebGL的一个例子，有兴趣可以自己动手实现一下。

因为笔者也是初学，难免有错误的地方，也欢迎指正。

地址

参考资料

• 现代计算机图形学入门
• 跟月影学可视化
• WebGL编程指南
• TypeScript图形渲染实战