乘风破浪的WebGL系列-仿射变换数学基础

本文作者：

前言

向量的基本仿射变换分为平移、缩放和旋转。在学习如何使用 WebGL 绘制 3D 形体前，我们需要学习如何对物体进行仿射变换，比如要看到 3D 物体的不同侧面我们需要学习如何对其进行旋转（只看正面看不出立体效果），另外我们要想添加多个方向或者位置不同的 3D 形体时，不需要重复计算每个形体的顶点，而是可以通过对同一形体进行各种各样的仿射变换来实现。所以，让我们学习和回顾仿射变换的基础数学知识——向量和矩阵吧。

本系列其它链接：

• 乘风破浪的WebGL系列-初识WebGL
• 乘风破浪的WebGL系列-着色器语言基础

向量

向量是既有大小，又有方向的量，在物理和工程学中又称为矢量。与之对应的是标量，标量只有大小，没有方向。如身高、体重等。在GLSL 着色器语言中我们可以使用 vec2、vec3、vec4 和 ivec2、ivec3、ivec4 等来表示不同维度、不同数据类型的向量，如 vec3(x, y, z) 表示数据类型为 float 的三维向量。

向量与标量的运算

向量与标量不能相加减，但可以相乘除。向量与向量进行相乘或者相除，需要将向量的每一个元素都与该标量进行相应的运算。向量乘以标量 n 的意义是向量的长度缩放 n 倍。例如向量 乘 3：

向量的加减法

向量与向量的加减法可以被定义为是向量分量的相加或相减，即将一个向量中的每一个分量加上或减去另一个向量的对应分量。例如向量 加向量 为：

向量加法的几何意义是，将两个向量首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。

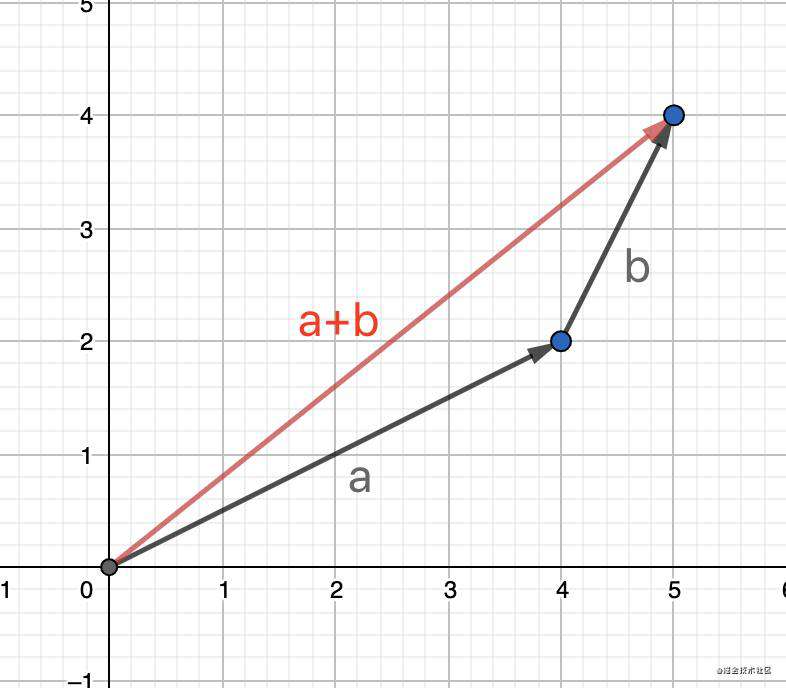
向量减法的几何意义是，将两个向量平移至公共起点，以向量的两条边作平行四边形，结果由减向量的终点指向被减向量的终点。

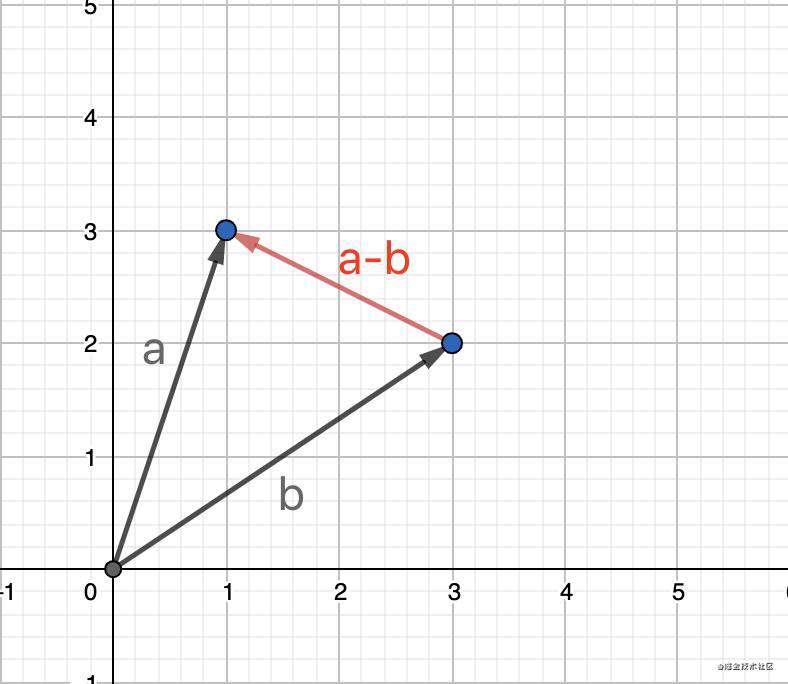
两个向量相等需要满足大小相等和方向相同。

 和 得到的向量是大小和方向相同的，因此可以说向量加法满足交换律；而 和  得到的向量是大小相同但方向相反，因此说向量减法不满足交换律。

向量的乘法

向量乘法有两种，一种是点乘（Dot Product），一种是叉乘（Cross Product）。

点乘

1.点乘的代数定义
设二维空间内有两个向量和 ，定义它们的点乘为以下实数：



2.点乘的几何定义
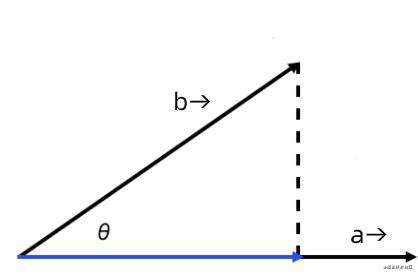
设二维空间内有两个向量 和，和  表示向量的大小，两者间的夹角为 θ，则点乘的几何定义如下：



即  乘以  在  上的投影分量 。

3.点乘的作用
点乘可以用来计算两个向量间的夹角。结合上面两条公式，可以推出 ，再利用反余弦函数 即可获得夹角值。点乘在计算光照的时候非常有用，比如在聚光灯的效果计算中，可以根据点乘来得到光照效果，如果点乘越大，说明夹角越小，则物体离光照的轴线越近，光照越强。在 GLSL 中内置了点乘函数dot(v1, v2)。

叉乘

1.叉乘的数学计算
和点乘不同的是，叉乘的结果不是标量，而是方向与相叉乘的两个向量组成的平面垂直的向量。定义两个三维向量  和 , 和  的叉乘可以表示为如下的行列式：



其中，i、j、k 分别是 x、y、z 轴的单位向量。利用特定公式对其进行展开，如下：



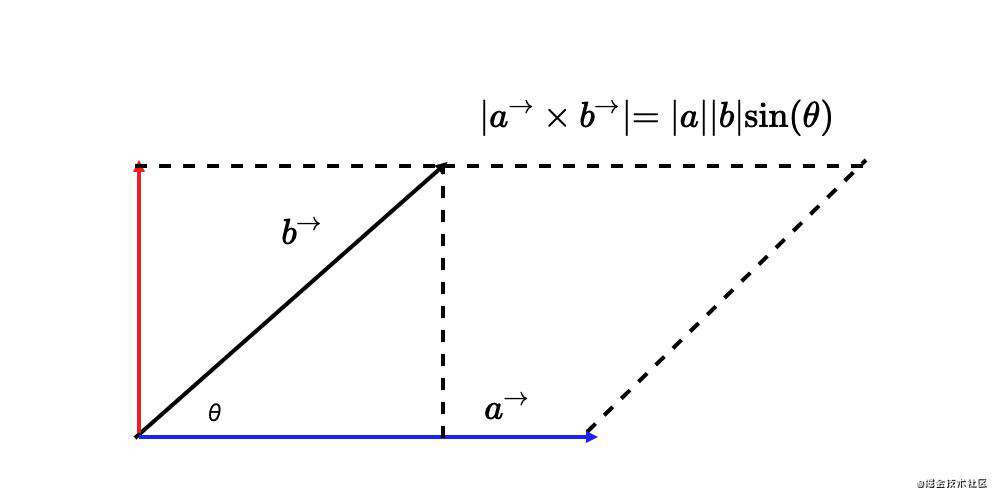
2.叉乘的几何定义
 和 的叉乘的几何含义是，和 组成的平行四边形的面积。

3.叉乘的作用
叉乘同样可以用来计算向量的夹角，结合上面两条公式，可以求出 ，再利用反正弦函数  即可获取夹角值。叉积还可以被运用在求解物体表面法向量。GLSL 中内置了叉乘函数 cross(v1, v2)。

矩阵

矩阵是按照行列排列的一系列数值的集合，一个矩阵通常是由 m 行 n 列组成，我们称之为m x n 矩阵。在 GLSL 着色器语言中我们可以使用 mat2、mat3、mat2x3、mat3x4 等来表示不同行列数的矩阵，如 mat3 表示行列数为 3x3 的矩阵。

矩阵的加减法

矩阵与标量的加减法，需要将标量值加或减到矩阵的每一个元素上。

矩阵相乘

矩阵与标量的乘法和矩阵与标量的加减法一样，矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。

矩阵与矩阵相乘，需要满足左侧矩阵的列数与右侧矩阵的行数相等。结果矩阵的行数为左侧矩阵的行数，列数等于右侧矩阵的列数。

其中，结果矩阵的第一行第一个值为左边第一行和右边第一列的乘积，依此类推。

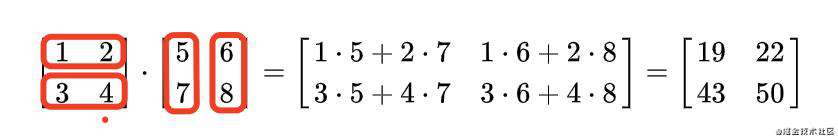
矩阵与仿射变换

仿射变换是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。仿射变换具有以下两个特性：

1. 仿射变换前是直线段的，仿射变换后依然是直线段
2. 对两条直线段 a 和 b 应用同样的仿射变换，变换前后线段长度比例保持不变

对于线性变换，指的是从一个向量空间 v 到另一个向量空间 w 的映射且保持加法运算和数量乘法运算。线性变换除了具有仿射的那两个特性外，还包括以下两个特性：

1. 线性变换不改变坐标原点
2. 线性变换可以叠加，多个线性变换的叠加结果就是将线性变换的矩阵依次相乘，再与原始向量相乘

缩放和旋转等变换都属于线性变换，而由第一条特性可以知道，平移不属于线性变换。

了解了什么是仿射变换后，让我们来看看仿射变换中常用的平移、缩放和旋转是如何计算的吧。

平移

平移是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，我们可以使用向量加法得出平移后的向量：

如果使用 3×3 的矩阵，我们无法定义一个三维的空间的平移矩阵，后面我们会讲到使用齐次坐标定义平移矩阵。

缩放

对一个向量进行缩放就是对向量的长度进行缩放，且保持它的方向不变。在三维空间中进行缩放就是分别对 x、y 和 z 轴进行缩放。我们构造一个缩放矩阵，使得缩放矩阵乘以向量后，向量的每一个分量都能乘以一个缩放因子。

注意这里矩阵和向量的位置不能互换，不然结果就是一个 4 x 4 的矩阵了，而不是一个向量。

旋转

上面两种变换的计算相对容易理解，但旋转稍微复杂些，特别是在三维空间中，物体可以沿着 x、y 和 z 轴旋转。二维的旋转仅能在平面上进行顺时针或逆时针旋转，因此相对简单点，所以让我们从二维旋转学起吧。

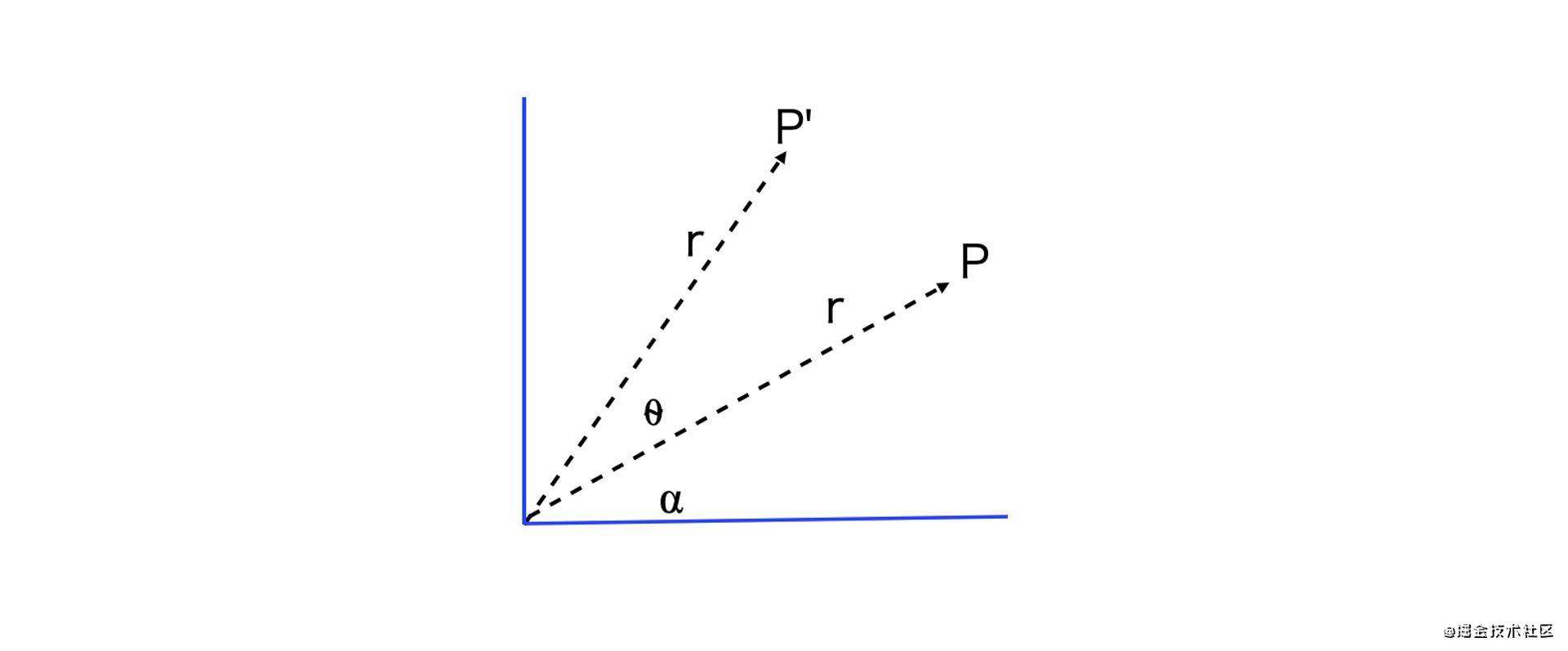
假设向量 P 的长度为 r，角度是 ⍺，将它逆时针旋转 ⍬ 角，推导旋转后的向量 P’ (x, y) 的参数方程为：

写成如下矩阵形式，其中

为一个旋转矩阵。

知道了二维空间中旋转矩阵的推导后，我们延伸到三维空间。在三维空间中，物体可以沿着 x、y 和 z 轴旋转，如下图所示：

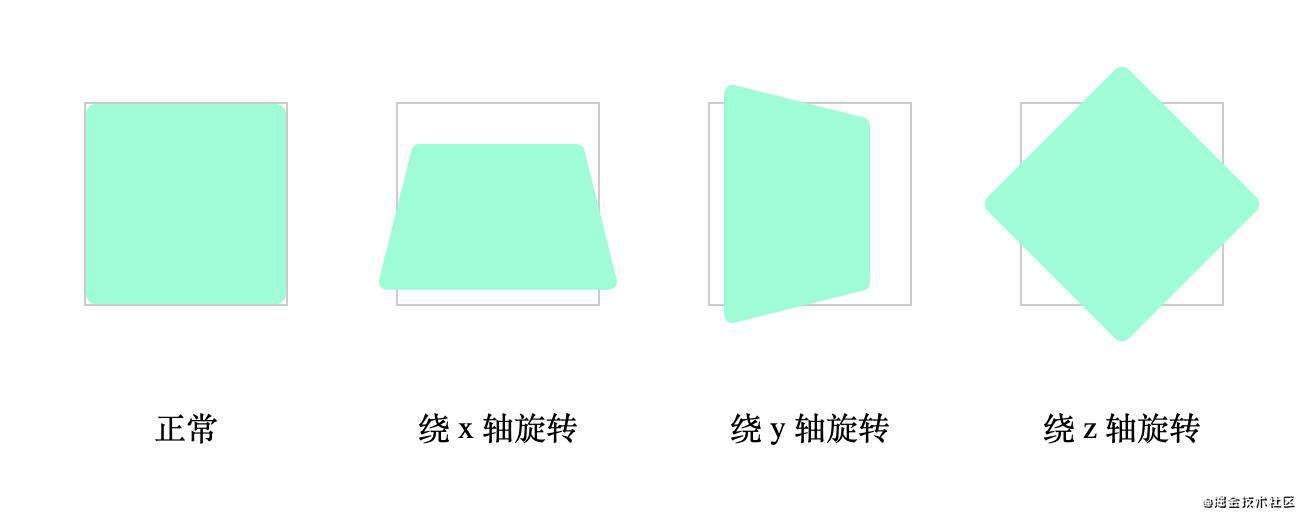
从上图可以看到二维空间的旋转跟三维空间沿 z 轴方向旋转的效果是一样的，x 和 y 轴旋转，z 轴保持不变

沿 x 轴旋转为，x 轴保持不变：

沿 y 轴旋转为，y 轴保持不变：

齐次坐标

根据上面的讨论，我们可以得出，对一个向量 平移、旋转缩放 A 的仿射变换的一般公式为：

当然，这个表达式还可以进一步优化，我们还可以将平移变换也变成矩阵的形式，如何做呢？我们将原本 n 维的坐标转换为 n+1 维的坐标。这种 n+1 维坐标被称为齐次坐标，对应的矩阵就被称为齐次矩阵。使用齐次坐标后，平移矩阵如下表示：

对于缩放和旋转只要保证新增的那一维 w为 1 即可，如下是齐次坐标下的旋转矩阵：

因此在齐次坐标下，对一个向量 平移 、旋转缩放 A 的仿射变换的一般公式为：

矩阵的组合

使用矩阵来表示仿射变换，根据矩阵乘法，我们可以将多个变换组合到一个矩阵中。假设我们有一个顶点 (x, y, z)，我们希望将其缩放 2 倍，然后位移 (1, 2, 3) 个单位。我们需要一个位移和缩放矩阵来完成这些变换。由于矩阵乘法不遵守交换律，当矩阵相乘时，最右边的矩阵是第一个与向量相乘的，在组合矩阵时，一般先进行缩放，然后是旋转，最后才是位移，否则它们会互相影响。最终我们的变换矩阵看起来是这样：

总结

到此我们学习完了向量和矩阵的一些基础知识，为我们后面实现一些复杂的效果打下了基础。回顾本节内容，一开始我们学习了向量的基本运算，然后重点学习了向量的点乘和叉乘，因为这两种运算在图形学中有很多的应用。关于矩阵，我们也学习了一些基础运算，然后重点学习了矩阵和仿射变换，推导出了平移、缩放和旋转矩阵，并介绍了这几种旋转矩阵在齐次坐标下的表示形式。学完了这些基础知识，我们就可以进入 3D 绘图的世界啦。

参考资料：

1. LearnOpenGL教程 变换
2. 掘金小册《WebGL 入门与实践》数学基础：点、向量、矩阵
3. 极客时间《跟月影学可视化》如何用仿射变换对几何图形进行坐标变换