【十天自制软渲染器】DAY 04：Z-buffering

在第三天的学习中，我们学会了如何利用重心坐标算法画三角形，并运用三角形绘制算法把人头模型画了出来。虽然最后的渲染结果能看出来这是个脑袋，但是嘴巴处有很明显的穿帮。这一天我们就学习一下，如何利用 Z-buffering（深度缓冲）来解决层叠问题。

1.画家算法

在正式讲解 Z-buffering 问题之前，我们先来了解一下画家算法。这个算法的思想极其简单，我们可以结合下图简单分析一下：

如果要画一个有山有草有树林的风景画，一个初学者画家可以按以下绘制顺序画画：

首先画最远处的山
然后画次远处的草原
最后画最近的树木

或者我们用更程序员的方式描述一下：

首先画 z-index=1 处的山
然后画 z-index=2 处的草原
最后画 z-index=3 的树木

在现代主流的 UI 渲染引擎中，各个元素的先后层级顺序基本上都是用「画家算法」这种思路决定的：

网页通过 CSS 的 z-index 控制层级顺序
iOS 通过 layer.zPosition 控制层级顺序
Android 通过 index 控制层级顺序

平常画 UI 时，我们可以简单粗暴的把各个 View 理解为一个一个的二维盒子，每个盒子在 z 轴上都是互相独立的，这样我们就可以方便的用 z-index 动态控制盒子的层级；但是在渲染三维物体时，三维模型在 z 轴上是连续的，并且三维模型间还会互相组合交错，这种通过 z-index 控制层级的方案很难奏效。

举个最简单的例子，下图中三个互相交错的三角形，只使用 z-index 是无法区分层级的，更不要说绘制了：

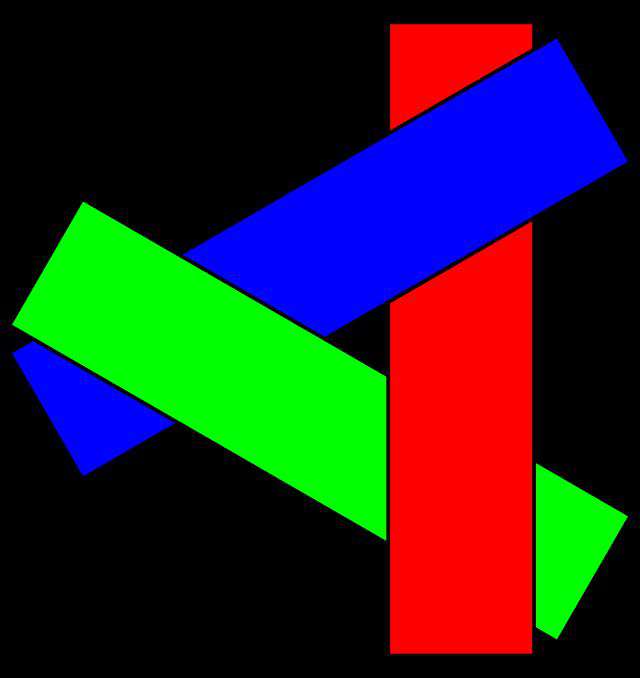
【十天自制软渲染器】DAY 04：Z-buffering

为了解决这个问题，2020 年获得「图灵奖」的计算机图形学大佬——艾德文·卡特姆，提出了一个著名的算法——Z-buffering。

2.Z-buffering

Z-buffering，中文名又为「深度图」「深度缓冲」，它是通过记录比较每个像素的深度信息来解决层级问题。

Z-buffering 算法理解起来其实是非常直观的，我们这里借用《虎书 4》里的一张插图（可以关注?️号「卤蛋实验室」后台回复「图形学」领取本书）来讲解一下 Z-buffering 的工作原理。

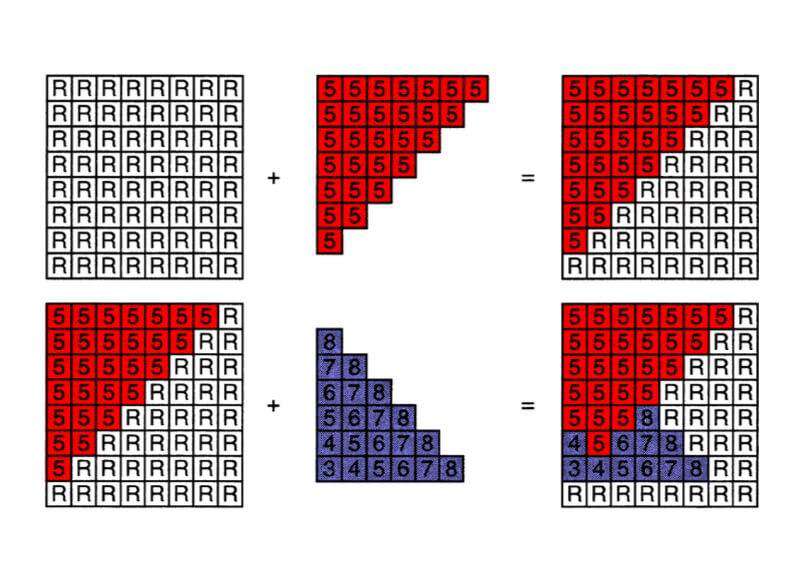
【十天自制软渲染器】DAY 04：Z-buffering

首先我们假设要在一个 8*8 的屏幕上渲染两个互相遮挡的三角形，我们在正式渲染前先开辟一块儿 8*8 的二维内存空间，这个空间的默认值均为 -∞。

假设我们已知两个三角形的每个像素的深度信息，红三角形的深度均为 5，紫三角形的深度区间为 [3, 8]。

我们先遍历红色三角形的所有像素，和 Z-buffering 的默认值 -∞ 比较，哪个值大，就保留哪个值。经过第一轮比较后，我们就记录了红色三角形的深度信息。

然后我们遍历紫色三角形的所有像素。和最新的 Z-buffering 逐像素比较，哪个值大，就保留哪个值。第二轮比较后我们就又记录了紫色三角形的深度信息。

最后我们就得到了一份深度缓冲，它记录了这张图片的层级顺序，最终渲染时我们按这个深度缓冲逐像素渲染三角形即可。

上面的思路写成伪代码就是这样的：

// 首先假设深度默认值都是负无穷 -∞(这里可以是无穷大，也可以是无穷小，依坐标系而定)
for (each triangle T)              // 遍历每个三角形
   for (each sample (x,y,z) in T)  // 遍历三角形里的每个像素
        if (z > zbuffer[x,y])        // 如果深度大于已有的值，
            framebuffer[x,y] = rgb;  // 则更新颜色，
            zbuffer[x,y] = z;        // 并更新 zbuffer
        else
            // do nothing            // 小于已有的值，就说明这个像素点被遮挡不需要绘制了

3.代码实现

理解了上面的伪代码，现成真正的代码就很容易了。

首先我们定义一下 Z-buffering 的数据结构。按道理来说，我们直接定义成一个二维数组是最符合渲染场景的，第一维表示列，第二维表示行：

// [[1, 2, 3],
//  [4, 5, 6],
//  [7, 8, 9]]

但是我们并不需要这样写，我们可以把二维数组拍平，然后通过偏移量进行访问（可以联想一下循环队列和最大堆这两种数据结构的底层实现）：

// [[1, 2, 3],       [1, 2, 3,
//  [4, 5, 6],   =>   4, 5, 6,
//  [7, 8, 9]]        7, 8, 9],

定义好结构后，我们给 Z-buffering 的每个子元素都赋上 -∞ 的默认值：

float *zbuffer = new float[width * height];

for (int i=0; i < width * height; i++) {
    zbuffer[i] = -std::numeric_limits<float>::max();
}

最后把上面的伪代码翻译为正常的 cpp 代码就可以了：

//......

Vec3f P;
for (P.x = boxmin.x; P.x <= boxmax.x; P.x++) {
    for (P.y = boxmin.y; P.y <= boxmax.y; P.y++) {
        Vec3f bc_screen = barycentric(pts, P); // bc 是 Barycentric Coordinates 的缩写

        //......
        
        // 计算当前像素的 zbuffer
        P.z = 0;
        for (int i = 0; i < 3; i++) {
            P.z += pts[i][2] * bc_screen[i];
        }
        
        // 更新总的 zbuffer 并绘制
        if(zbuffer[int(P.x + P.y * width)] < P.z) {
            zbuffer[int(P.x + P.y * width)] = P.z;
            image.set(P.x, P.y, color);
        }
    }
}

//......

加入 Z-buffering 计算后，我们渲染的模型就完全正常了：

【十天自制软渲染器】DAY 04：Z-buffering

相应的，如果把 Z-buffering 渲染为一张图，则是下面这样的：

【十天自制软渲染器】DAY 04：Z-buffering

个人认为 Z-buffering 的概念还是很简单的，理论了解清楚后代码很容易写出来。在实际应用中，Z-buffering 其实还有很多的问题，例如因为精度问题引起的 z-fighting，相应的也有一些解决方案。因为本系列教程目标只是构建一个最小功能的软渲染器，这些相对深入的问题就不探讨了，感兴趣的同学可以自行搜索学习。

欢迎大家关注我的微信公众号：卤蛋实验室，目前专注前端技术，对图形学也有一些微小研究。

原文链接 ? day04-Z-buffering：更新更及时，阅读体验更佳