利用神经网络实现多元线性回归预测方案

相关概念

机器学习

机器学习（Machine Learning，ML）：是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。其专门研究计算机是怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构，使之不断改善自身的性能。

监督式学习：在监督式学习下，输人数据被称为“训练数据”，每组训练数据都有一个明确的标识或结果。在建立预测模型的时候，监督式学习建立一个学习过程，将预测结果与“训练数据”的实际结果进行比较，不断地调整预测模型，直到模型的预测结果达到一个预期的准确率。监督式学习的常见应用场景包括分类问题和回归问题。常见算法有逻辑回归（Logistic Regression）和反向传递神经网络（Back Propagation Neural Network)。

非监督式学习：在非监督式学习下，数据并不被特别标识，学习模型是为了推断出数据的一些内在结构。常见的应用场景包括关联规则的学习及聚类等。常见算法包括Apriori算法和K-Means算法。

半监督式学习：在半监督式学习下，输人数据部分被标识，部分没有被标识。这种学习模型可以用来进行预测，但是模型首先需要学习数据的内在结构，以便合理地组织数据进行预测。其应用场景包括分类和回归。常见算法包括一些对常用监督式学习算法的延伸。这些算法首先试图对未标识的数据进行建模，然后在此基础上对标识的数据进行预测，如图论推理算法（Graph Inference）或拉普拉斯支持向量机（Laplacian SVM）等。

强化学习：在强化学习下，输人数据作为对模型的反馈，不像监督模型那样，输入数据仅仅作为一种检查模型对错的方式。在强化学习下，输入数据直接反馈到模型，模型必须对此立刻做出调整。常见的应用场景包括动态系统及机器人控制等。常见算法包括Q-Learning及时间差学习（Temporal Difference Leaming）等。

回归算法：回归算法是试图采用对误差的衡量来探索变量之间的关系的一类算法。

TFJS

• 张量（tensors）：TFJS是在JavaScript中使用张量来定义并运行计算的框架，它是一个形状为一维或多维数组组成的数值的集合。
• WebGL：浏览器平台中的3D绘图标准，用来实现张量的存储和数学操作。
• 模型（models）：机器学习中，一个model是一个带有可训练参数的函数。这个函数将输入转化为输出。
• 损失函数（losses）：模型将以最小化损失作为目标。该函数旨在将模型预测的“误差程度”量化为具体数字。
• 优化器（optimizers）：优化器的作用是在给定当前模型预测的情况下，决定对模型中每个参数实施更改的幅度。
• 指标列表（metrics）：与损失类似，指标也会计算一个数字，用于总结模型的运作情况。通常要在每个周期结束时基于整体数据来计算指标。

统计学

• 均方误差（mean-square error，MSE）：是反映估计量与被估计量之间差异程度的一种度量。

WHY（目的、 理念）

基于结构性归因和相关性分析的输入数据进行机器学习训练、预测，输出线性回归数据和可视化图表。

HOW（方法、措施）​

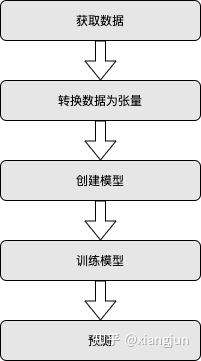
机器学习方案

​一、创建模型

// 构造一个线性回归模型
function createModel(numOfFeatures) {
  // 通过tf.sequential()工厂函数创建Sequential模型
  const model = tf.sequential();
  // 输入层
  // 定义inputShape定义为1
  // units设置权重矩阵在层中的大小。通过将它设为1，意味着数据的每个输入特征都有一个权重
  model.add(tf.layers.dense({ inputShape: [numOfFeatures], units: 1 }));
  // 输出层
  // units设置为1，意味着输出一个数据
  model.add(tf.layers.dense({ units: 1 }));

  return model;
}

二、准备数据，将数据转换为张量

归一化公式：

function convertToTensor(data) {
  return tf.tidy(() => {
    // 获取因变量
    const inputs = data.x;
    // 获取自变量
    const labels = data.y;
    
    // 转换数组数据为2d张量
    // e.g. input: [1,2,3]
    // output: [[1], [2], [3]]
    const inputTensor = tf.tensor2d(inputs);
    const labelTensor = tf.tensor2d(labels, [labels.length, 1]);

    // 将数据归一化，解决大数据计算的问题
    const inputMax = inputTensor.max();
    const inputMin = inputTensor.min();
    const labelMax = labelTensor.max();
    const labelMin = labelTensor.min();

    const normalizedInputs = inputTensor
      .sub(inputMin)
      .div(inputMax.sub(inputMin));
    const normalizedLabels = labelTensor
      .sub(labelMin)
      .div(labelMax.sub(labelMin));

    return {
      inputs: normalizedInputs,
      labels: normalizedLabels,
      inputMax,
      inputMin,
      labelMax,
      labelMin,
    };
  });
}

三、训练模型

输入张量x映射到输出张量y通过等式 来描述，其中_kernel_和_bias_为dense层可调参数。它们的值是在创建模型时是随机选择的，这些随机值不能很好地预测。为了进行更准确的预测，我们必须通过模型从数据中学习来寻找更好的_kernel_值和偏差值。这个搜索就是训练过程。

function trainModel(model, inputs, labels) {
  return new Promise((resolve, reject) => {
    model.compile({
      optimizer: 'sgd',
      loss: 'meanAbsoluteError',
      metrics: ['mse'],
    });

    const batchSize = 32; // 批处理大小
    const epochs = 200; // 训练次数

    return model
      .fit(inputs, labels, {
        batchSize,
        epochs,
        callbacks: { onEpochEnd: (epoch, logs) => console.log(logs) },
      })
      .then(res => {
        resolve(res);
      })
      .catch(err => {
        reject(err);
      });
  });
}

四、预测

function predict(model, inputData, normalizationData) {
  const { inputMax, inputMin, labelMin, labelMax } = normalizationData;

  const arr = tf.tidy(() => {
    // 创建100个新示例来提供给模型
    const xs = tf.linspace(0, 1, 100);
    // 通过reshape将1d张量转换为2d张量
    const preds = model.predict(xs.reshape([100, 1]));
    // 将数据转换为原始的值
    const unNormXs = xs.mul(inputMax.sub(inputMin)).add(inputMin);

    const unNormPreds = preds.mul(labelMax.sub(labelMin)).add(labelMin);

    return [unNormXs.dataSync(), unNormPreds.dataSync()];
  });

  const xs = arr[0];
  const preds = arr[1];

  const predictedPoints = Array.from(xs).map((val, i) => {
    return { x: val, y: preds[i] };
  });

  const originalPoints = inputData.map(d => ({
    x: d.x,
    y: d.y,
  }));

  return {
    predictedPoints,
    originalPoints,
  };
}

可视化效果（一元线性回归为例）

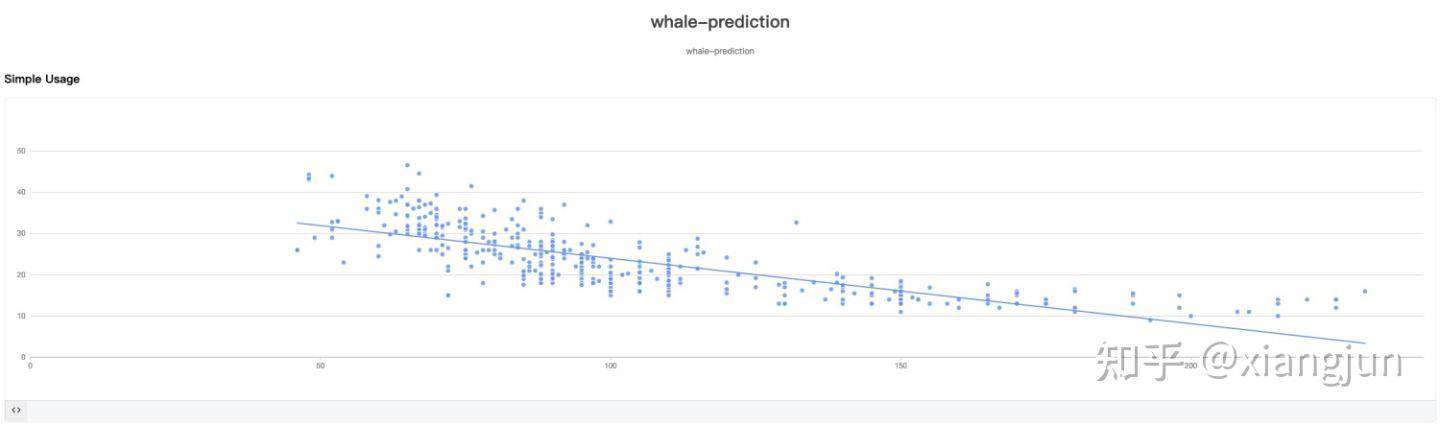
WHAT（现象、成果）

均方误差

均方误差是各数据偏离真实值的距离平方和的平均数。

公式：

对于预测结果的评估方法通过计算损失函数的loss值与手动计算的均方误差进行对比得出，其中loss值比手动计算的均方误差越低表示预测结果越精准。

function evaluate(inputs, labels) {
  const result = labels.sub(inputs).pow([2]).mean();
  result.print();
  return result;
}

评估结果

通过手动计算的均方误差约为：0.16，通过配置epochs为200训练之后loss值为：0.017，这表示预测是数据比手动计算的精度高出多倍。

参考

《深度学习之Javascript》:  [https://wendydesigner.github.io/DLwithjs---chinese/

](link.zhihu.com/?target=htt…)