一、冒泡排序（bubbleSort)

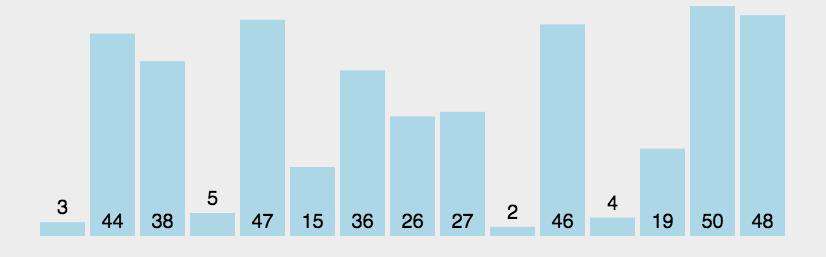
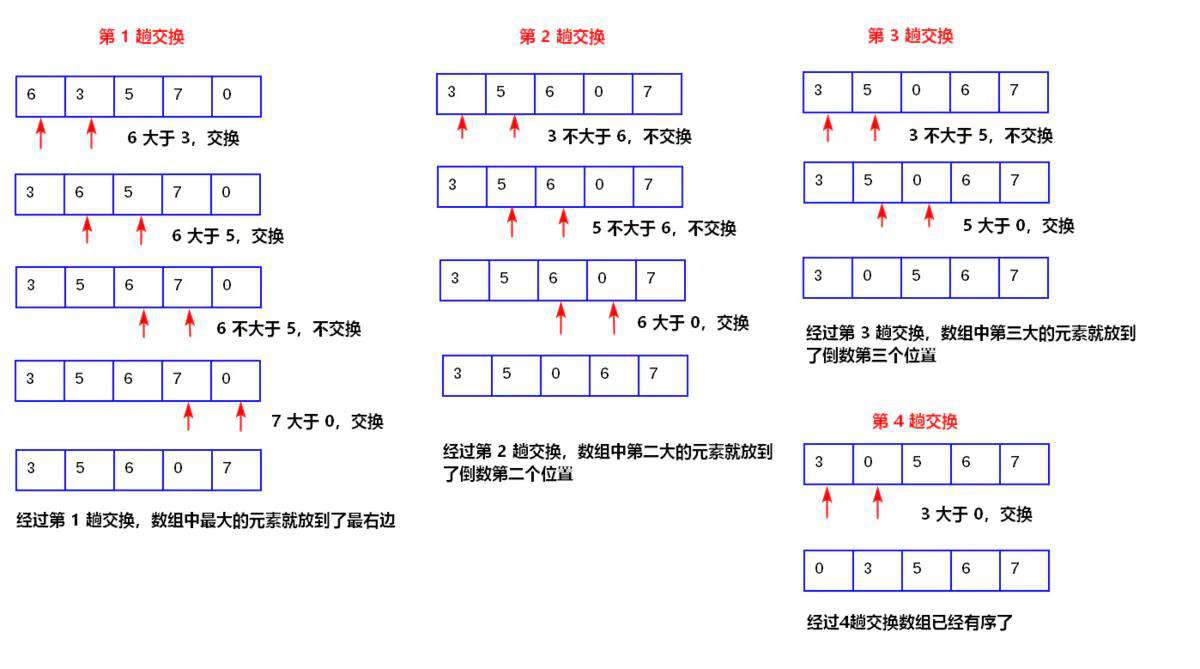
• 比较所有相邻元素，如果第一个比第二个大，则交换它们的位置
• 一轮下来，可以保证最后一个数是最大的
• 执行n-1轮，就可以完成排序

Array.prototype.bubbleSort = function () {
  for (let i = 0; i < this.length - 1; i++) {
    //循环第一次之后数组最后一位就是最大的，下一次循环到最后一位的前i位就行，所有-i,这样每次冒泡排序的区间都会把已排序好的区间减掉
    for (let j = 0; j < this.length - 1 - i; j++) {
      //第一位和第二位比较，如果第一位比第二位大，则交换位置
      if (this[j] > this[j + 1]) {
        const temp = this[j];
        this[j] = this[j + 1];
        this[j + 1] = temp;
      }
    }
  }
  return this;
};
const arr = [5, 4, 3, 2, 1];
console.log(arr.bubbleSort());

function bubbleSort(arr) {
  let length = arr.length;
  for (let i = 0; i < length - 1; i++) {
    //循环第一次之后数组最后一位就是最大的，下一次循环到最后一位的前i位就行，所有-i,这样每次冒泡排序的区间都会把已排序好的区间减掉
    for (let j = 0; j < length - 1 - i; j++) {
      //第一位和第二位比较，如果第一位比第二位大，则交换位置
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
  return arr;
}
const arr = [5, 5, 7, 2, 8, 1, 0, 4, 5, 1];
console.log(bubbleSort(arr));

时间复杂度：O(n^2) 空间复杂度：O(1) 稳定性：冒泡排序是稳定的排序算法，因为可以实现值相等的元素的相对位置不变

二、选择排序（selecttionSore）

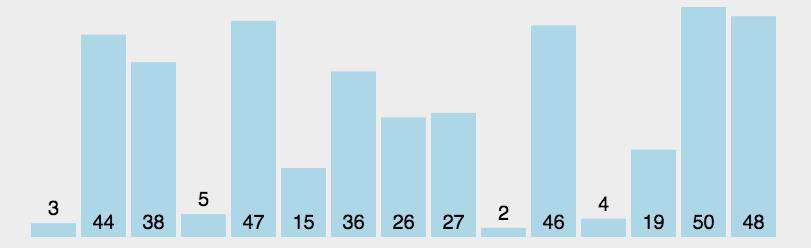
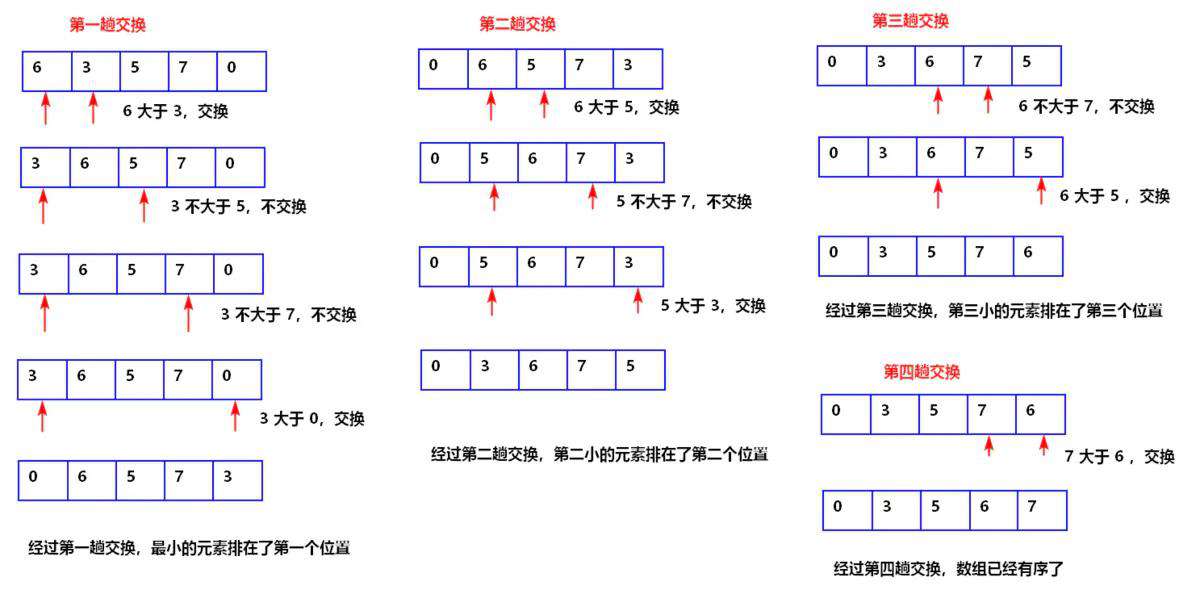
• 找到数组中的最小值，选中它并将它放到第一位。
• 接着找到第二小的值，选中它并将它放到第二位。
• 以此类推，执行n-1轮

Array.prototype.selecttionSore = function() {
  //执行n-1轮之后完成排序
  for (let i = 0; i < this.length - 1; i++) {
    //声明一个最小值下标，默认为0，第一轮为第一个元素，第二轮为第二个元素
    let indexMin = i;
    //做一次循环，如果当前元素小于最小值，那么最小值下标就要换成当前元素下标
    //外层每做一次循环，前面i个元素是已经排好序的，所以排序区间从i开始
    for (let j = i; j < this.length; j++) {
      if (this[j] < this[indexMin]) {
        indexMin = j;
      }
    }
    //经过一轮循环就可以找到最小值的下标
    //将最小值和数组的第一个元素进行交换
    const temp = this[i]; //数组的第一个值
    this[i] = this[indexMin]; //将数组第一个值设为最小值
    this[indexMin] = temp; //将最小值下标元素设为数组第一个值
  }
  return this;
};

const arr = [6, 5, 4, 3, 2, 1];
console.log(arr.selecttionSore());

const arr = [6, 5, 4, 3, 2, 1];
function selectionSort(arr) {
  let length = arr.length;
  for (let i = 0; i < length - 1; i++) {
    let indexMIn = i;
    for (let j = i; j < length; j++) {
      if (arr[j] < arr[indexMIn]) {
        indexMIn = j;
      }
    }
    const temp = arr[i];
    arr[i] = arr[indexMIn];
    arr[indexMIn] = temp;
  }
  return arr;
}

console.log(selectionSort(arr));

时间复杂度：O(n^2) 空间复杂度：O(1) 稳定性：选择排序是不稳定的排序算法，因为无法保证值相等的元素的相对位置不变，例如 [3, 4, 3, 1, 5]这个数组，第一次交换，此时原来两个3的相对位置发生了变化。

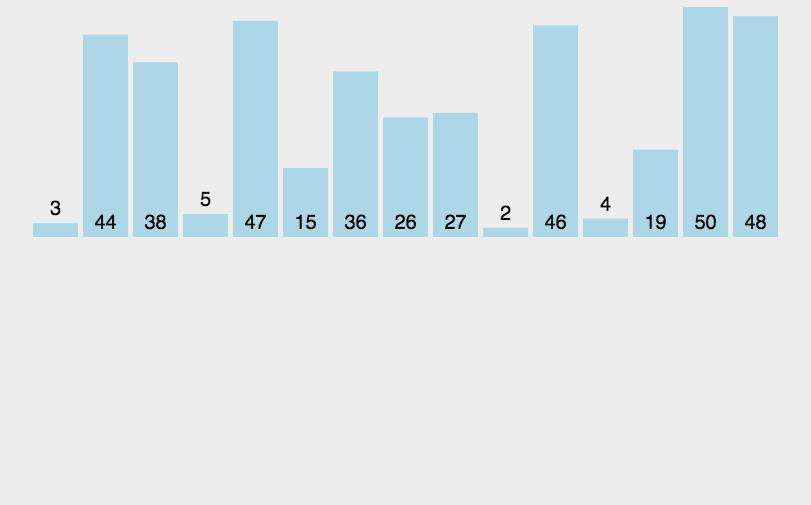
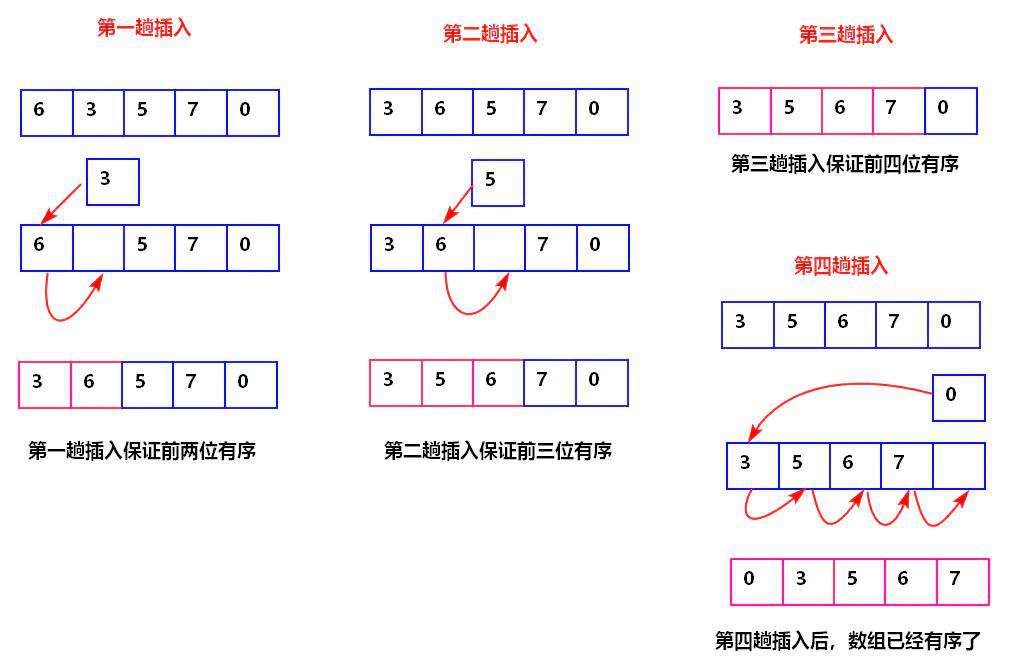
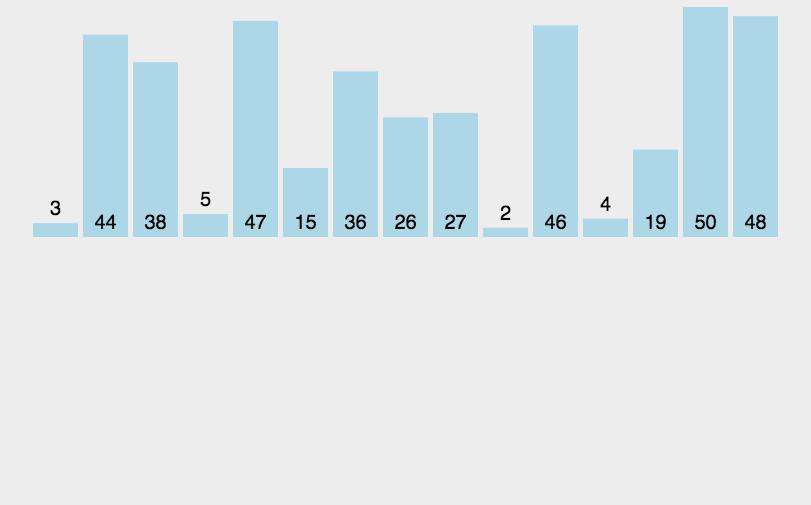
三、插入排序（insertionSort）

• 将数组的左边看作已经排序好的有序序列，每次将一个数字插入该有序序列；
• 从第二个书开始往前比，如果有比它大的就往后排，第二个数比完比第三个数，把第三个数与前面的比较；
• 从排序好的数组最右侧开始比较，若比被比较的数较大，被比较的数后移一位，比较的数插入其中
• 以此类推进行到最后一个数

Array.prototype.insertionSort = function() {
  //从第二个开始循环，所以i=1
  for (let i = 1; i < this.length; i++) {
    let temp = this[i]; //找到右边没排序的第一个数，第一次循环默认为第二个数
    let j = i; //左边已经排序好了的个数
    while (j > 0) {
      //将需要插入的数依次与左边排序好的数组对比
      //如果需要插入的数比被对比的数小，被对比的数往后移一位
      //如果需要插入的数比被比较的数大，则退出
      if (temp < this[j - 1]) {
        this[j] = this[j - 1]; //前面的数往后移一位
      } else {
        break;
      }
      j--;
    }
    //循环结束之后j的值就是要插入的位置，将temp插入进去
    this[j] = temp;
  }

  return this;
};

const arr = [6, 5, 4, 3, 2, 1];
console.log(arr.insertionSort());

const arr = [1, 8, 5, 2, 13, 7, 42, 64, 2];
function insertionSort(arr) {
  //从数组的第二位开始往左比较，所以i=1
  for (let i = 1; i < arr.length; i++) {
    let target = i; //这个是右边没排序的第一个数，第一次循环默认位第二个数
    for (let j = i - 1; j >= 0; j--) {
      //将target与左边排序好的数比较，如果比较小，则与被比较的数交换位置
      if (arr[target] < arr[j]) {
        [arr[target], arr[j]] = [arr[j], arr[target]];
        //交换完之后target往前插入一位
        target = j;
      } else {
        //如果前面没有比target小的数，退出循环
        break;
      }
    }
  }
  return arr;
}

console.log(insertionSort(arr));

第一种思路更符合插入的概念 时间复杂度：O(n^2) 空间复杂度:O(1) 稳定性：插入排序稳定的排序算法，满足条件arr[target] < arr[j]才发生交换，这个条件可以保证值相等的元素的相对位置不变。

四、归并排序（mergeSort）

利用归并的思想实现的排序方法。 该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。（分治法将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

• 分：把数组从中点进行分割，分为左、右两个数组，再递归地对子数组进行”分操作“，直到数组长度小于2，成一个个单独的数
• 合：把两个数合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整数组，如果需要合并，那么左右两数组已经有序了。

创建一个临时存储数组res，比较两数组第一个元素，将较小的元素加入临时数组，如果两个数组还有值的话重复上诉操作， 若左右数组有一个为空，那么此时另一个数组一定大于res中的所有元素，直接将其所有元素加入res

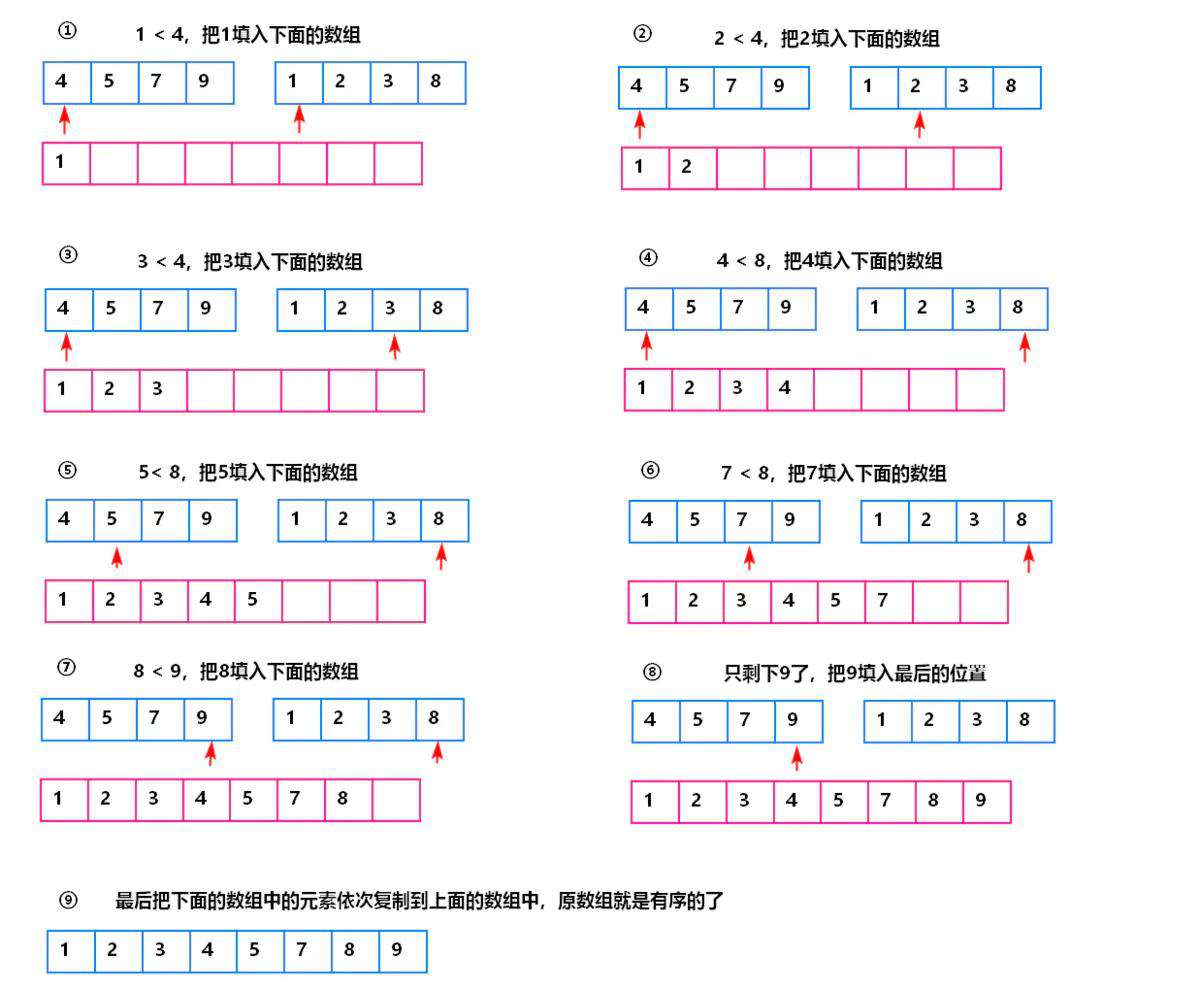
归并排序的流程

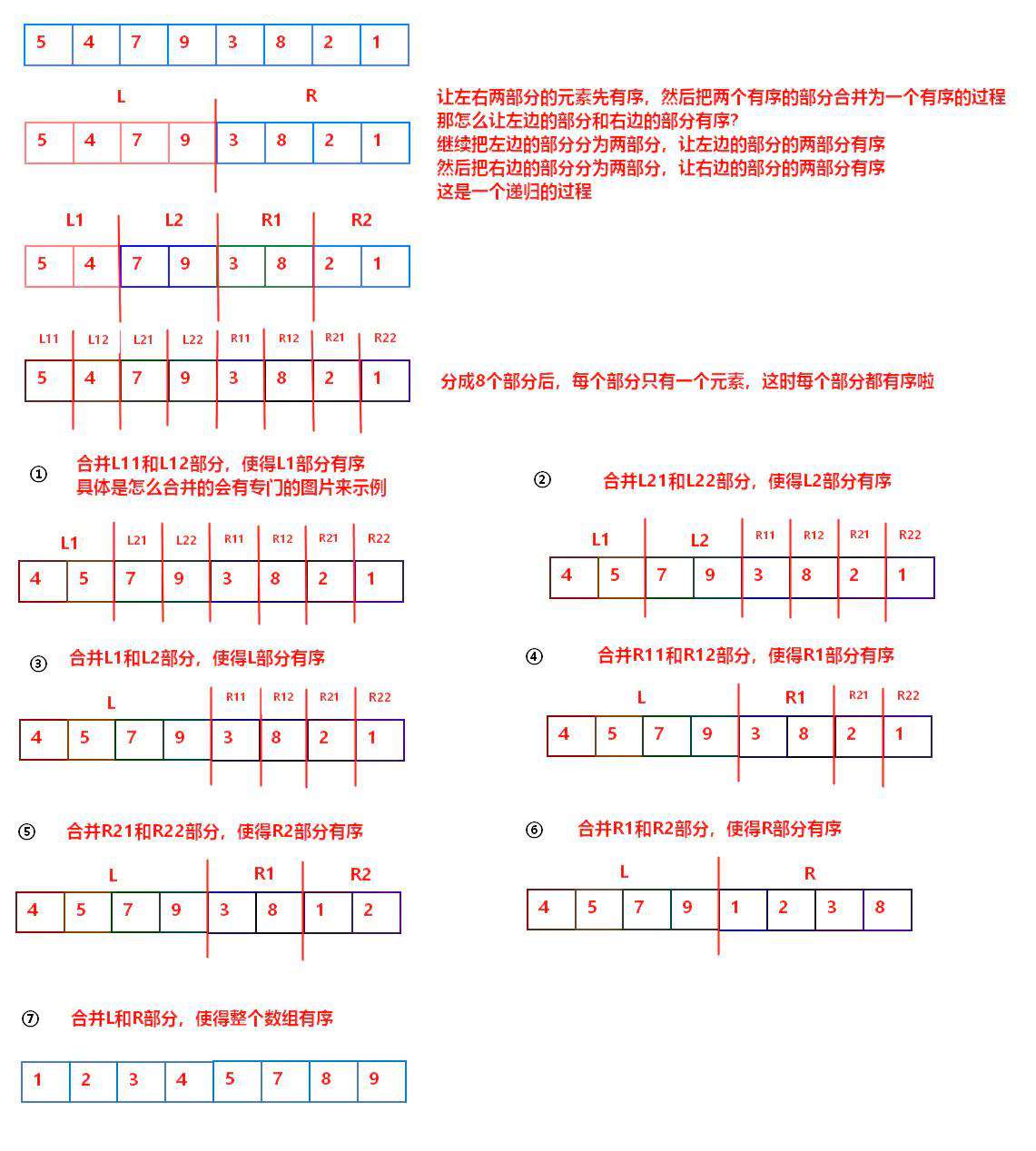
合并两个有序数组的流程

Array.prototype.mergeSort = function () {
  //第一步，分，将数组分为长度小于2的数组，长度小于2代表这个数组已经有序
  const rec = (arr) => {
    if (arr.length < 2) {
      return arr;
    }
    const mid = Math.floor(arr.length / 2); //获取数组中间下标，将数组分为左右两个数组
    const left = arr.slice(0, mid); //左边数组
    const right = arr.slice(mid, arr.length); //右边数组
    //调用递归将左右两边的数组继续拆分，直到数组长度小于2
    const orderLeft = rec(left); //有序的左边数组，最后return出来的长度为1
    const orderRight = rec(right); //有序的右边数组
    const res = [];
    //当左边或者右边数组有值的情况下
    while (orderLeft.length || orderRight.length) {
      //当左边数组和右边数组都有值的情况下，比较左右两边数组的第一个数，将较小的数推入res中
      if (orderLeft.length && orderRight.length) {
        res.push(
          orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift()
        );
      }
      //如果右边数组值为空，左边不为空，将左边的数全部推入res
      else if (orderLeft.length) {
        res.push(orderLeft.shift()); //删除并返回数组的第一个元素
      } else if (orderRight.length) {
        res.push(orderRight.shift());
      }
    }
    //返回合并后的有序数组作为递归的结果
    return res;
  };
  const res = rec(this);
  // console.log(res);
  res.forEach((n, i) => {
    this[i] = n;
  });
  return this;
};
const arr = [5, 8, 4, 3, 2, 1];
console.log(arr.mergeSort());

函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。所以递归调用自身时入栈，函数返回之后出栈 所以归并排序的核心思想就是重复拆分调用自身，在栈顶添加元素，直到数组长度小于2时，开始对栈顶函数进行合并并且返回合并之后的数组

另外一种递归调用

const arr = [9, 8, 7, 6, 5, 4, 3, 2, 1, 0];

function mergeSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const midIndex = Math.floor(arr.length / 2);
  const left = arr.slice(0, midIndex);
  const right = arr.slice(midIndex, arr.length);
  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  let temp = [];
  while (left.length && right.length) {
    temp.push(left[0] < right[0] ? left.shift() : right.shift());
  }
  while (left.length) {
    temp.push(left.shift());
  }
  while (right.length) {
    temp.push(right.shift());
  }
  return temp;
}
console.log(mergeSort(arr));

时间复杂度：O(nlogn)，递归劈成两半logn,循环n次，所以nlogn 空间复杂度:O(n) 稳定性：归并排序是稳定的排序算法

五、快速排序（quickSort）

快速排序也是采用分治思想

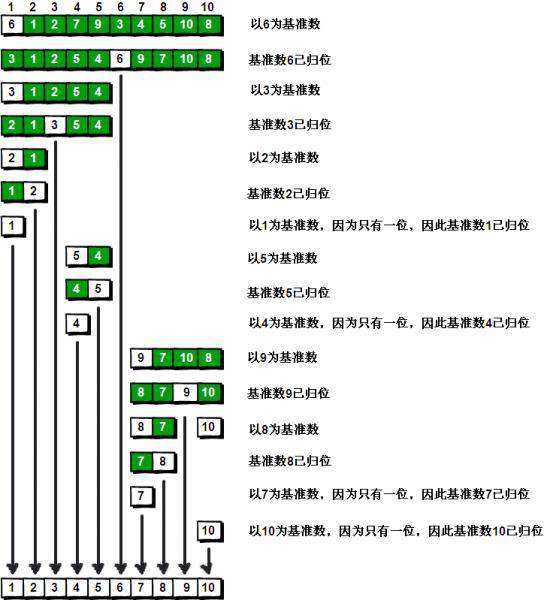
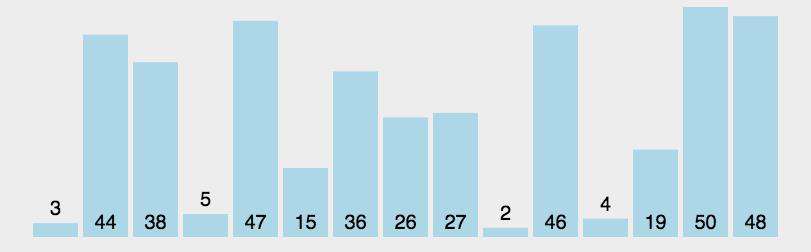
• 分区： 从数组中任意选择一个“基准”（一般选第一个数），所有比基准小的元素放在基准前面，比基准大的元素放在基准后面，此时的基准元素已经找到合适的位置了，基准前面的数都比他小，后面的数都比他大
• 递归：递归地对基准前后的子数组进行分区，这样就可以在子数组中找到一个“基准”将他放在合适的位置，递归到数组的长度小于2，结束递归，等所有的子数组都排序好了，排序完成

Array.prototype.quickSort = function () {
  //递归函数
  const rec = (arr) => {
    //如果元素长度小于2就不需要排序了
    if (arr.length < 2) {
      return arr;
    }
    const left = []; //比基准小的数组
    const right = []; //比基准大的数组
    const mid = arr[0]; //数组的第一位为基准
    //从数组的第二位开始循环与基准进行比较
    for (let i = 1; i < arr.length; i++) {
      //如果比基准小，插入left中，否则插入y中
      if (arr[i] < mid) {
        left.push(arr[i]);
      } else {
        right.push(arr[i]);
      }
    }
    //返回值为左边数组+基准元素+右边数组
    return [...rec(left), mid, ...rec(right)];
  };
  const res = rec(this);
  res.forEach((n, i) => {
    this[i] = n;
  });
  return this;
};
const arr = [9, 4, 9, 21, 56, 1, 74, 8, 98, 2, 97, 0];
console.log(arr.quickSort());

    function quickSort(array) {
      if (array.length < 2) {
        return array;
      }
      const mid = array[0];
      const left = [];
      const right = [];
      for (let i = 1; i < array.length; i++) {
        if (array[i] < mid ) {
          left.push(array[i]);
        } else {
          right.push(array[i]);
        }
      }
       return [...quickSort(left), mid, ...quickSort(right)];
    }

时间复杂度：平均O(nlogn)，最坏O(n2)，实际上大多数情况下小于O(nlogn) 空间复杂度:O(logn)（递归调用消耗） 稳定性：不稳定，无法保证相等的元素的相对位置不变

二分搜索

是一种在有序数组中查找元素的算法

• 从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束，返回中间元素下标值
• 如果目标值大于或者小于中间元素，则在大于或者小于中间元素的那一半数组搜索
• 递归重复第一步直到找到元素，否则返回-1

Array.prototype.binarySearch = function (item) {
  let low = 0; //数组的最小下标
  let high = this.length - 1; //数组的最大下标
  //在最小下标小于最大下标的前提下
  while (low < high) {
    const mid = Math.floor((low + high) / 2);
    const element = this[mid]; //中间元素
    if (element < item) {
      //目标元素在较大的那一半中，最小下边为mid+1
      low = mid + 1;
    } else if (element > item) {
      //目标元素在较小的那一半中，最大下边为mid-1
      high = mid - 1;
    } else {
      return mid;
    }
  }
  return -1;
};

const arr = [1, 2, 3, 4, 5, 6];
console.log(arr.binarySearch(5));