用js写红包
首先确定一下,最小的单位是1分钱 每个人最少1分钱
再来看如果随机均分
先看简单的场景:2个人分10块钱,是不是很简单,第一个人直接随机(0,10),第二个人获得剩下的。
如果是3个人分15呢?第一个人也应该是随机(0,??)问题是这个??应该怎么得。
回顾2人分10元。两人分10元的这个(0,10)是怎么来的呢?这样看,第一个人均分5元,然后为了体现红包的随机性和刺激性,将5向两边扩展,比如(4,6),(3,7)直到(0,10),这种扩展很公平,因为均值是5.
同理,3人分15的时候,第一个人均分为5元,向两边扩展是(0,10)因为0再小就是负数了,好家伙抢个红包还倒贴钱?,他随机分走了x元,问题就变成了剩下的两个人分(15-x)元,那问题就简单了。回顾该过程,3人分钱=1人先公平分走x元 + 2人分(钱-x)。同理,四人分钱就是=1人先公平分走x元 + 3人分(钱-x),因为1人先公平分走x元是公平的,均值为 钱数/人数,而里面的俄罗斯套娃则同理,导致每个人分走的钱都是公平的。
最后一分钱问题
在我实际敲代码的时候,又遇到了一个问题,上面的2人分10元是10/2除的尽,如果3人分0.04元呢?调入公式,人傻了,[0,0.02/3),最小单位却是0.01,你难道四舍五入吗?那不是不公平了?再极端一点,20个人,分0.21元呢?
这里我写了很多错的东西,都删了,实践出真知啊。
首先说答案,答案是向下取整而不是四舍五入,看网上标答的代码:
代码:
function getRandomMoney(_redPackage) {
// remainSize 剩余的红包数量
// remainMoney 剩余的钱
//最后一个红包就直接取剩下的钱
if (_redPackage.remainSize == 1) {
_redPackage.remainSize--;
return parseFloat(Math.round(_redPackage.remainMoney * 100) / 100);
}
let r = Math.random();
let min = 0.01; //
let max = _redPackage.remainMoney / _redPackage.remainSize * 2;
//概率乘以max就是应得钱数
let money = r * max;
money = money <= min ? 0.01 : money;
//这里是直接向下取整
money = Math.floor(money * 100) / 100;
_redPackage.remainSize--;
_redPackage.remainMoney -= money;
return money;
}
分析:20个人分0.21元。r从[0~1]中间取,第一个人应该有1/20的概率取到0.02元,这里的max是0.21/20*2
[0~1]加上1/20的概率,这里被变成了,只有0.95及以上才有可能拿到0.02,而
0.95* 0.21/20 *2=0.01995,约等于0.02 想要使 r * max >=0.02 ,r就应该大于0.95238095,与19/20不谋而合。同理,后面几个人是一样的。
我是被困在了1分钱还小的单位里面了,可是这根本没有必要,世界上没有完美的事物,那比0.01还小的单位不应该成为我们思索良久的原因(大不了用精度更大的数据类型)。
最后给出2000次20个人抢0.21元的最后每个人的金额统计
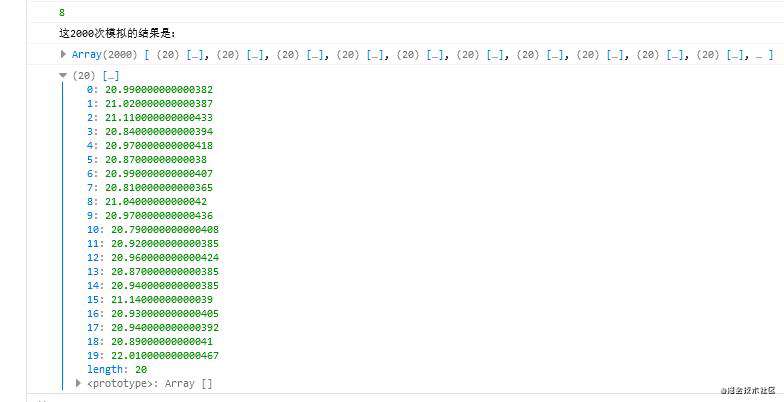
都和21很接近对吧 0.21*2000/20==21 (除了最后一个人,他怎么有22???欧皇?)
不对,我敏锐的察觉到了什么
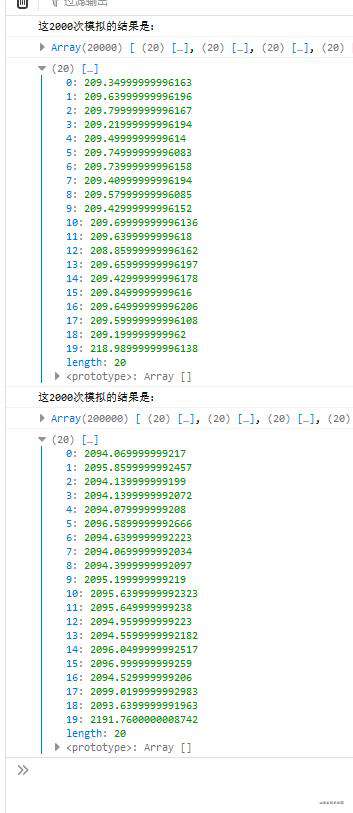
我把2000变成了20000和200000,最后一个人总是高很多
!!!!
我想起了了,因为是向下取整的,所以相当于前19个人都分了一些概率给了最后一个人。。。。
所以,如果你是个连一分钱都不放过的狗贼的话,建议最后一个抢(狗头)(如果你不怕一等,红包就没有的话)
Q1:第一个人只能分到(0,钱数/人数*2),那不是没有分到超大金额的可能了(比如3人分15不能分到14)?
答:别贪啊,你均分就5块钱,(0,10)就是随机区间。再说了,要是第一个人只分到0,第二个人不就是(0,15)随机选了。其实第一个人和第二个人真没什么区别,只要次数够多,最后你从红包里面得的钱都会是公平的平均值(每一次红包里面的钱/每一次红包领取人数)的总和。
Q2:如果我非要实现第一个人也能有概率分到大金额钱应该怎么做?
答:可以啊,比如3人分15,第一个人想从(0,15)里面随机,就得付出更多,他均分应该是5元,就把(0,15)分成(0,5)和(5,15),先概率一次看在(0,5)里面还是在(5,15)里面,在里面再直接随机
设在(0,5)里面的概率是x,那么2.5 x+ 10 *(1-x)= 5 解出来是 x=2/3.
其中2.5是(0,5)的平均值,10是(5,15)的平均值,x是进入(0,5)的概率,区间自然是在0~1之间。
即他有0.666666667的概率进入(0,5)的区间随机取一个数,有0.3333333333的概率进入(5,15)里面随机取一个数作为红包值。
Q3:我可以不向下取整而是四舍五入吗?
绝对不可以,会出现-0.01的情况
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?




发表评论
还没有评论,快来抢沙发吧!