前端玩转位运算(N皇后+Vue3位运算应用)

观感度：?????

口味：东北小炒肉

烹饪时间：10min

初识位运算 记忆

• & ，与 两个位都为 1 时，结果才为 1
• | ，或 两个位都为 0 时，结果才为 0
• ^ ，异或 两个位相同为 0 ，相异为 1
• ～，按位取反 所有 0 变 1，1 变 0
• <<，左移 各二进位全部左移若干位，高位丢弃，低位补 0
• >>，右移 各二进位全部右移若干位，对无符号数，高位补 0 ，有符号数，各编译器处理方法不一样，有的补符号位，有的补 0

理解

其实很简单，小学数学题难度，花几分钟看完如果看懂了请点个赞呗。

左移

二进制左移一位，就是将数字翻倍。

二进制 110101 向左移一位，就是在末尾添加一位 0，也就是 1101010。(此处讨论的是数字没有溢出的情况)

二进制 110101 转化成十进制：

二进制 1101010 转化成十进制：

右移

二进制右移一位，就是将数字除以 2 并求整数商。

二进制 110101 向右移一位，就是去除掉末尾的那一位，也就是 11010 。

二进制 11010 转化成十进制：

无符号右移和有符号右移 （逻辑右移和算术右移）

无符号右移使用 >>> 表示，而有符号右移使用 >> 表示。

>>> 无符号右移 1 位，右边丢弃，左边补 0 即可。

>> 有符号右移保留符号，拷贝最左侧的位来填充左侧，向右位移并丢弃最右边的位。

由于左移位无需考虑高位补 1 还是补 0（符号位可能为 1 或 0），所以不需要区分无符号左移和有符号左移。

位的或

参与操作的位中只要有一个位是 1， 那么最终结果就是 1。

如果我们将 110101 和 100011 进行按位的或操作，就会得到 110111。

位的与

参与操作的位中必须都是 1，最终结果才是 1，否则为 0。

如果我们将 110101 和 100011 进行按位的与操作，就会得到 100001。

位的异或

参与操作的位相同，最终结果是 0 ，否则为 1。

想要得到 1，参与操作的两个位必须不相同，也就是异或中“异”的含义。

如果我们将 110101 和 100011 进行按位的异或操作，就会得到 10110。

常用公式

判断奇偶

x % 2 === 1 -> (x & 1) === 1 (奇数)

x % 2 === 0 -> (x & 1) === 0 (偶数)

x >> 1 -> x / 2

即：x = x / 2; -> x = x >> 1;

mid = (left + right) / 2; -> mid = (left + right) >> 1;

x = x & (x - 1)

清零最低位的 1，代表将最后一位 1 变成 0。

x & -x

得到最低位的 1，代表除最后一位 1 保留，其他位全部为 0。

将 x 最右边的 n 位清零

x & (~0 << n)

获取 x 的第 n 位值

(x >> n) & 1

获取 x 的第 n 位的幂值

x & (1 << (n - 1))

仅将第 n 位置为 1

x | (1 << n)

仅将第 n 位置为 0

x & (~(1 << n))

将 x 最高位至第 n 位(含)清零

x & ((1 << n) - 1)

将第 n 位至第 0 位(含)清零

x & (~((1 << (n + 1)) - 1))

Leecode真题解析 N皇后II

• 原题链接

                    (图片来源LeeCode，同上原题链接)

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

提示：

• 皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一或 N-1 步，可进可退。（引用自 百度百科 - 皇后 ）

理解

皇后可以横、直、斜走，格数不限。题目要求皇后彼此之间不能相互攻击，也就是说需要满足任意两个皇后不能在同一行、同一列以及同一条斜线上。

熟悉这道题的同学，可以看出最直观的做法是利用回溯法进行求解。

遍历枚举出所有可能的选择，依次在每一行放置一个皇后，每次新放置的皇后不能和已经放置的皇后之间存在攻击。

为了降低时间复杂度，最理想的情况是在 O(1) 的时间内判断该位置所在的几条线上是否已经有皇后，可以利用集合来进行位置判断。

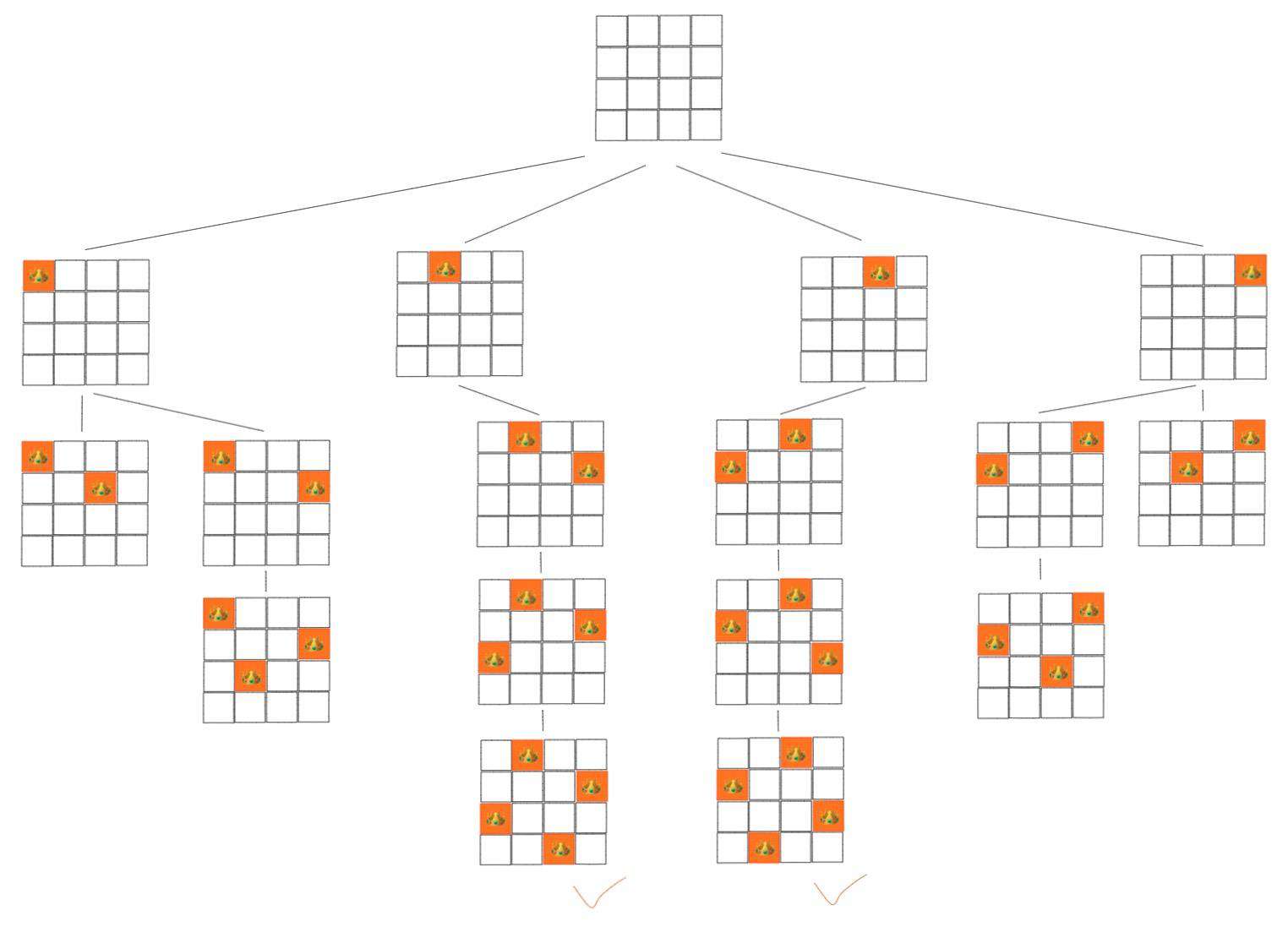
为了让你更好的理解，我利用回溯法将 4 皇后可能的解法画了出来。如下图所示：

一句话理解四种算法思想

• 分治：分而治之，先解决子问题，再将子问题的解合并求出原问题。
• 贪心：一条路走到黑，选择当下局部最优的路线，没有后悔药。
• 回溯：一条路走到黑，手握后悔药，可以无数次重来。(英雄联盟艾克大招无冷却)。
• 动态规划：上帝视角，手握无数平行宇宙的历史存档，同时发展出无数个未来。

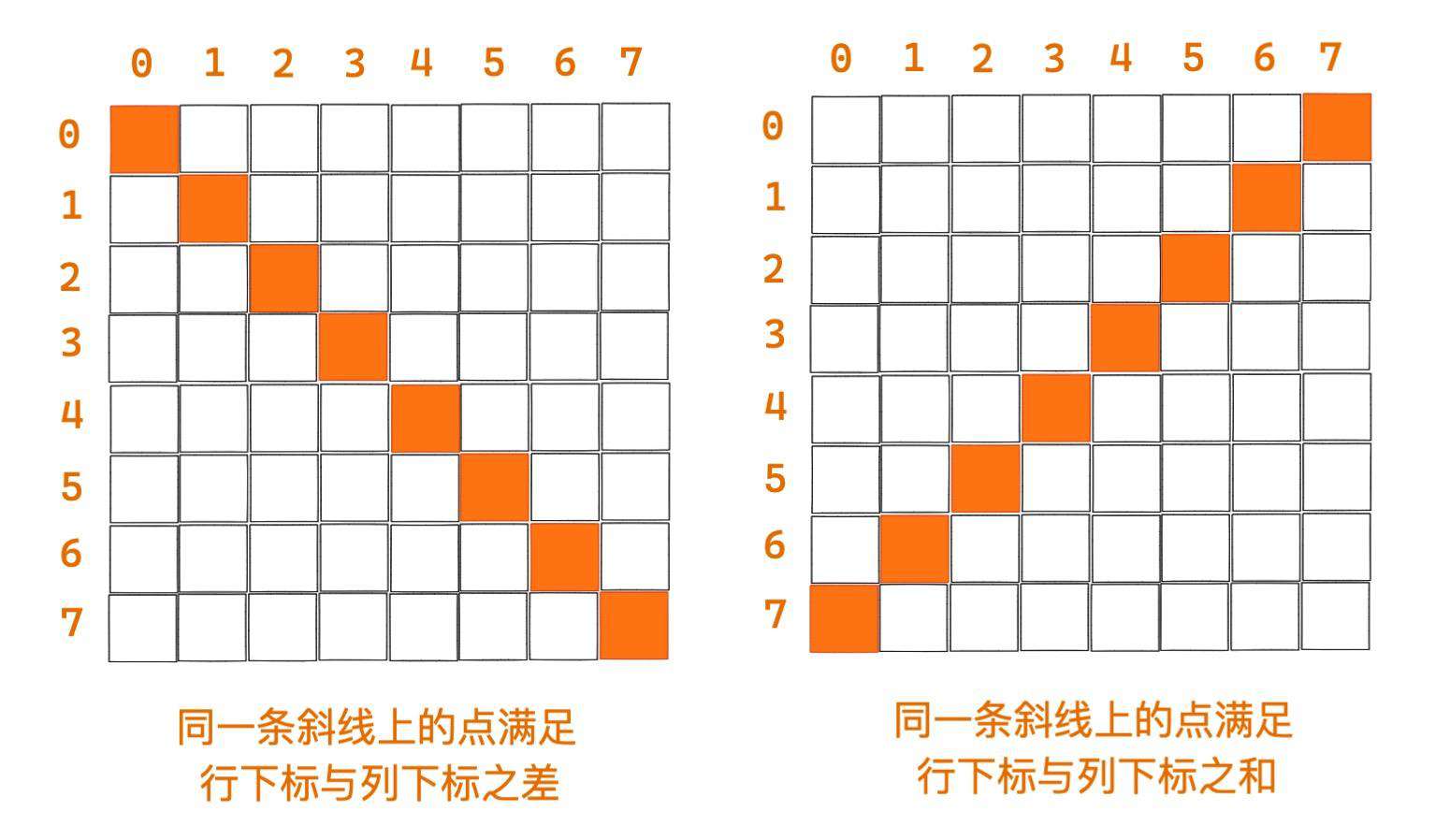
下面这张图是两条对角线方向的斜线的规律，聪明的你肯定一眼就能看出来：

解法一 集合回溯

如下所示是官方给出的题解：

const backtrack = (n, row, columns, diagonals1, diagonals2) => {
    if (row === n) {
        return 1;
    } else {
        let count = 0;
        for (let i = 0; i < n; i++) {
            if (columns.has(i)) {
                continue;
            }
            const diagonal1 = row - i;
            if (diagonals1.has(diagonal1)) {
                continue;
            }
            const diagonal2 = row + i;
            if (diagonals2.has(diagonal2)) {
                continue;
            }
            columns.add(i);
            diagonals1.add(diagonal1);
            diagonals2.add(diagonal2);
            count += backtrack(n, row + 1, columns, diagonals1, diagonals2);
            columns.delete(i);
            diagonals1.delete(diagonal1);
            diagonals2.delete(diagonal2);
        }
        return count;
    }
}
const totalNQueens = function(n) {
    const columns = new Set();
    const diagonals1 = new Set();
    const diagonals2 = new Set();
    return backtrack(n, 0, columns, diagonals1, diagonals2);
};

• 时间复杂度：O(N!)
• 空间复杂度：O(N)

解法二 位运算回溯

学会了位运算，你可以将代码写的更加优雅。

先来明确几个概念和需要用到的公式：

• n：n层
• row：当前层
• cols：列
• pie：撇，左斜线(副对角线)
• na：捺，右斜线(正对角线)
• 二进制为 1，代表不可放置，0 相反
• x & -x ：得到最低位的1 (代表除最后一位 1 保留，其他位全部为 0)
• x & (x - 1)：清零最低位的 1 (代表将最后一位 1 变成 0)
• x & ((1 << n) - 1)：将 x 的最高位至第 n 位(含)清零

思路

将 N 个位置对应成 N 个二进制位，0 代表可以选择，1 代表不能选择。比如八皇后当前第一行的第二位被选择时的状态是 00100000，那么下一行的第二位也不能被选择，正对角线(na)对应的第三位不能被选择(对应当前行右移了一位)，状态表示为：00100000。副对角线(pie)对应的第一位不能被选择(对应当前行左移了一位)，状态表示为 10000000。

const totalNQueens = function(n) {
    let res = 0;
    const dfs = (n, row, cols, pie, na) => {
        if (row >= n) {
            res++;
            return;
        }
        let bits = (~(cols | pie | na)) & ((1 << n) - 1) // 1
        while (bits) { // 2
            let p = bits & -bits // 3
            dfs(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1) // 4
            bits = bits & (bits - 1) // 5
        }
    }
    dfs(n, 0, 0, 0, 0);
    return res;
};

• 时间复杂度：O(N!)
• 空间复杂度：O(N)

代码解读

1.cols ｜ pie ｜ na 表示所有能够被皇后攻击的格子，~(cols | pie | na)取反表示将没有被占的格子从 0 变为 1，以便后续的位遍历。这里用到公式：x & ((1 << n) - 1)：将 x 的最高位至第 n 位(含)清零。一个 int 的二进制位至少有 32 位，我们将前面不需要的位置清零。所以，这行代码表示得到当前所有的空位，也就是可以放置皇后的格子。

2.只要 bits 中有 1，就说明还有格子可以放置皇后，每次遍历都会将其清零(表示在p位置放入了皇后)，也就是注释 5 的代码含义。对应公式：x & (x - 1)：清零最低位的 1 (代表将最后一位 1 变成 0)。

3.对应公式：x & -x ：得到最低位的1 (代表除最后一位 1 保留，其他位全部为 0)，表示当前皇后可放入的位置。

4.修改状态，进入下一层递归。row + 1 代表搜索下一行，cols ｜ p 代表目前所有可以放置皇后的列。(pie | p) << 1 ，(na | p) >> 1，在上面思路中已经说过了，不再赘述。

Vue3 中的位运算之 shapeFlags、patchFlags

Vue3 中也有一些关于位运算的实践。

shapeFlags

shapeFlags 针对 VNode 的 type 进行了更详细的分类，便于在 patch 阶段，根据不同的类型执行相应的逻辑。

可以点击此处跳转到源码仓库进行查看

// packages/shared/src/shapeFlags.ts
export const enum ShapeFlags {
  ELEMENT = 1, // HTML 或 SVG 标签 普通 DOM 元素
  FUNCTIONAL_COMPONENT = 1 << 1, // 函数式组件
  STATEFUL_COMPONENT = 1 << 2, // 普通有状态组件
  TEXT_CHILDREN = 1 << 3, // 子节点是纯文本
  ARRAY_CHILDREN = 1 << 4, // 子节点是数组
  SLOTS_CHILDREN = 1 << 5, // 子节点是插槽
  TELEPORT = 1 << 6, // Teleport
  SUSPENSE = 1 << 7, // Suspense
  COMPONENT_SHOULD_KEEP_ALIVE = 1 << 8, // 需要被 keep-alive 的有状态组件
  COMPONENT_KEPT_ALIVE = 1 << 9, // 已经被 keep-alive 的有状态组件
  COMPONENT = ShapeFlags.STATEFUL_COMPONENT | ShapeFlags.FUNCTIONAL_COMPONENT // 有状态组件和函数组件都是组件，用 COMPONENT 表示
}

patchFlags

patchFlags 用于标识节点更新的类型，用于运行时优化。

// packages/shared/src/patchFlags.ts
export const enum PatchFlags {
  TEXT = 1, // 动态文本节点
  CLASS = 1 << 1, // 动态 class
  STYLE = 1 << 2, // 动态 style
  PROPS = 1 << 3, // 动态属性
  FULL_PROPS = 1 << 4, // 具有动态 key 属性，当 key 改变时，需要进行完整的 diff 比较
  HYDRATE_EVENTS = 1 << 5, // 具有监听事件的节点
  STABLE_FRAGMENT = 1 << 6, // 子节点顺序不会被改变的 fragment
  KEYED_FRAGMENT = 1 << 7, // 带有 key 属或部分子节点有 key 的 fragment
  UNKEYED_FRAGMENT = 1 << 8, // 子节点没有 key 的 fragment
  NEED_PATCH = 1 << 9, // 非 props 的比较，比如 ref 或指令
  DYNAMIC_SLOTS = 1 << 10, // 动态插槽
  DEV_ROOT_FRAGMENT = 1 << 11, // 仅供开发时使用，表示将注释放在模板根级别的片段
  HOISTED = -1, // 静态节点
  BAIL = -2 // diff 算法要退出优化模式
}

通过进行 ｜ 或运算进行标记的组合，如果当前节点是一个动态文本节点(0000 0001)，它同时又具有动态 style (0000 0100)，二者进行 ｜ 或运算后值为 (0000 0101)。

通过进行 & 与运算进行标记的检查。可以点击此处跳转到源码仓库进行查看

读这部分注释的时候发现了引用文件路径的错误，提交了Pr，成功混入了 Vue Contributor，与尤大进行了一波亲密互动。

所以说，好好学习是有回报的，一起加油吧，打工人！

如果你对 Vue3 DOM Diff 核心算法感兴趣的话，也欢迎阅读我的另外一篇专栏，Vue3 DOM Diff 核心算法解析

更有其他算法系列专栏，让你一次看过瘾：

• 前端如何搞定数据结构与算法(先导篇)
• 「时间管理」JavaScript算法时间、空间复杂度分析
• 你真的懂递归吗？
• 分治、动态规划、回溯、贪心一锅炖
• 「种树专业户」“树”业有专攻
• 从酒桌游戏看二分查找算法
• 面试链表不再怕
• 食堂店小二儿教你学会栈

❤️爱心三连击

1.如果你觉得食堂酒菜还合胃口，就点个赞支持下吧，你的赞是我最大的动力。

2.关注公众号前端食堂，吃好每一顿饭！

3.点赞、评论、转发 === 催更！