这是我参与8月更文挑战的第23天，活动详情查看：8月更文挑战
啥是三门问题
三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论。最初来源于漂亮国的一个游戏类的电视节目。节目名字叫做《Let's make a deal》.
从名字上大概能看出，节目就是出一些选择性质的题目，让参与者做决定。
下面是一道题目的内容：
“假设你正在参加一个游戏节目，你被要求在三扇门中自由选择一扇门：其中一扇后面有一辆车；其余两扇后面则是山羊。你将得到的奖品是你选择的门的后面的物品（山羊或者汽车）。
你随机选择了一扇门，假设是一号门，然后知道门后面有什么的主持人，开启了另一扇后面有山羊的门，假设是三号门。他然后问你：“你想改变之前的选择，重新选择二号门吗？”
在这个题目中，选中门后有汽车的门奖品就是汽车，否则奖品就是山羊，大部分参与者都希望自己的奖品是汽车。
那么在主持人问你之后，你会改变自己最开始选择的门吗？会从一号门选择二号门吗？
你也许会疑问，这有什么好纠结的，换不换不是一样的吗？
其实这个问题本质是：换另一扇门是否会增加参赛者赢得汽车的概率？
如果严格按照上述题目的条件，即主持人清楚地帮你打开了一扇背后是山羊的门，那么答案是：会。
不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。
看到了这里，对于你或者我或者大部分人而言，都觉得这个答案十分的出乎意料。因为日常的生活赋予我们的直觉会让我们觉得，换或者不换，赢得汽车的概率都是三分之一才对。
这就是有趣的地方，虽然这个问题的答案在逻辑上并不自相矛盾，但十分的违反直觉。所以这个问题曾引起一阵广泛而热烈的讨论。
逻辑上的解释
逻辑学上有很多种解释的方案，我这里只列举两种逻辑学解释。
第一种解释
现在给你两种方案：
第一种，你选择一扇门，然后坚定不移的打开它，如果它有汽车，那么你中奖了
第二种，你选择一扇门，然后排除此门打开另外两道门，如果打开的两道门中有汽车，那么你中奖了。
聪明如你，肯定体会到了这两种方案的差异。 其实不换门，就是第一种方案，而换门，就等同于你采用了第二种方案。
第二种解释
换门本质上采用了排除法。在你还没有作出选择的时候：
- 选中山羊的概率是三分之二
- 选中汽车的概率是三分之一。
所以第一次你的随机选择，大概率选到了山羊（因为是三分之二的概率），然后主持人又帮你排除了另一扇有山羊的门。
这个过程就相当于你连续选择了两次：
- 你有三分之二的概率选择了一道有山羊的门
- 主持人帮你选择了另一道山羊的门
此时用排除法，将这两扇门排除-（1- 2/3 - 1）= 2/3
那么剩下的那一扇门有汽车的概率是三分之二。
画图来说明
我知道很多人还是不服气的，即便上面逻辑上的解释，也不是那么容易让人信服。
所以我画了一张图来说明答案。
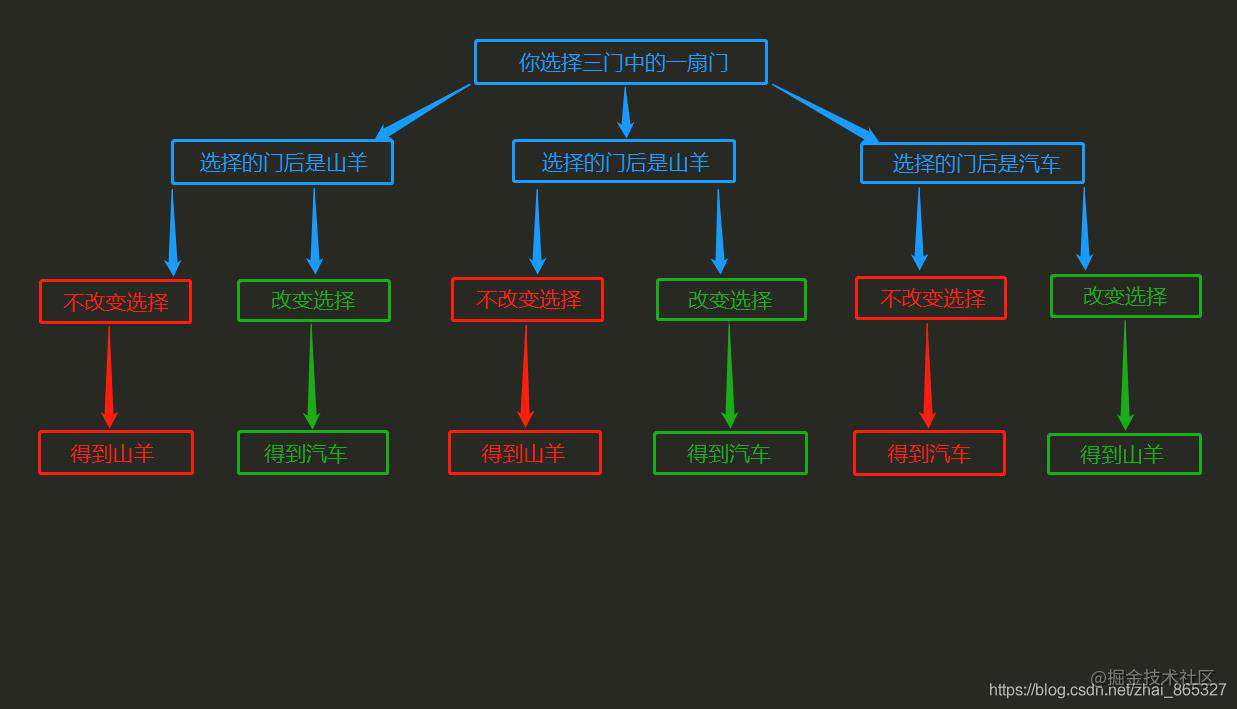从图中显而易见的看出，当你改变选择时，有三分之二的机会得到汽车，否则，有三分之二的机会得到山羊。
通过程序来验证
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, user-scalable=no, initial-scale=1.0, maximum-scale=1.0, minimum-scale=1.0" />
<meta name="apple-mobile-web-app-capable" content="yes" />
<meta name="apple-mobile-web-app-status-bar-style" content="black" />
<meta name="x5-orientation" content="landscape" />
<meta name="x5-fullscreen" content="true" />
<meta name="screen-orientation" content="landscape" />
<meta name="full-screen" content="true" />
<meta name="viewport" content="uc-fitscreen=yes" />
<meta name="nightmode" content="disable" />
<title>三门问题验证</title>
<style>
html,
body {
font-size: 100px;
height: 100%;
}
#app {
height: 6rem;
font-size: 0.4rem;
text-align: center;
display: flex;
}
button {
font-size: 1rem;
background-color: #0f0;
margin: auto;
border-radius: 8px;
}
</style>
</head>
<body>
<div style="text-align:center">验证三门问题</div>
<div id="app">
<button onclick="init()">click ME !!!</button>
</div>
</body>
<script>
var n = 10000,
win = 0,
lose = 0,
doors = null,
chooseIndex = NaN,
leftDoor = NaN;
function random(ind) {
return Math.floor(Math.random() * ind)
}
function randerDoors() { // 随机在一个门后放置汽车
doors = (new Array(3)).fill(false) // 初始化门后全部是山羊
var ind = random(3)
doors[ind] = true
}
function chooseDoors() { // 参与者随机选择一扇门
chooseIndex = random(2)
}
function openDoors() { // 主持人随机打开一扇门
if (doors[chooseIndex]) { // 如果参与者第一次选中的汽车
const ind = random(2)
leftDoor = (chooseIndex + ind) % 3 // 剩下的那个门的索引
lose++
} else { // 如果参与者第一次选中的山羊
if (doors[(chooseIndex + 1) % 3]) {
leftDoor = (chooseIndex + 1) % 3
} else {
leftDoor = (chooseIndex + 2) % 3
}
win++
}
}
var el = document.getElementById('app')
function init() {
for (var i = 0; i < n; i++) {
randerDoors()
chooseDoors()
openDoors()
}
el.innerHTML = '<p>You have win <strong>' + win + '</strong> cars and <strong>' + lose + '</strong> sheep</p>'
}
</script>
</html>
注释写的很清楚，大家把代码复制到本地，就可以在浏览器打开看结果了。
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用？
- 本站所有资源版权均属于原作者所有，这里所提供资源均只能用于参考学习用，请勿直接商用。若由于商用引起版权纠纷，一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了？
- 找不到素材资源介绍文章里的示例图片？
- 模板不会安装或需要功能定制以及二次开发？
发表评论
还没有评论，快来抢沙发吧！