ShaderJoy ——旋转的分层齿轮【GLSL】

效果图

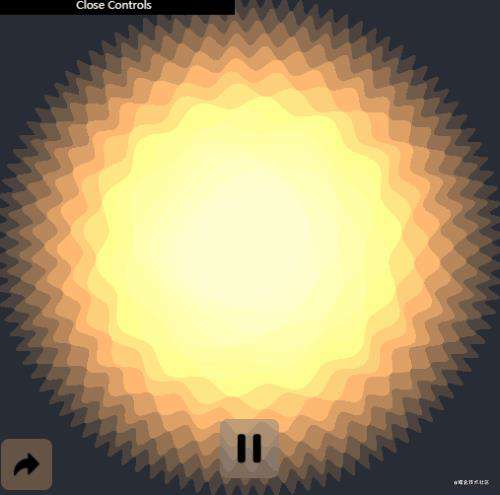
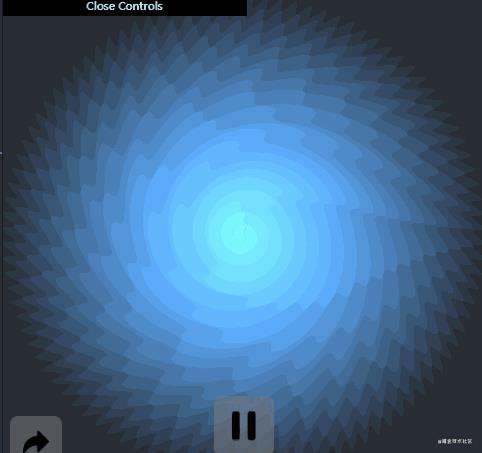
正文

首先，我们将获得一个范围 [-1., 1.] 之间的 uv 坐标，即屏幕中心是 (0., 0.) 点

vec2 uv = (u * 2. - res.xy) / res.xy ;

然后我们据此计算出每个 uv 坐标到中心点的距离（圆的半径）

r = length(uv)

可视化后的效果如下所示【越黑值越小，越白值越大】

ShaderJoy ——旋转的分层齿轮【GLSL】

接下来我们据此来对圆域进行分层，没错就是我们的老朋友 —— floor 函数

float i = floor(r * N); ///< 圆域分层

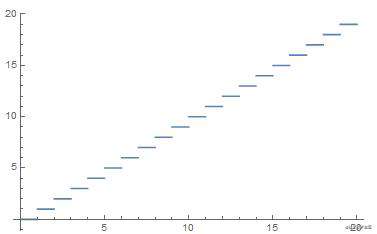
ShaderJoy ——旋转的分层齿轮【GLSL】

其实际函数如下

ShaderJoy ——旋转的分层齿轮【GLSL】

为了让对比度层次更加具有 “艺术性”，可以给它一个指数函数

floor(pow(128., i / N))

其函数图就变成了这样

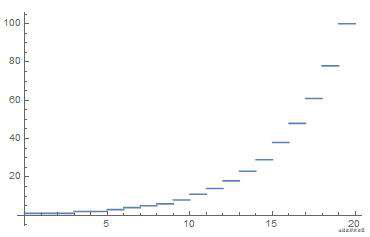
ShaderJoy ——旋转的分层齿轮【GLSL】

可视化后为

ShaderJoy ——旋转的分层齿轮【GLSL】

那么这个对比度分层的圆域有什么用呢？

其实它是作用于像素的角度的

a = atan(uv.y, uv.x);
a *= floor(pow(128., i / N)); ///< 指数分阶

原 atan(uv.y, uv.x) 的函数可视化如下【由于 y 轴是上下相反的，所以函数图和 shader 可视化的效果图也是上下颠倒的】

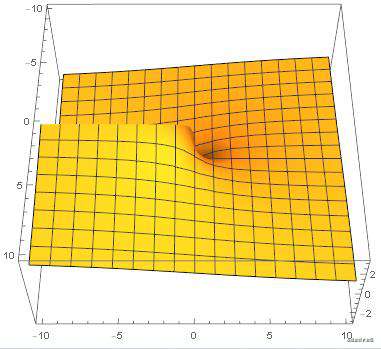
ShaderJoy ——旋转的分层齿轮【GLSL】

shader 实际效果图

ShaderJoy ——旋转的分层齿轮【GLSL】

经过我们之前准备的指数量化的圆域后，其 shader 可视化的效果为

ShaderJoy ——旋转的分层齿轮【GLSL】

其实，此时将像素角度经过 cos 函数，再配合分阶的半径，我们就可以达成以下锯齿的效果

r +=  (.5 + .5 * cos(a)) / N; ///< 齿轮状r = floor(N * r) / N; ///< 齿轮状效果后，半径再分阶

ShaderJoy ——旋转的分层齿轮【GLSL】

通过给它着色来进一步美化，得到如下效果

o = (1. - r) * vec4(3, 2, 1, 1);

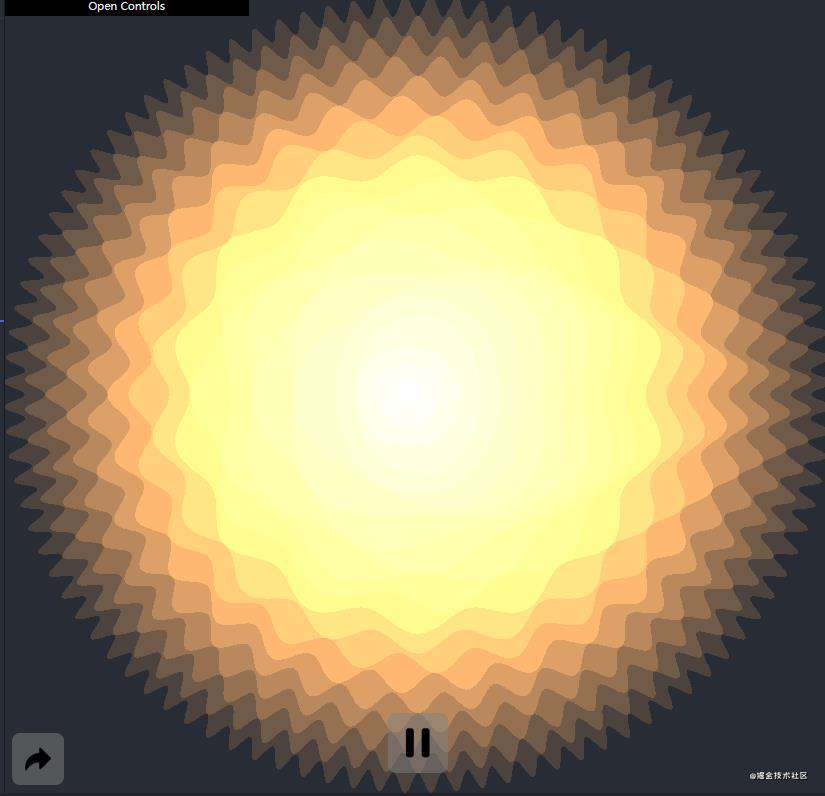
ShaderJoy ——旋转的分层齿轮【GLSL】

最后一步，因为静止的 “齿轮” 还是略显单调，我们可以通过让像素的角度随着时间变化，让 “齿轮” 运动起来

a += 10.*t +     ///< 旋转     123.34 * i; ///< 各层的角度差别

其效果为

ShaderJoy ——旋转的分层齿轮【GLSL】

稍加修改（两处代码），我们还可以得到如下效果

第一处，像素角度随着时间变化的代码

a += 20.*sin(.5 * t) + 123.34 * i - 100.*r * cos(.5 * t); // (r-0.*i/N)

第二处，着色代码

 o = (1. - r) * vec4(.5, 1, 1.5, 1);

ShaderJoy ——旋转的分层齿轮【GLSL】

完整的代码

#define N 20.#define res iResolutionvoid mainImage( out vec4 o, vec2 u ){    vec2 uv = (u * 2. - res.xy) / res.xy ;    float t = iTime,          r = length(uv),          a = atan(uv.y, uv.x);    float i = floor(r * N); ///< 圆环分层    a *= floor(pow(128., i / N)); ///< 指数分阶#ifdef EFFECT_0    a += 10.*t +     ///< 旋转             123.34 * i; ///< 角度分阶#else    a += 20.*sin(.5 * t) + 123.34 * i - 100.*r * cos(.5 * t); // (r-0.*i/N)#endif    r +=  (.5 + .5 * cos(a)) / N; ///< 齿轮状    r = floor(N * r) / N;         ///< 齿轮状效果后，半径再分阶#ifdef EFFECT_0    o = (1. - r) * vec4(3, 2, 1, 1); ///< 反向着色#else        o = (1. - r) * vec4(.5, 1, 1.5, 1);#endif}

常见问题FAQ

免费下载或者VIP会员专享资源能否直接商用？: 本站所有资源版权均属于原作者所有，这里所提供资源均只能用于参考学习用，请勿直接商用。若由于商用引起版权纠纷，一切责任均由使用者承担。更多说明请参考 VIP介绍。

提示下载完但解压或打开不了？: 最常见的情况是下载不完整: 可对比下载完压缩包的与网盘上的容量，若小于网盘提示的容量则是这个原因。这是浏览器下载的bug，建议用百度网盘软件或迅雷下载。若排除这种情况，可在对应资源底部留言，或联络我们.。

找不到素材资源介绍文章里的示例图片？: 对于PPT，KEY，Mockups，APP，网页模版等类型的素材，文章内用于介绍的图片通常并不包含在对应可供下载素材包内。这些相关商业图片需另外购买，且本站不负责(也没有办法)找到出处。同样地一些字体文件也是这种情况，但部分素材会在素材包内有一份字体下载链接清单。