树结构的经典问题之自平衡树
BST树存在一个问题:取决于你添加的节点数,树的一条边可能会非常深;也就是说,树的一条分支会有很多层,而其他的分支却只有几层,如下图所示
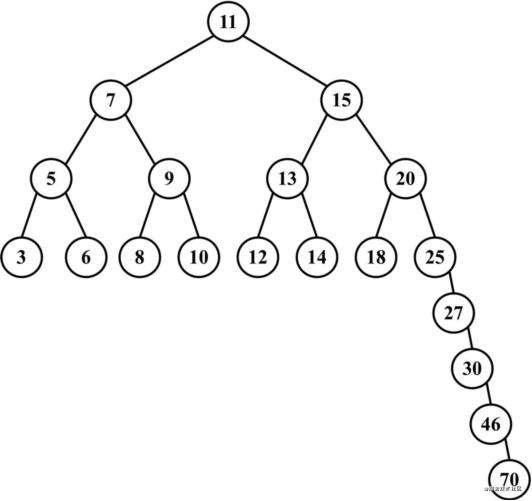
这样,在需要在某条边上添加、移除和搜索某个节点的时候,会引起一些性能问题。
为了解决这个问题,有一种树叫作Adelson-Velskii-Landi 树(AVL 树)。
AVL树是一种自平衡二叉搜索树,意思是任何一个节点左右两侧子树的高度之差最多为1。
理清基本概念
节点的高度
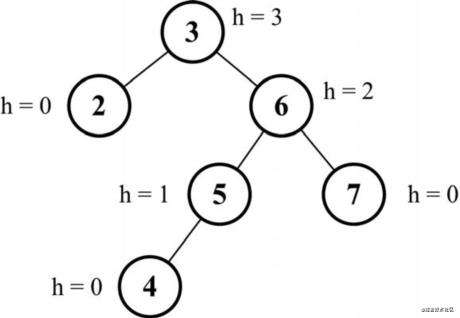
如上图所示:
根节点3的左侧除了一个子节点2再也没有其他子节点,而节点2本身也是叶节点,所以左侧子树的高度就为0;
根节点3的右侧有一个子节点6,子节点6下方左右两侧都有子节点,其左侧子节点5下方还有一个叶节点4,所以节点4的高度是0,节点5的高度是1;
节点6的右侧有一个子节点7,而节点7下面也没有其他子节点,所以节点7也是叶节点,所以节点7的高度也是0;
节点6作为节点5和节点7的父节点,它的高度要以左右两侧中最高的一方为准,所以节点6的高度要在节点5的高度1之上再加1,即节点6的高度为2;
而根节点3又作为节点2和节点6的父节点,节点3的高度也要以左右两侧中最高的一方为准,所以根节点3的高度要在节点6的高度2之上再加1,即根节点3的高度为3。
平衡因子
在AVL树中,需要对每个节点计算右子树高度(hr)和左子树高度(hl)之间的差值,该值(hr-hl)应为0、1或-1,如下图所示:
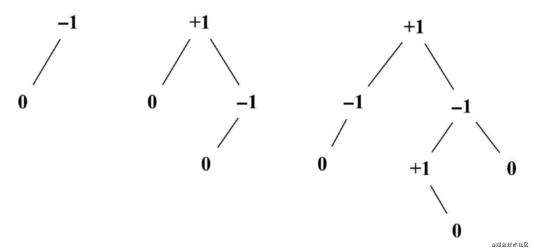
如果结果不是这三个值之一,则需要平衡该AVL树。这就是平衡因子的概念。
平衡操作
在对AVL树添加或移除节点后,要计算并验证树是否需要进行平衡。向AVL树插入节点时,可以执行单旋转或者双旋转两中平衡操作,分别对应四种场景:
场景一:
左左(LL):向右的单旋转
此时又可细分为两种情况:
情况1:
节点的左侧子节点的右下方没有子节点且左侧偏重,如下图所示:
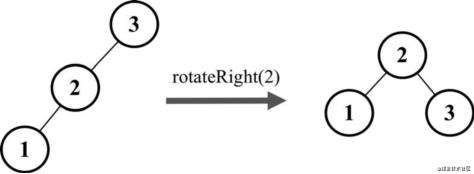
根节点3的左侧子节点2的左侧有子节点1,节点2的右侧没有子节点,此时只需要将节点2作为新的根节点,节点3变成新的根节点2的右侧子节点即可保持平衡
情况2:
节点的左侧子节点的左侧偏重,且左侧子节点的右侧有子节点,如下图所示:
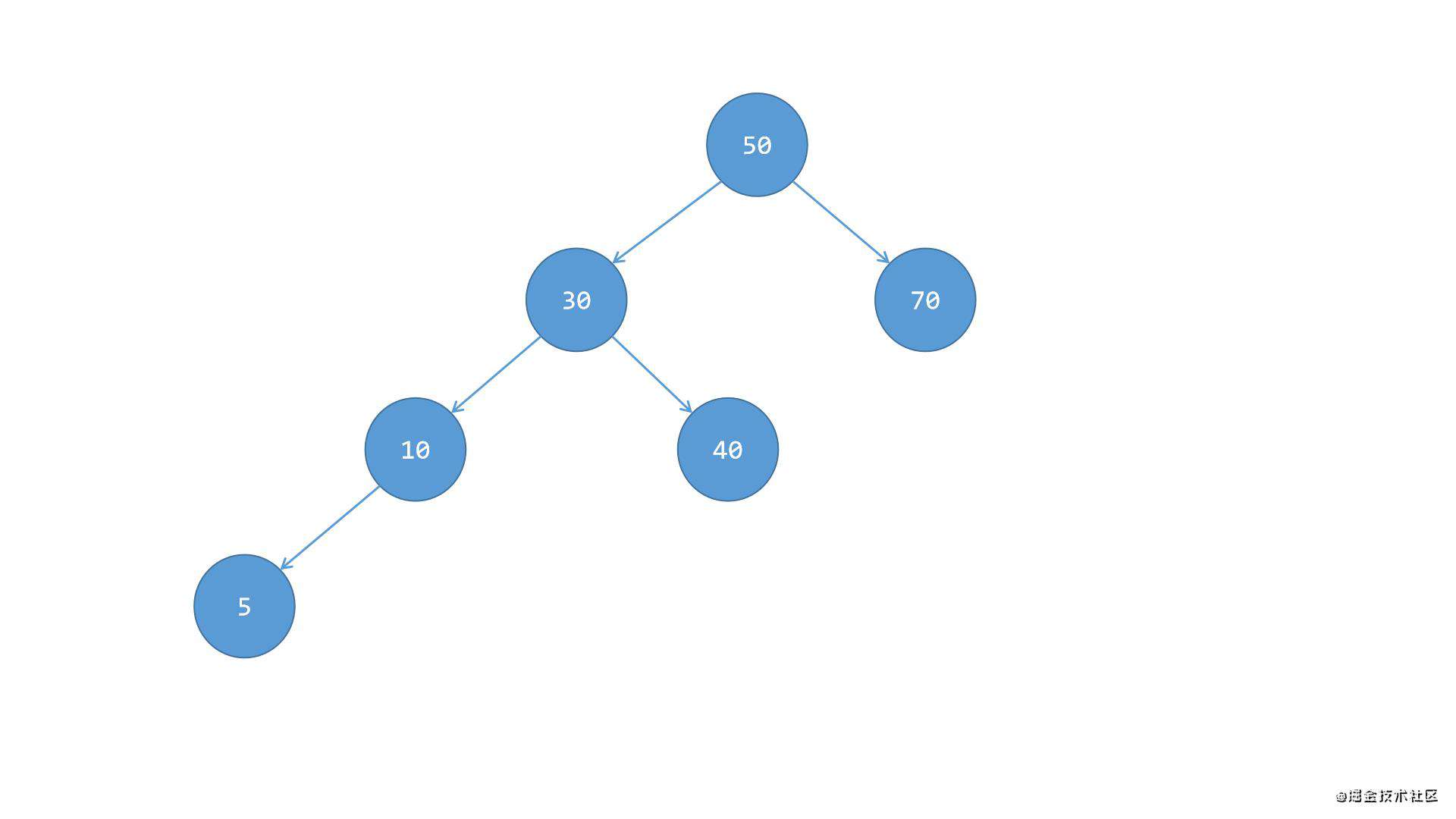
根节点50的左侧子树30偏重,且左侧子树30的左侧子节点10的左下方也有子节点5,而左侧子树30的右侧子节点40没有子节点,自己就是叶节点。此时需要平衡的话:
第一步,先将左侧子树30与根节点50分离,如下图所示:
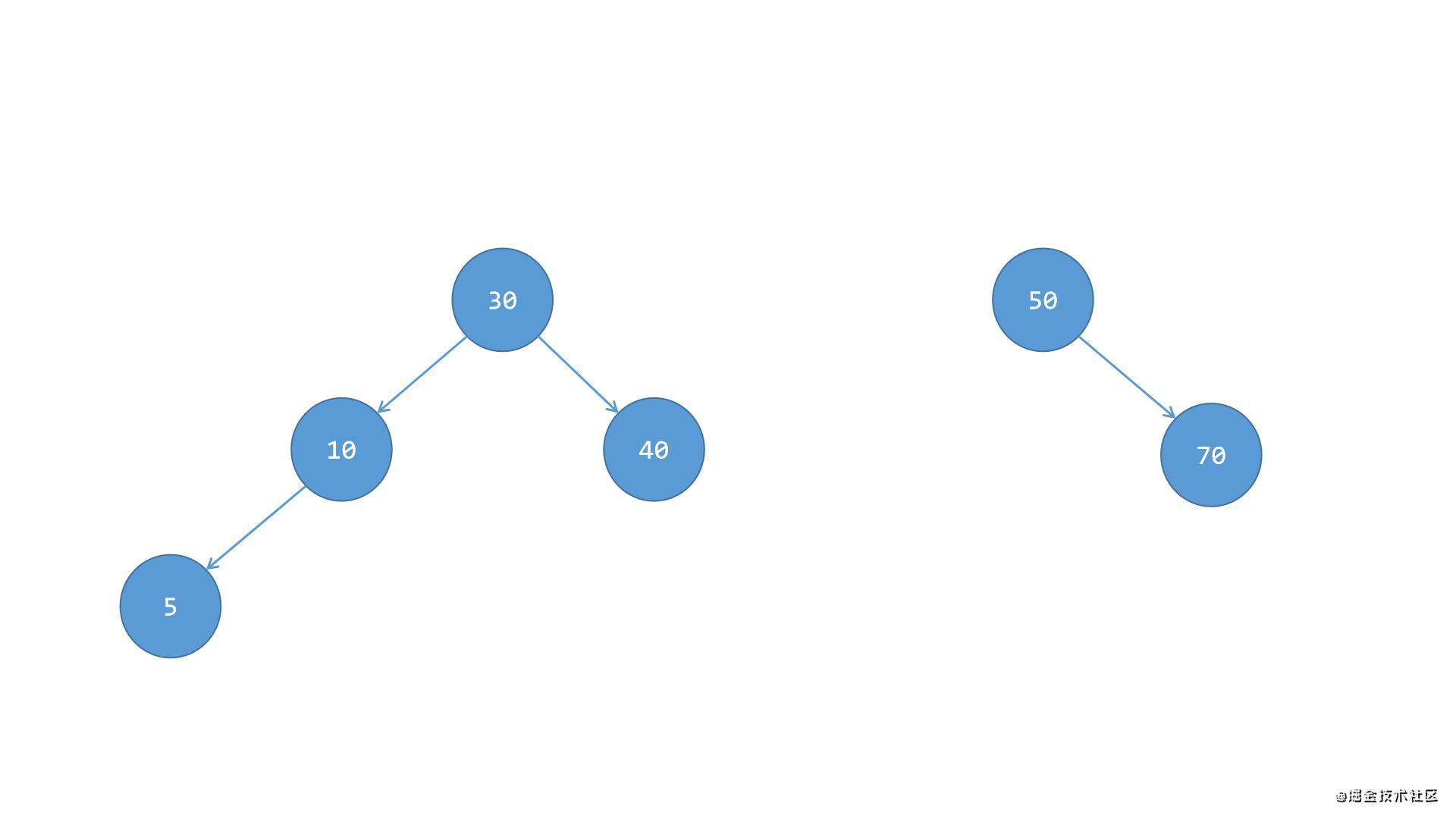
第二步,将节点30下方的右侧子节点40抽离出来,移植到节点50的左侧,成为节点50的左侧子节点,如下图所示:
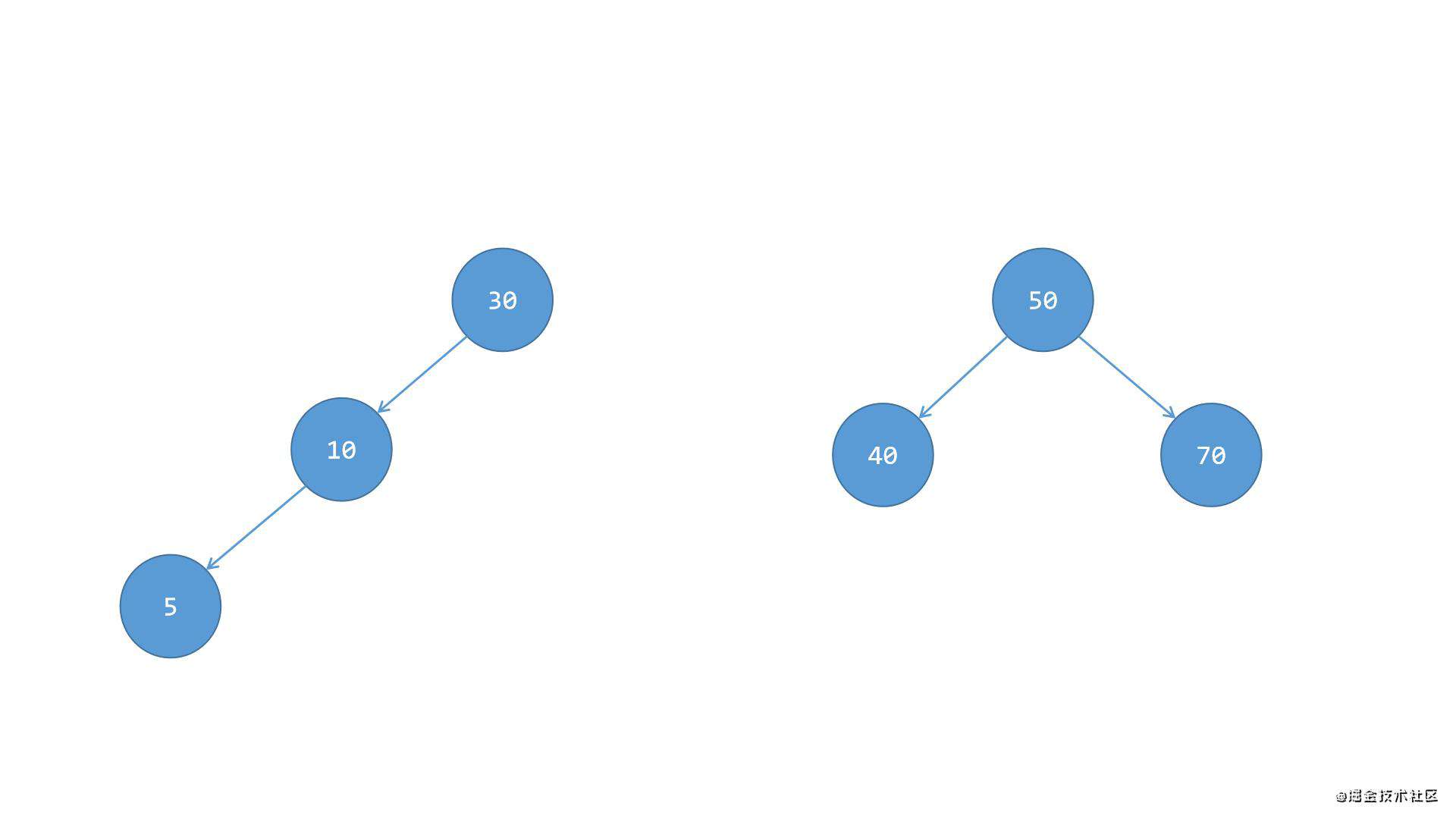
第三步,将节点50这一系,整体移植到节点30右侧,成为节点30的右侧子树,这样就完成了平衡,如下图所示:
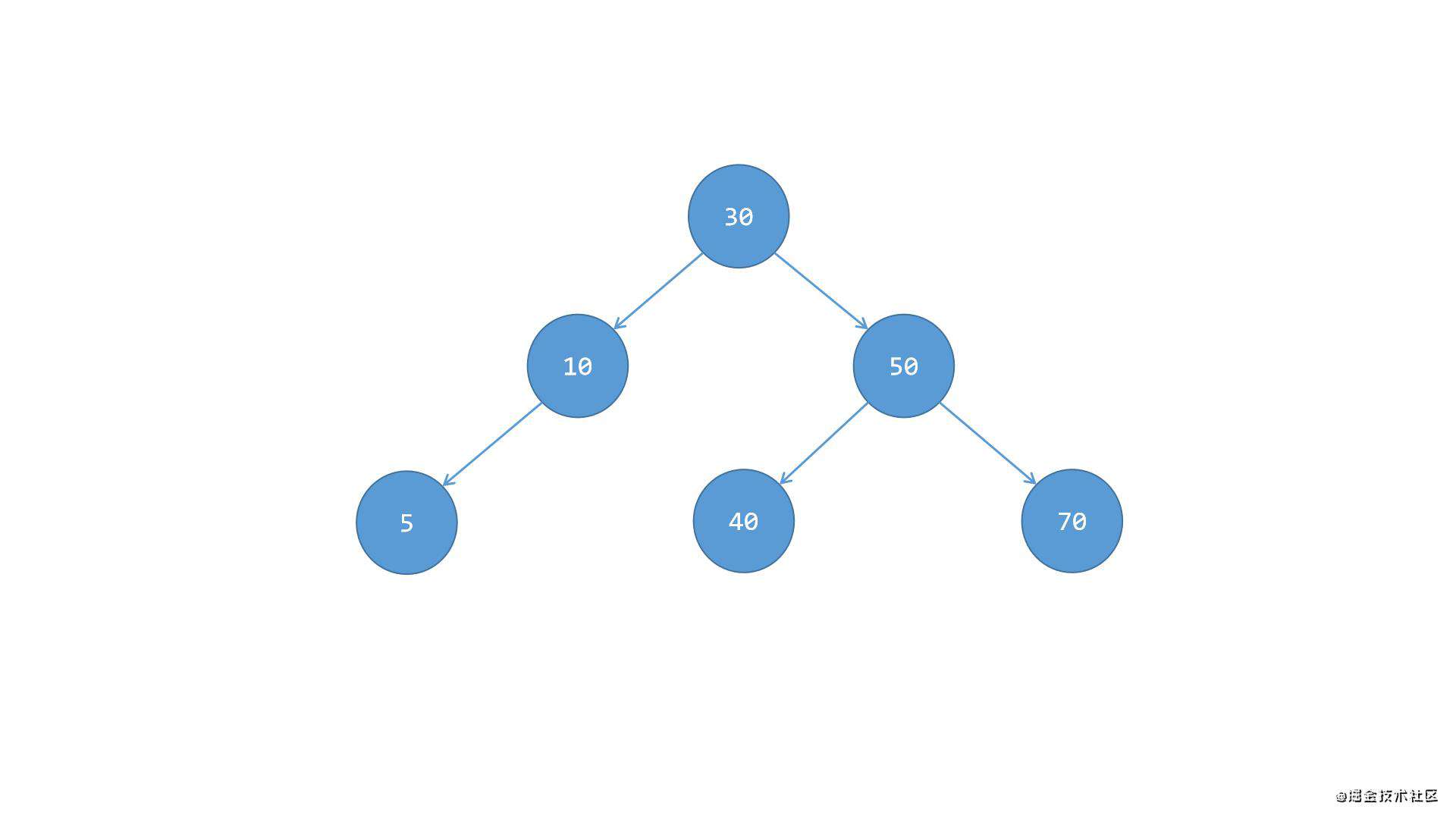
综上所述,LL使用场景为:节点的左侧子节点的高度大于右侧子节点的高度时,并且左侧子节点也是平衡或者左侧较重的情况。
场景二:
右右(RR):向左的单旋转
此时又可细分为两种情况:
情况1:
节点的右侧子节点的左下方没有子节点且右侧偏重,如下图所示:
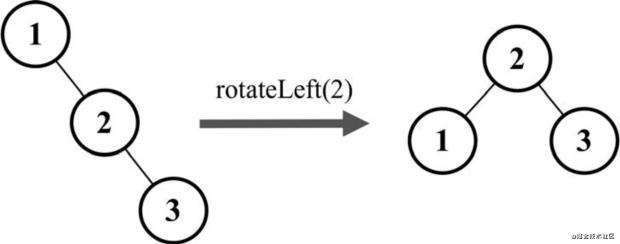
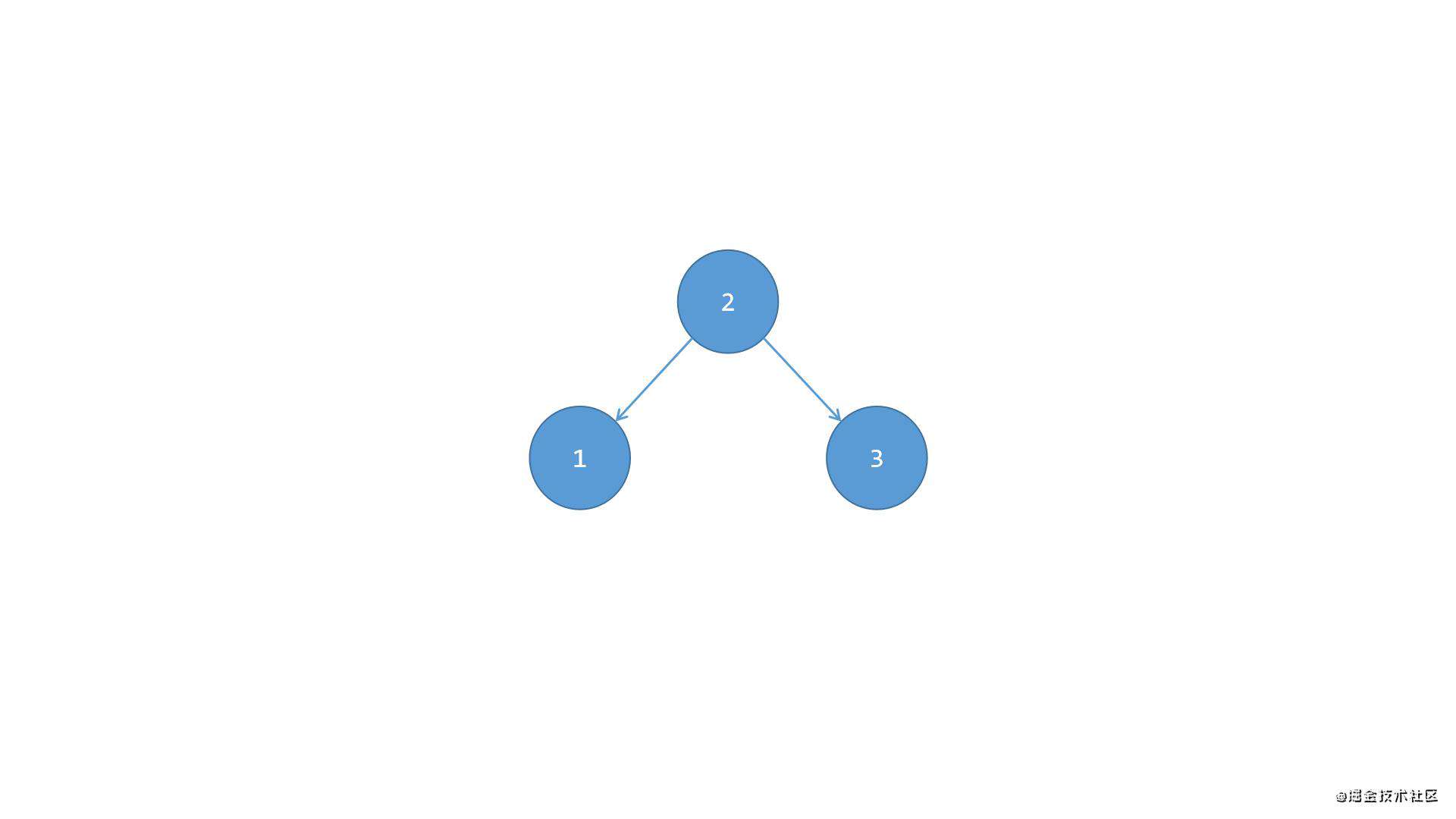
根节点1的右侧子节点2的右侧有子节点3,节点2的左侧没有子节点,此时只需要将节点2作为新的根节点,节点1变成新的根节点2的左侧子节点即可保持平衡
情况2:
节点的右侧子节点的右侧偏重,且右侧子节点的左侧有子节点,如下图所示:
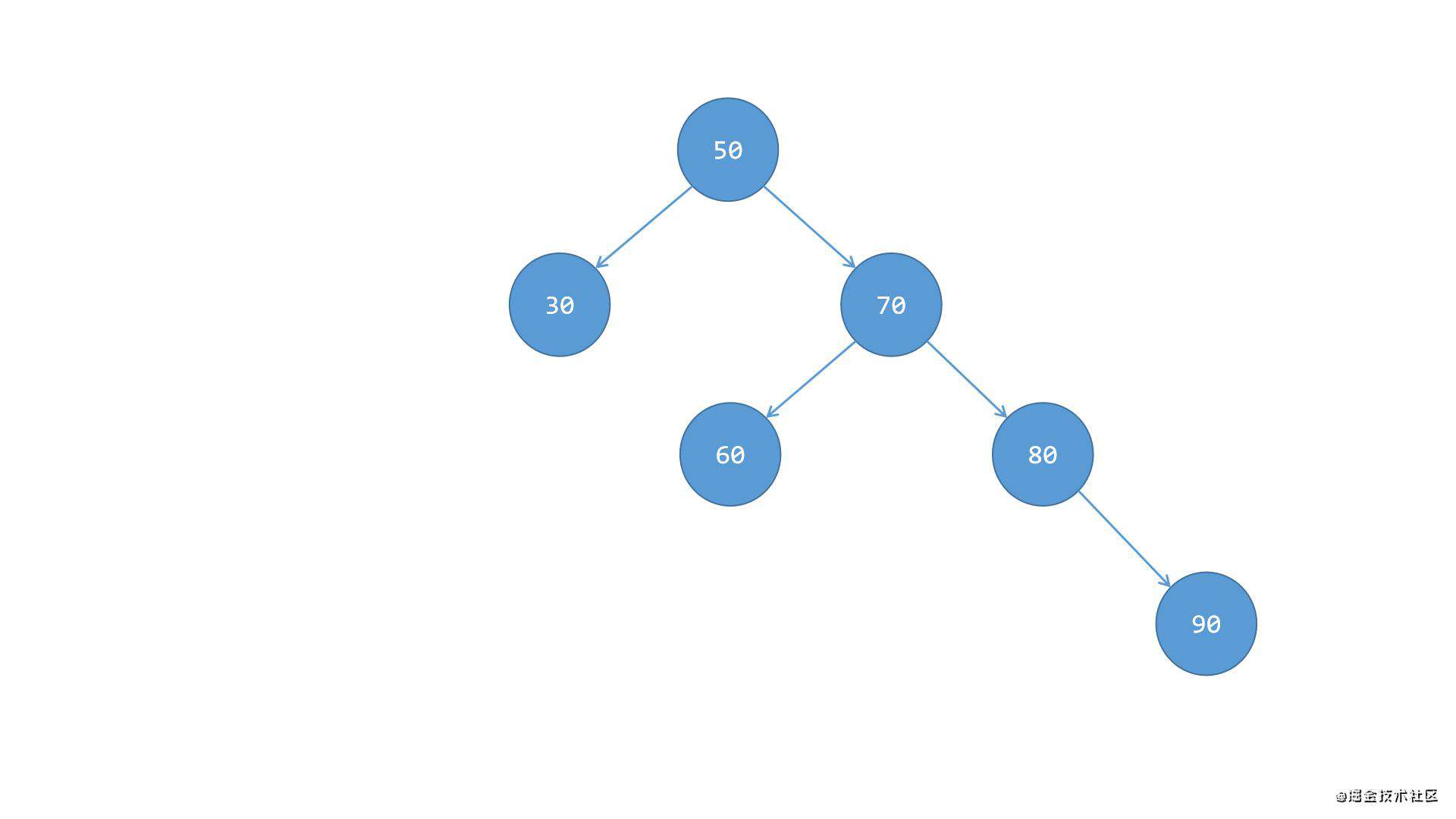
根节点50的右侧子树70偏重,且右侧子树70的右侧子节点80的右下方也有子节点90,而右侧子树70的左侧子节点60没有子节点,自己就是叶节点。此时需要平衡的话:
第一步,先将右侧子树70与根节点50分离,如下图所示:
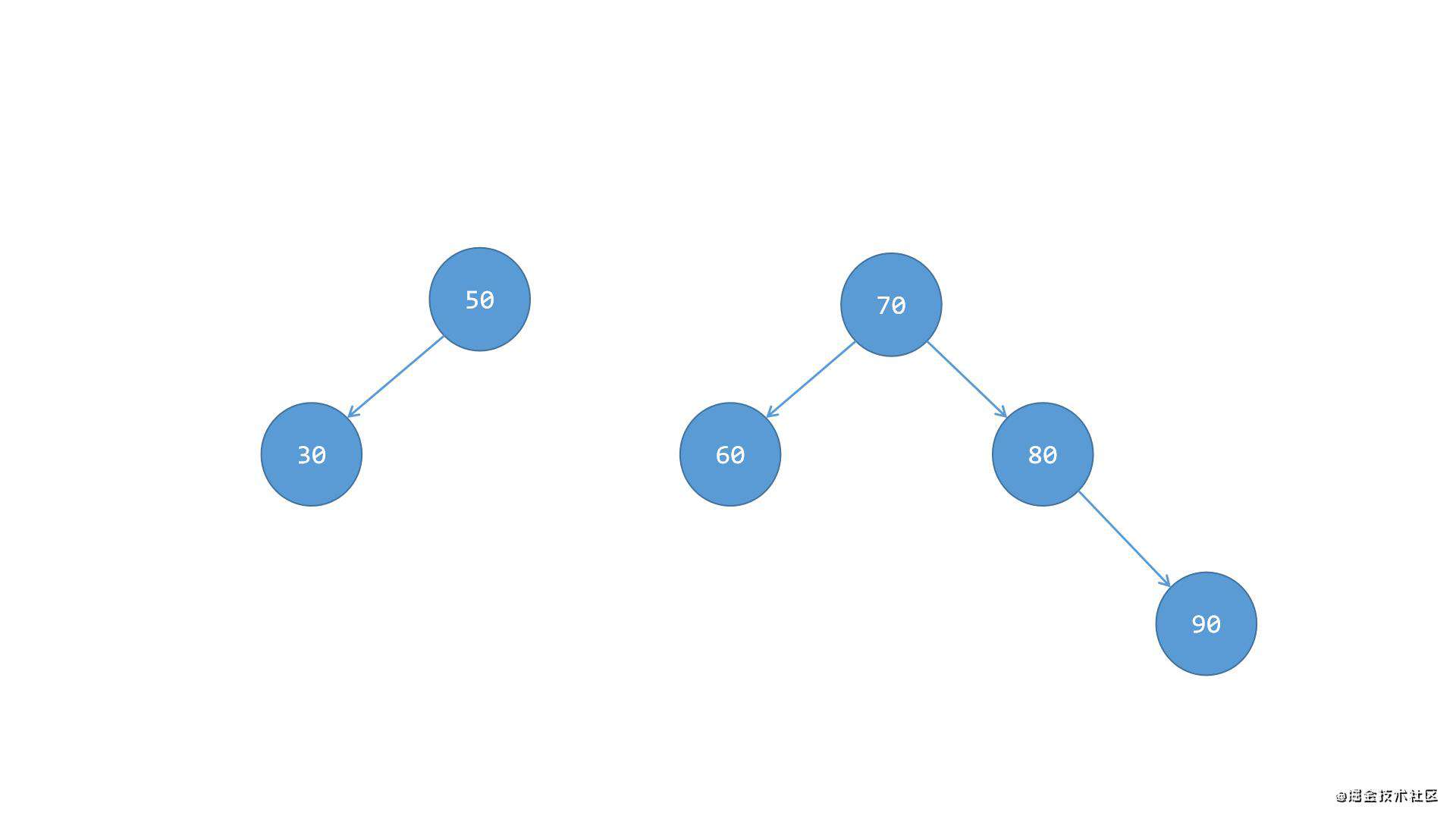
第二步,将节点70下方的左侧子节点60抽离出来,移植到节点50的右侧,成为节点50的右侧子节点,如下图所示:
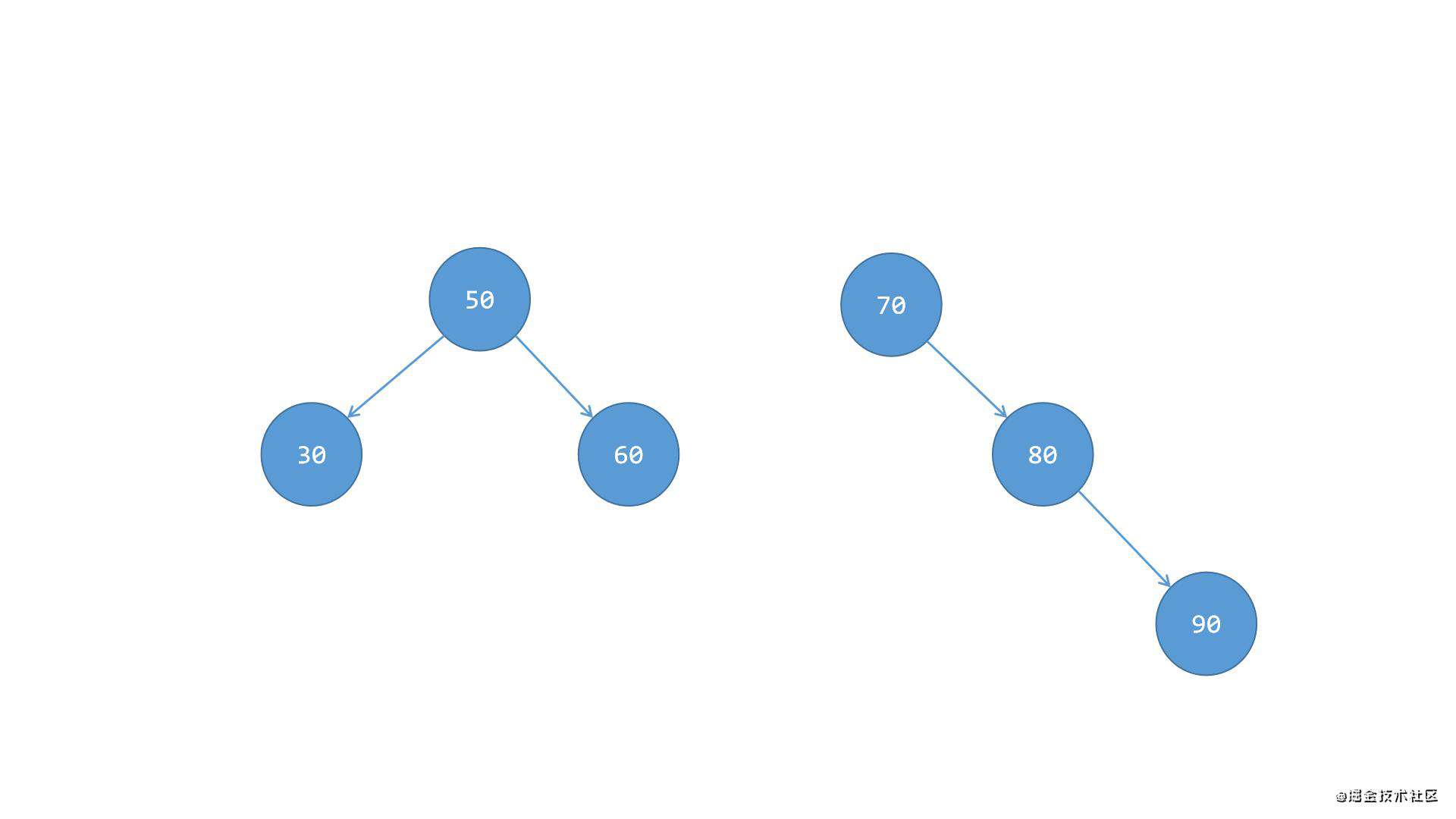
第三步,将节点50这一系,整体移植到节点70左侧,成为节点70的左侧子树,这样就完成了平衡,如下图所示:
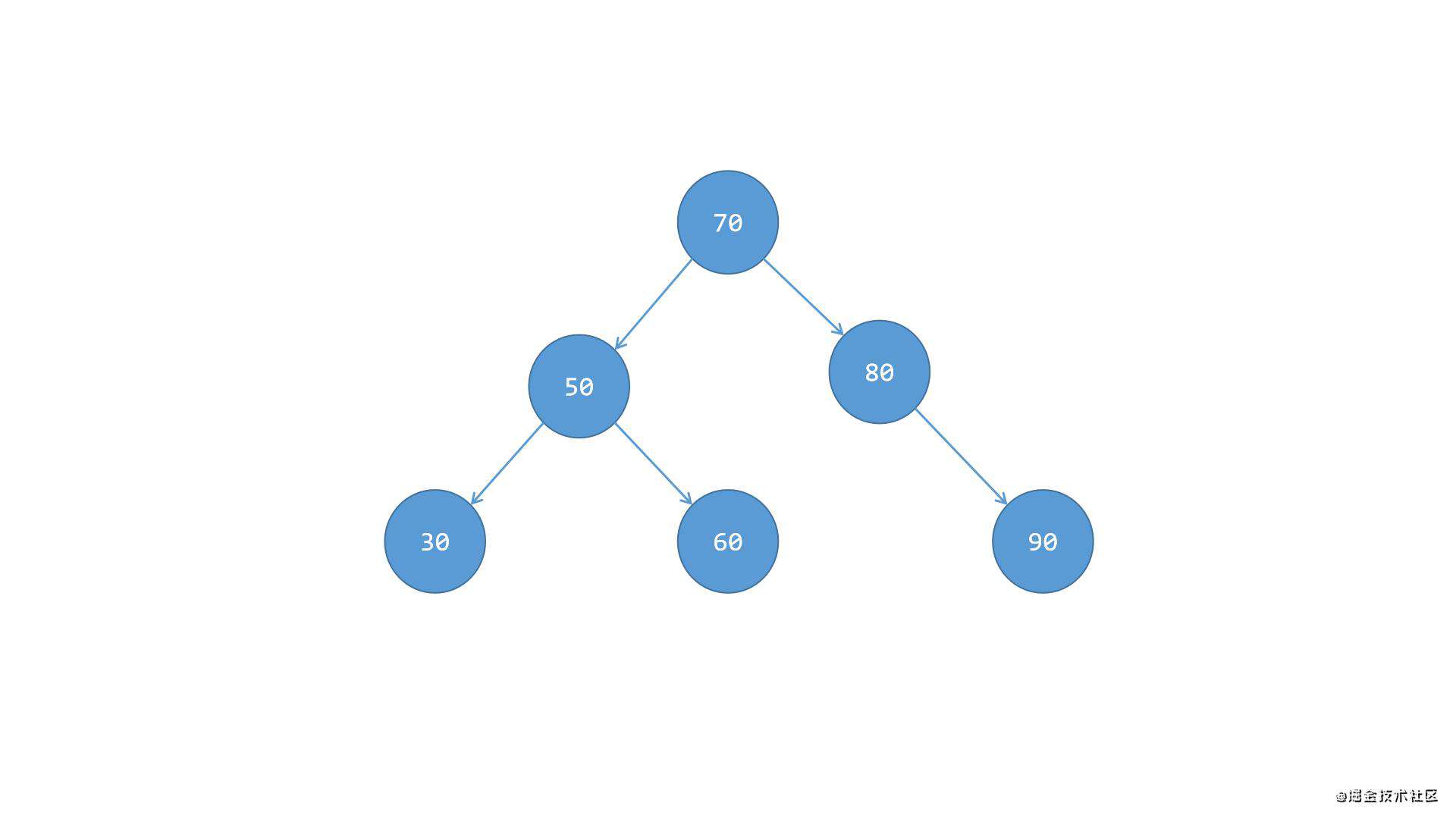
综上所述,RR使用场景为:节点的右侧子节点的高度大于左侧子节点的高度时,并且右侧子节点也是平衡或者右侧较重的情况。
场景三:
左右(LR):向右的双旋转(先LL向右的单旋转,再RR向左的单旋转)
此时又可细分为两种情况:
情况1:
节点的左偏重,左侧子节点的右侧子节点是平衡的,如下图所示:
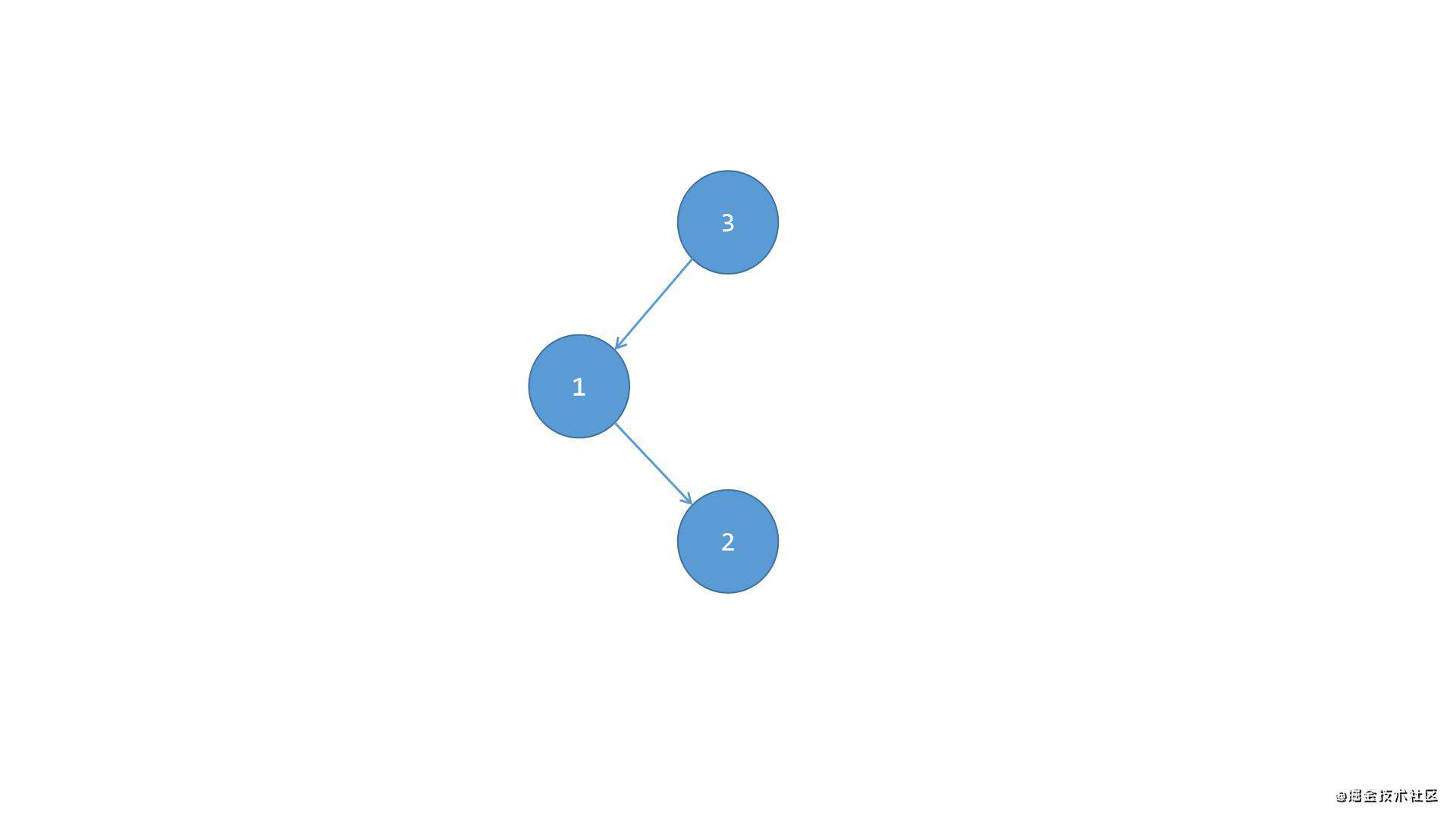
根节点3的左侧偏重,且左侧子节点1的右侧偏重,左侧子节点1的右侧子节点2下方没有子节点,所以节点2下方是平衡的,但是节点3、1、2整体是不平衡的,此时需要保持平衡的话:
第一步,先将节点2从原来的位置替换掉节点1的位置,并且将节点1变成节点2的左侧子节点,这样就变成了之前场景一(左左)中的情况1了,如下图所示:
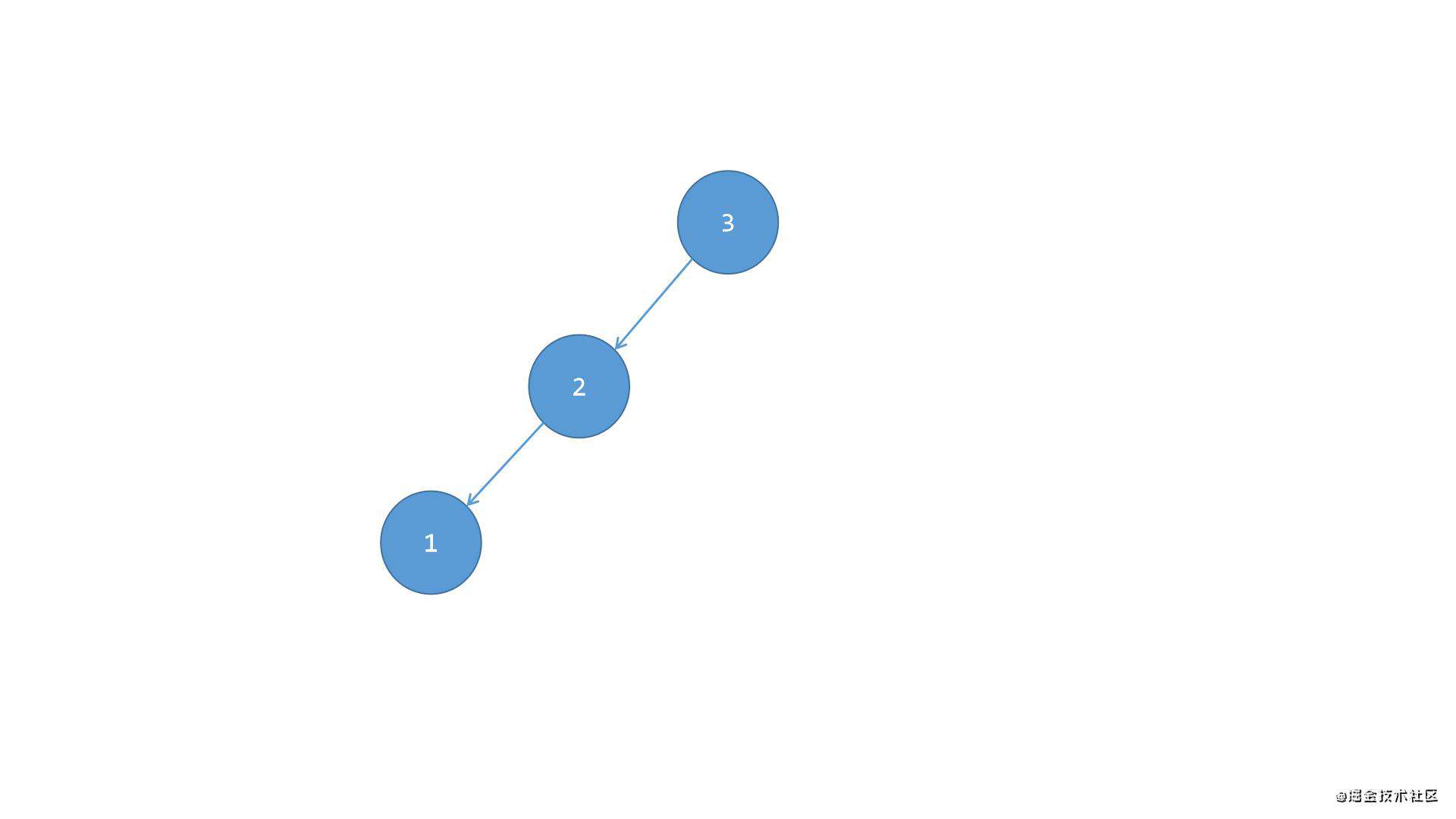
第二步,像之前场景一(左左)中的情况1那样,将根节点3进行向右的单旋转,成为节点2的右侧子节点即可保持平衡,如下图所示:
流程图如下:
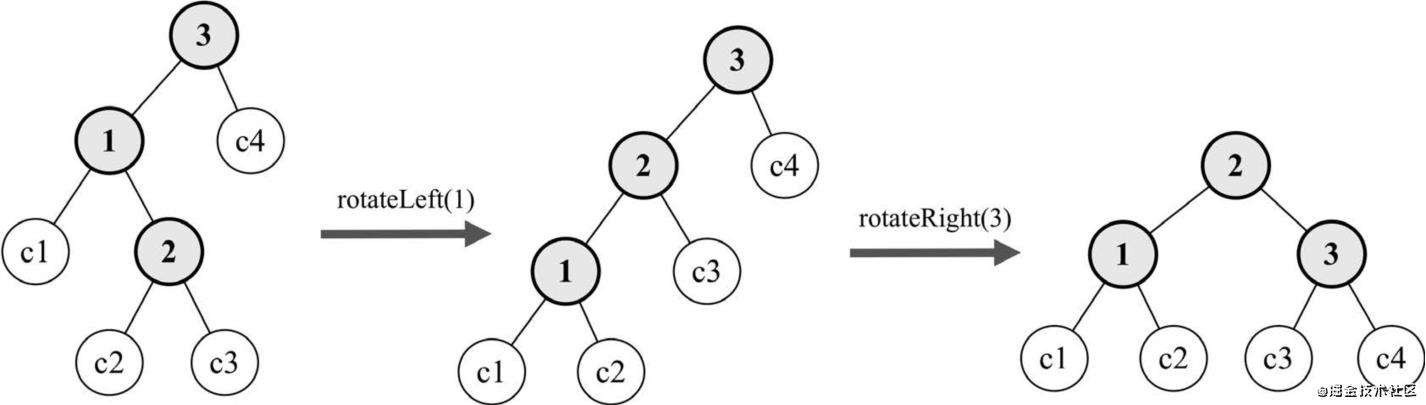
情况2:
节点的左侧子树偏重,左侧子树的右侧偏重,且左侧子树的右侧子节点的下方是不平衡的,如下图所示:
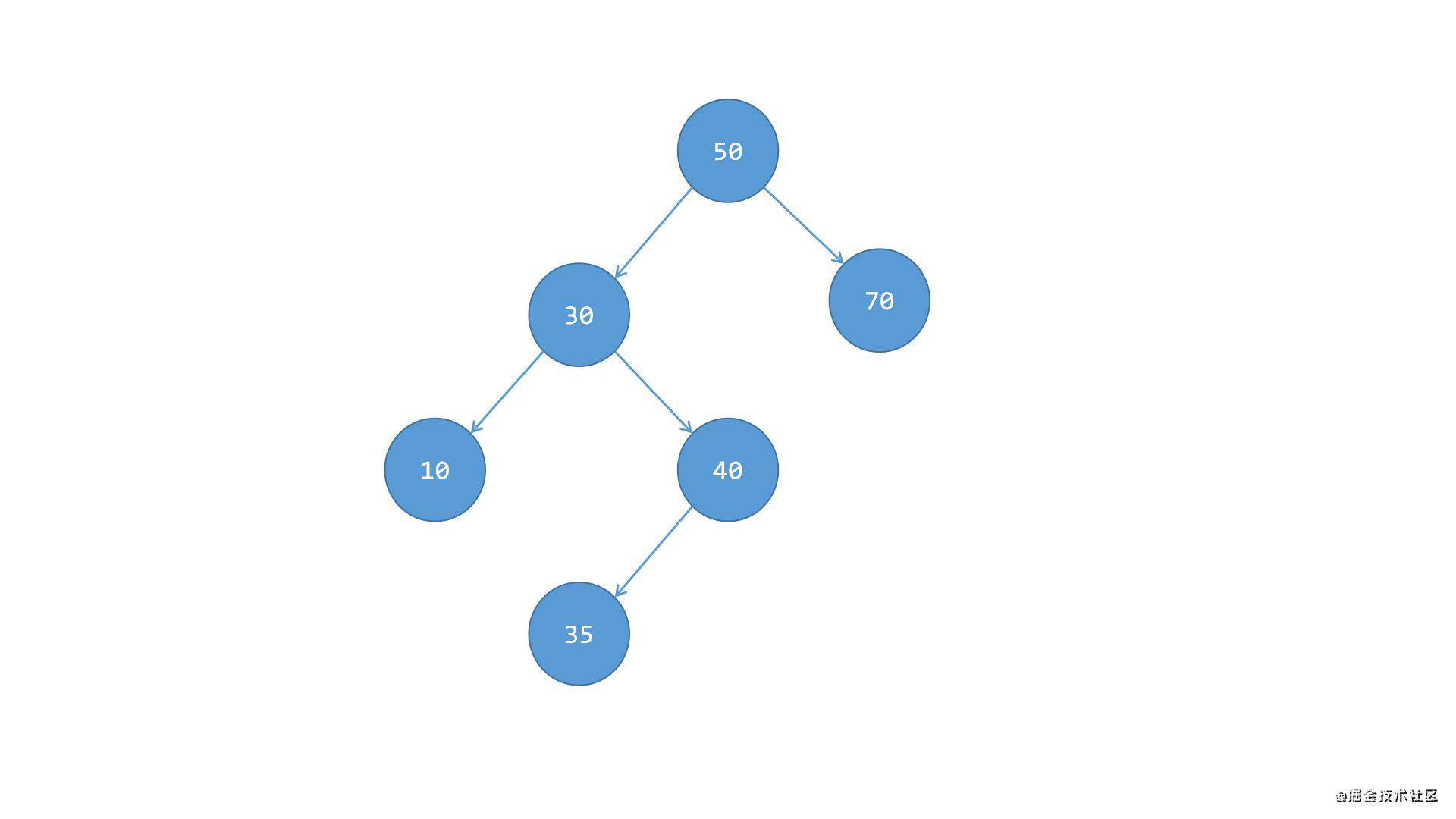
根节点50的左侧子树偏重,左侧子节点30的右侧子节点40的下方只有左边一侧有子节点35,所以此时子节点40是不平衡的,且整体也都是不平衡的,此时需要保持平衡的话:
第一步,先将根节点50与左侧子树分离,如下图所示:
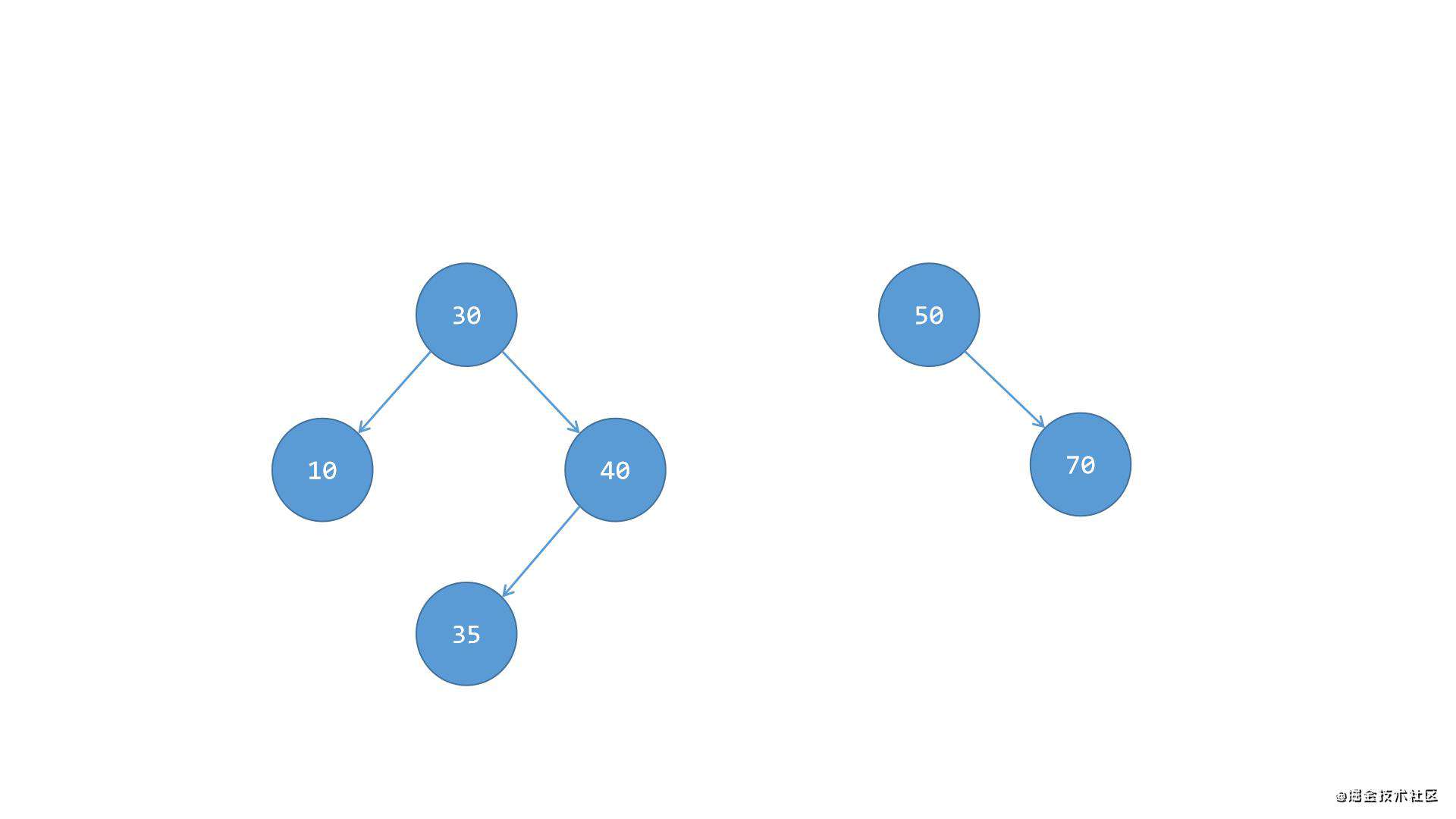
第二步,将节点40的左侧子节点35替换到节点40原来的位置,此时节点35成为节点30右侧的新子节点,然后将节点40变成节点30的父节点,如下图所示:
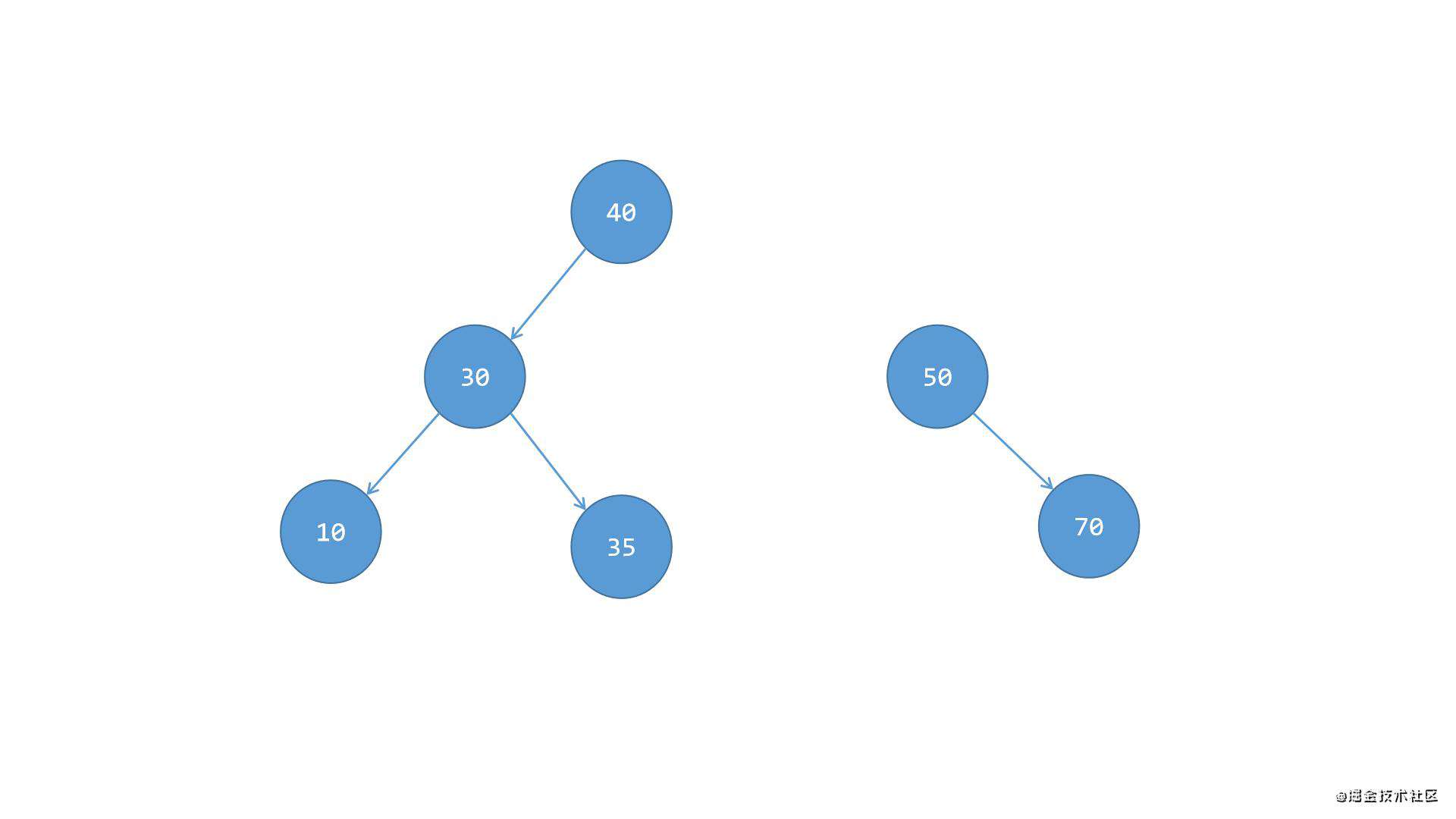
第三步,将节点40这一系整体作为根节点50的左侧子树,这样就又变成了之前场景一(左左)中的情况1了(我知道上一步直接将节点50这一系变成节点40的右侧子树就能直接平衡,但是变回场景一中的情况1有利于代码层面的复用),如下图所示:
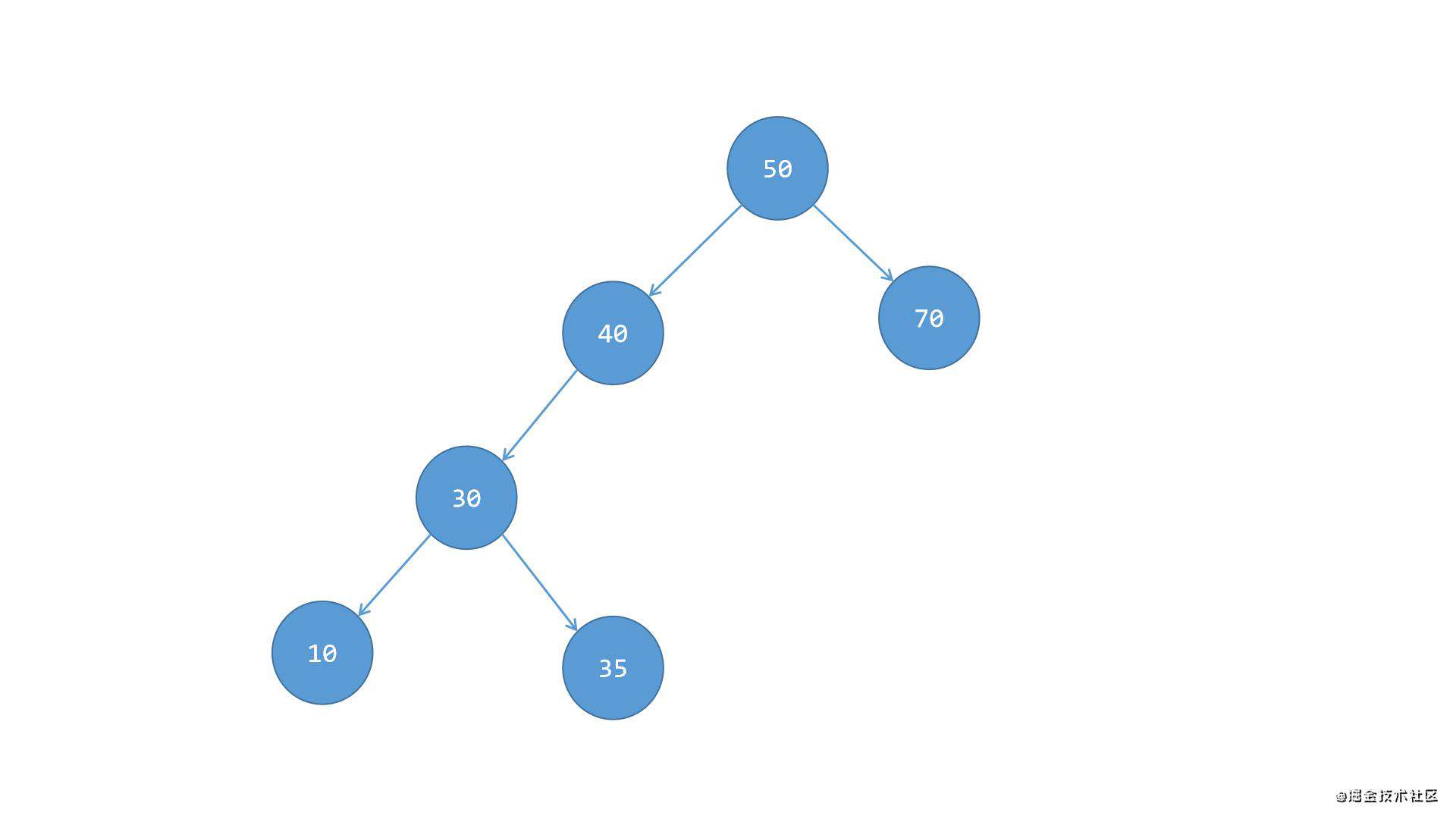
第四步,像之前场景一(左左)中的情况1那样,将根节点50连带着子节点70这一系整体进行向右的单旋转,作为节点40的右侧子树,这样整体就保持平衡,如下图所示:
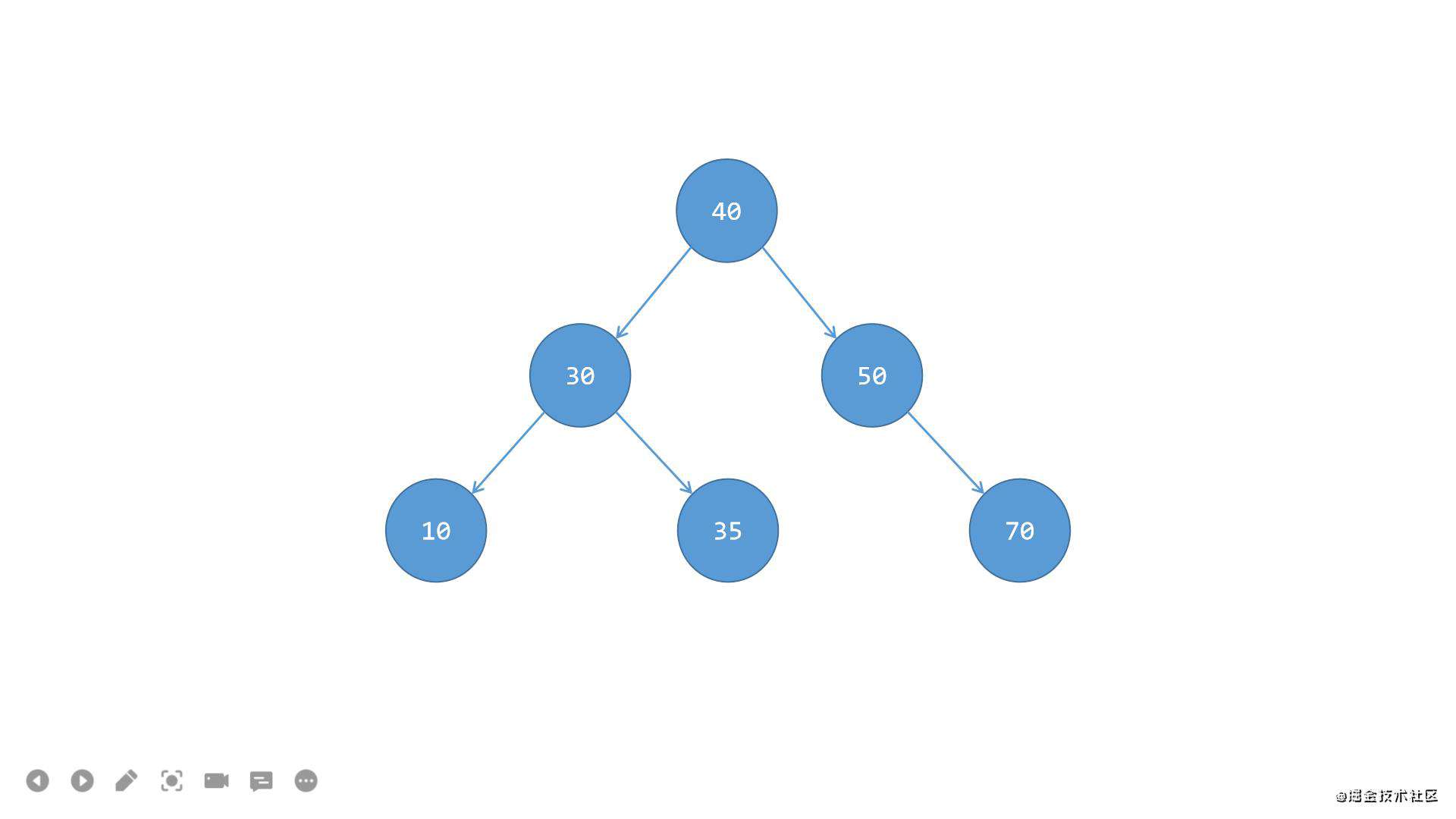
整体流程如下:
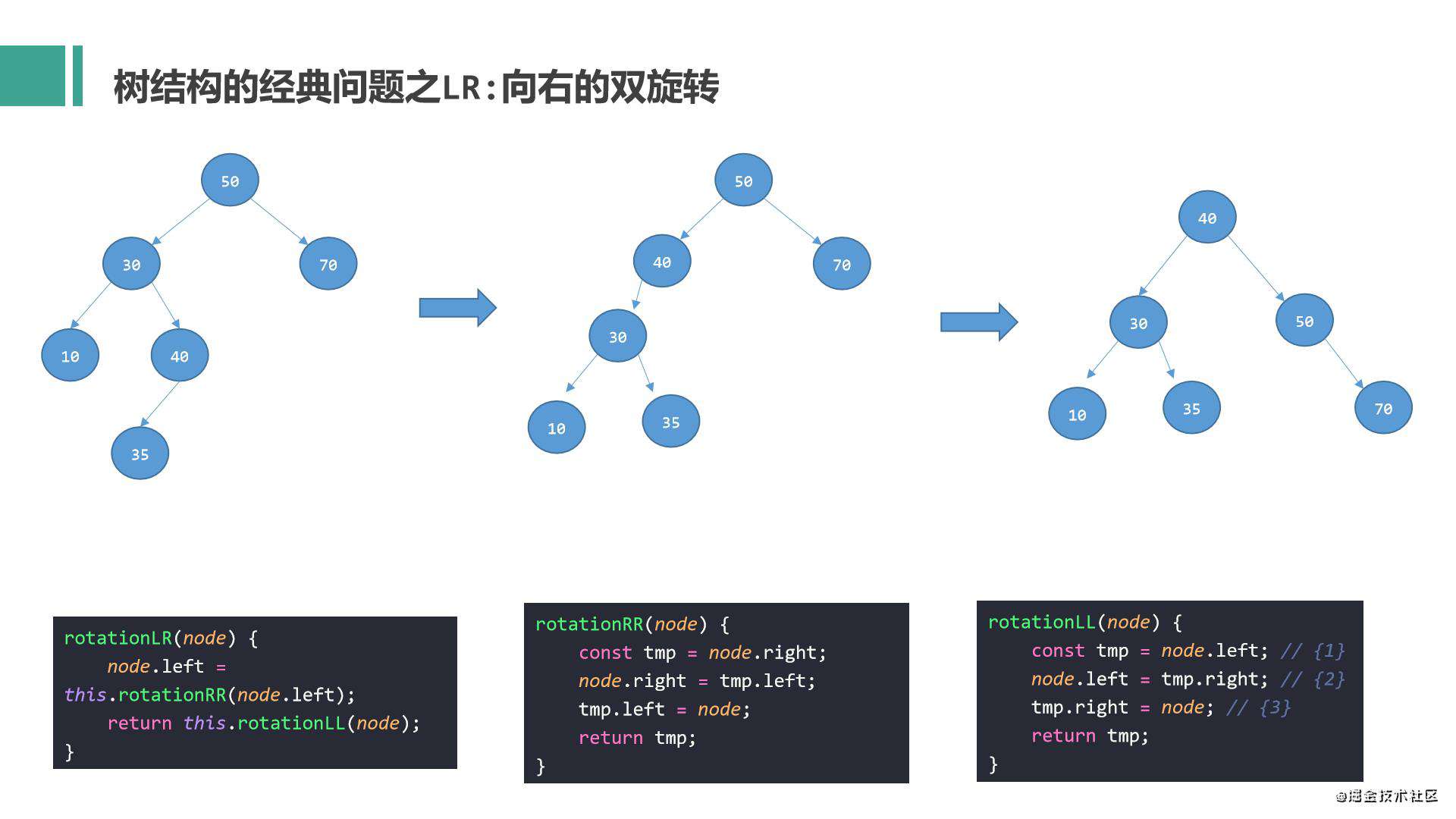
LR使用场景:节点的左侧子节点高度大于右侧子节点的高度,并且左侧子节点的右侧较重的情况。
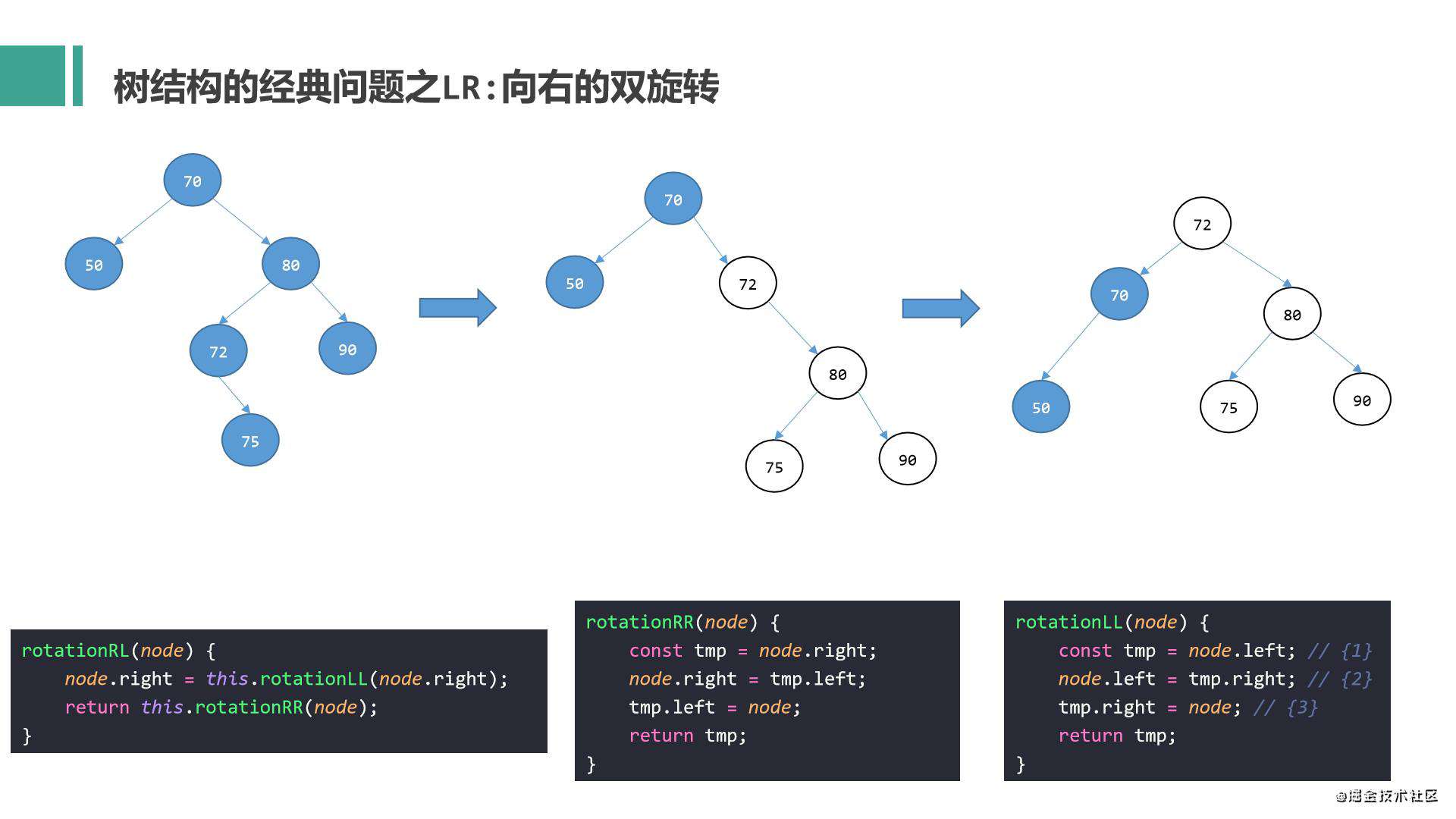
场景四:
右左(RL):向左的双旋转(先RR向左的单旋转,再LL向右的单旋转)
此时又可细分为两种情况:
情况1:
节点的右偏重,右侧子节点的左侧子节点是平衡的,如下图所示:
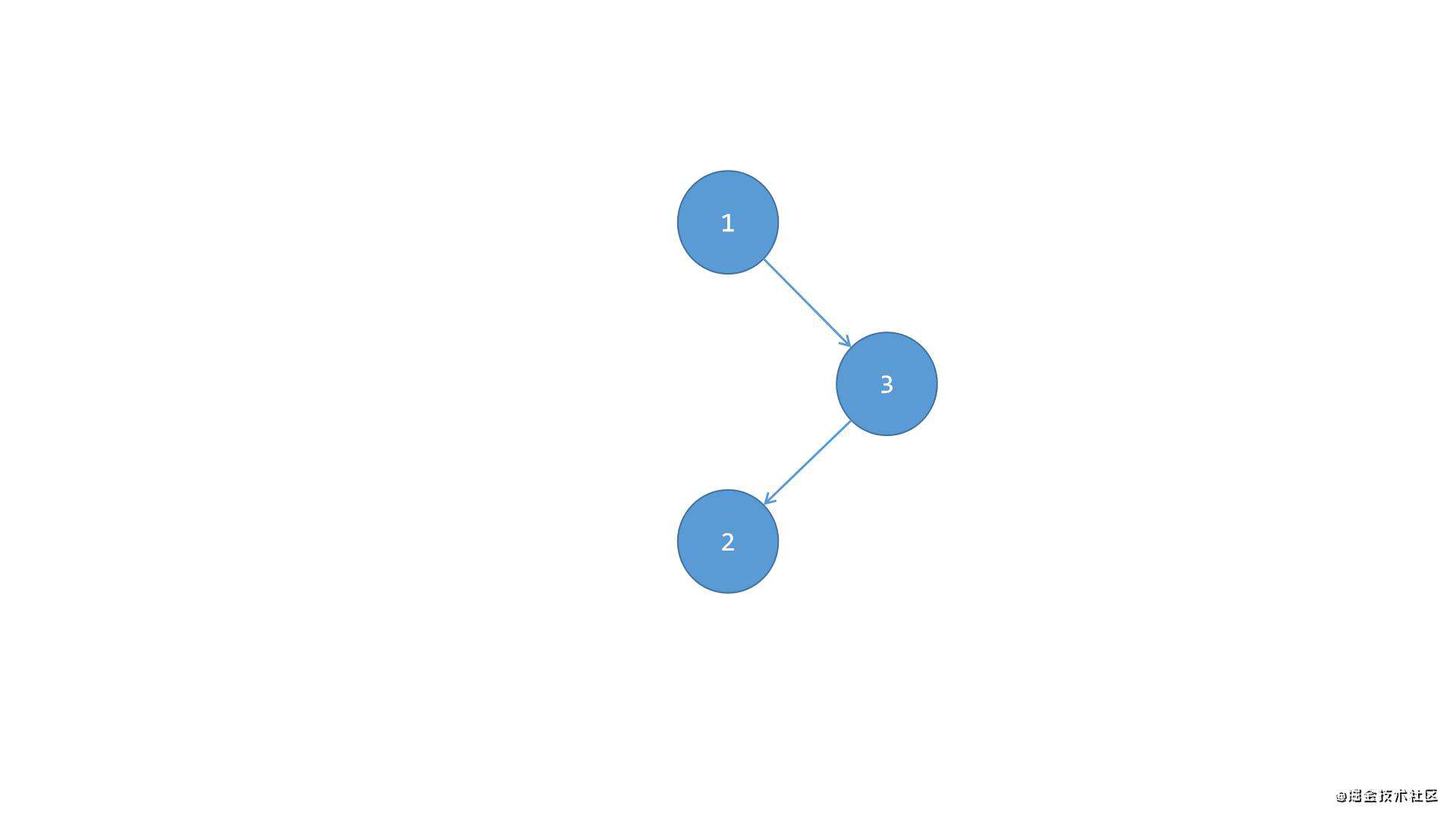
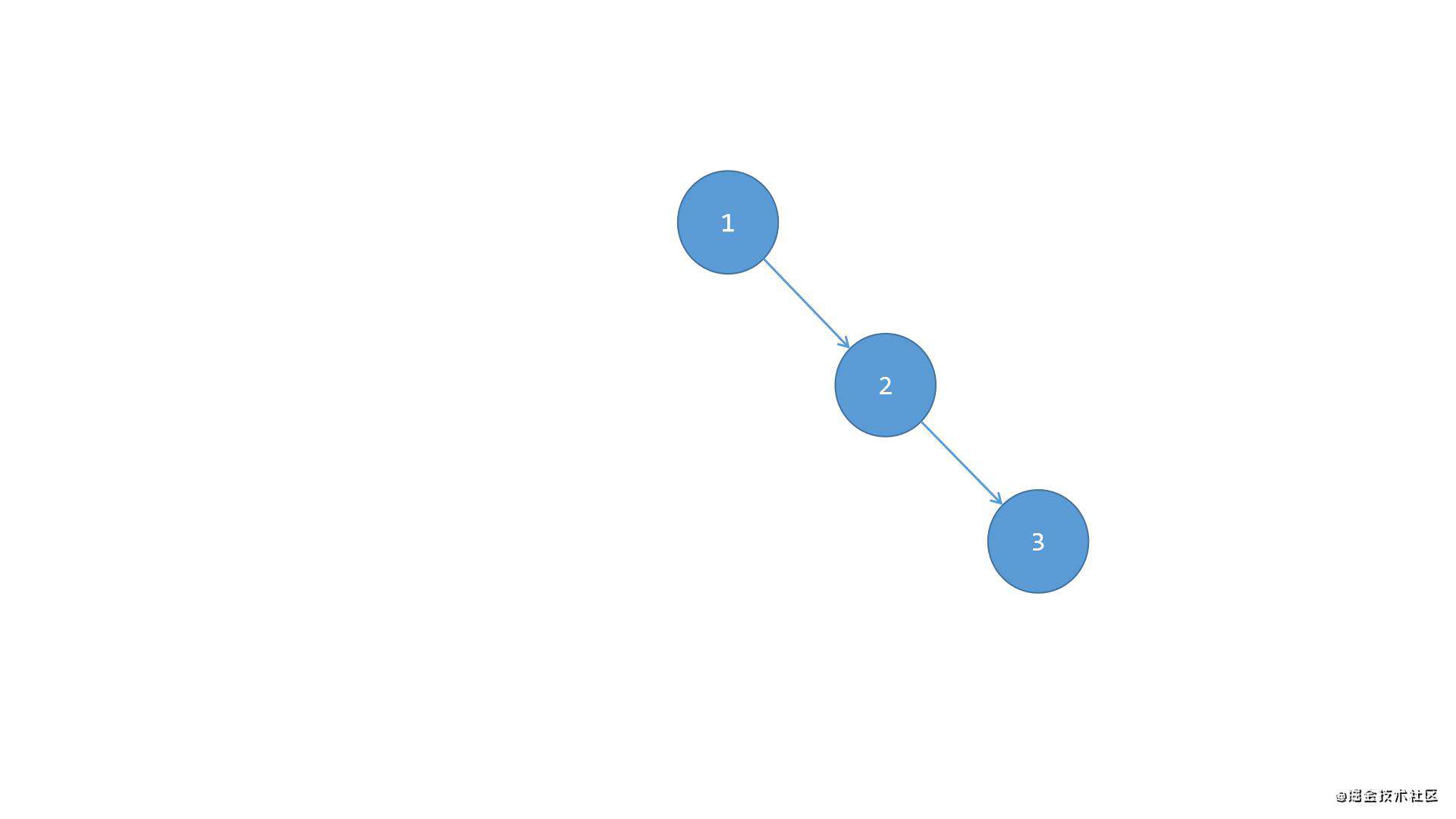
根节点1的右侧偏重,且右侧子节点3的左侧偏重,右侧子节点3的左侧子节点2下方没有子节点,所以节点2下方是平衡的,但是节点1、3、2整体是不平衡的,此时需要保持平衡的话:
第一步,先将节点2从原来的位置替换掉节点3的位置,并且将节点3变成节点2的右侧子节点,这样就变成了之前场景二(右右)中的情况1了,如下图所示:
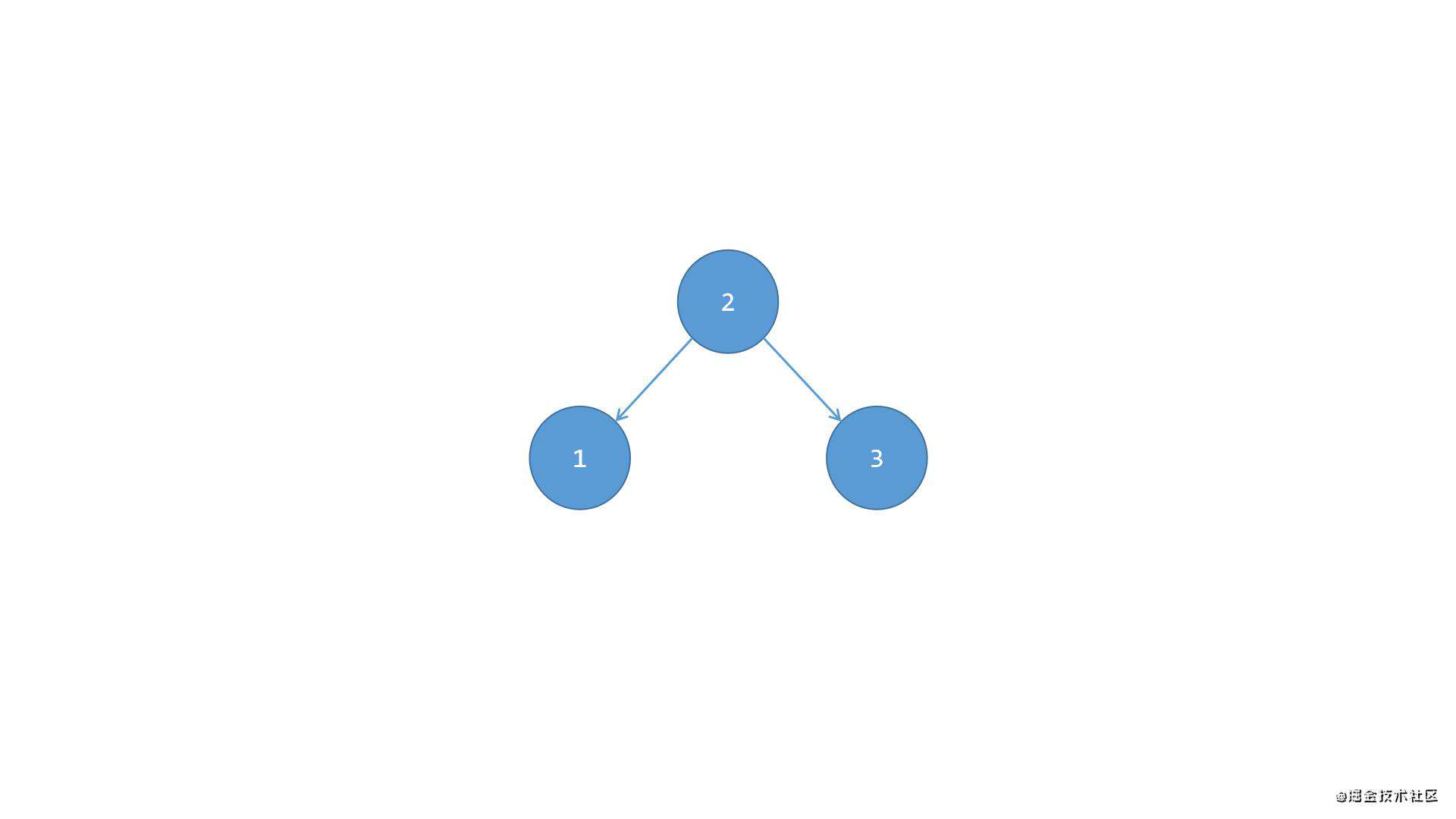
第二步,像之前场景二(右右)中的情况1那样,将根节点1进行向左的单旋转,成为节点2的左侧子节点即可保持平衡,如下图所示:
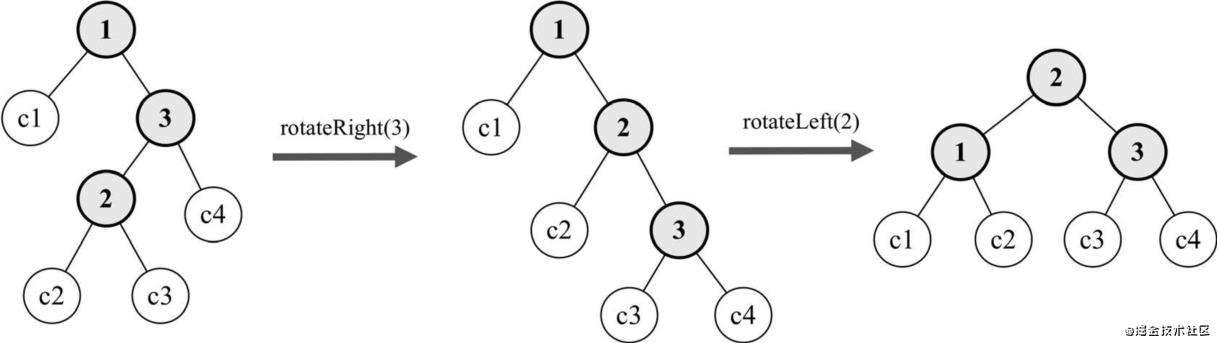
流程图如下:
情况2:
节点的右侧子树偏重,右侧子树的左侧偏重,且右侧子树的左侧子节点的下方是不平衡的,如下图所示:
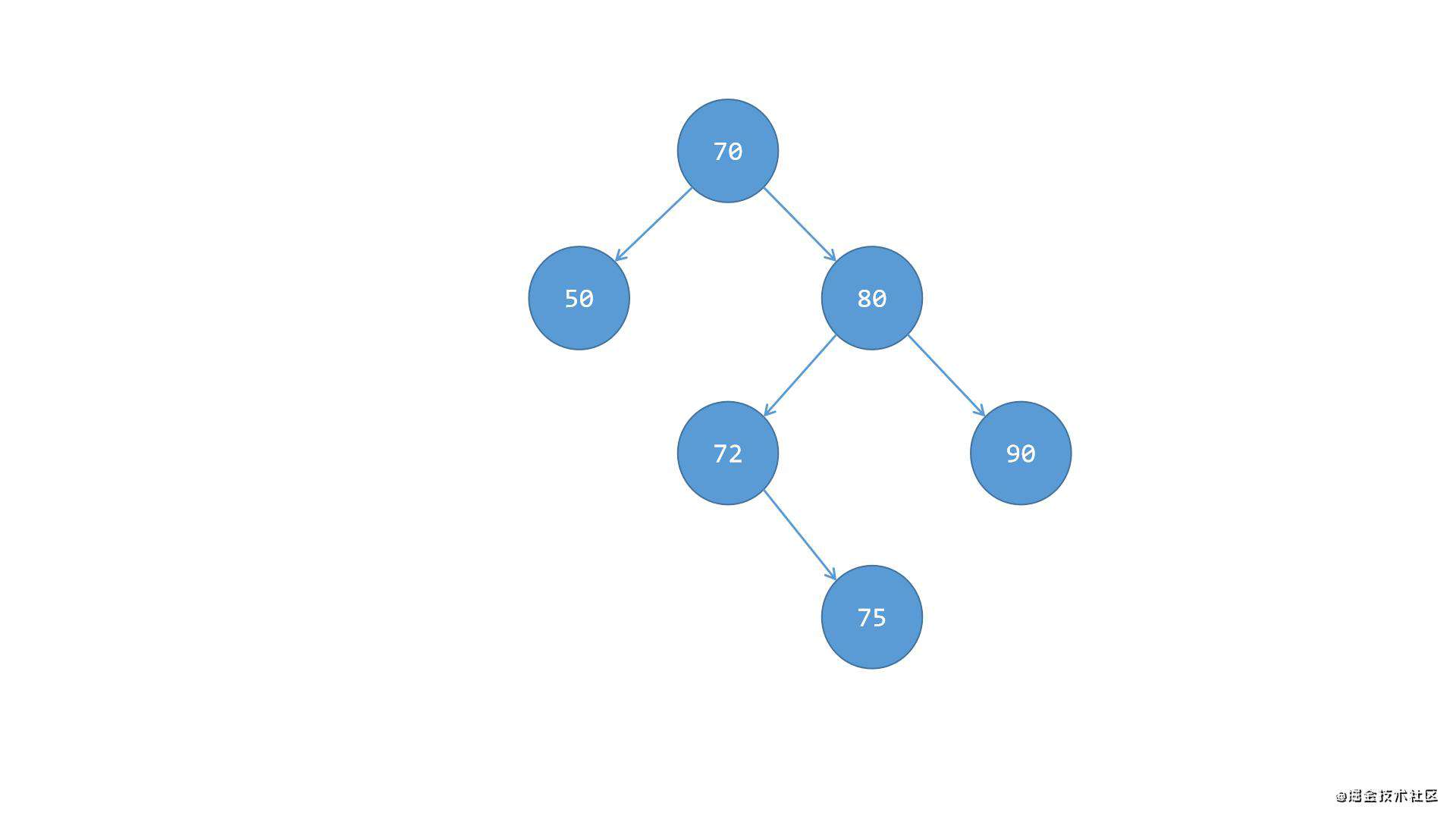
根节点70的右侧子树偏重,右侧子节点80的左侧子节点72的下方只有右边一侧有子节点75,所以此时子节点72是不平衡的,且整体也都是不平衡的,此时需要保持平衡的话:
第一步,先将根节点70与右侧子树分离,如下图所示:
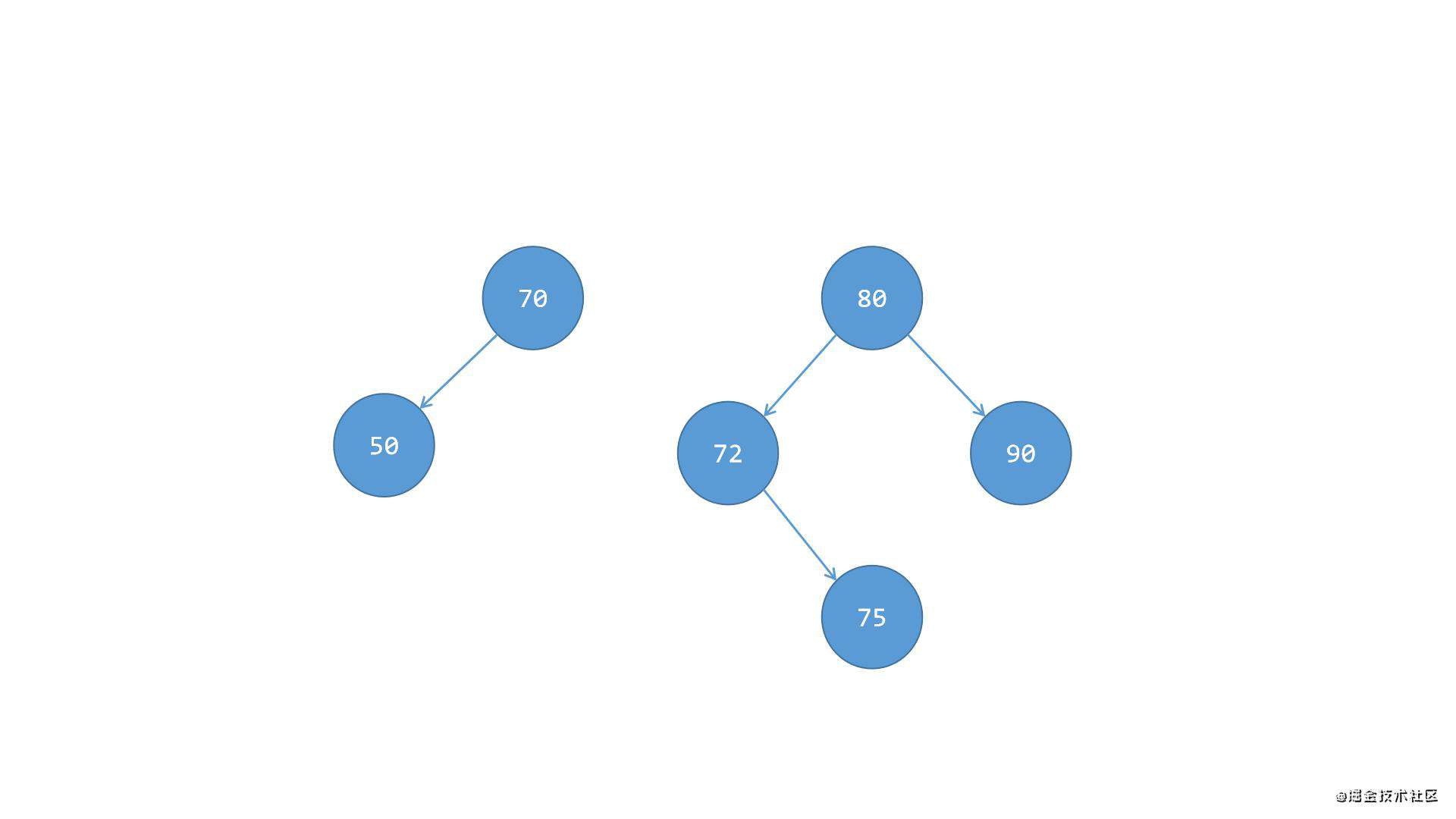
第二步,将节点72的右侧子节点75替换到节点72原来的位置,此时节点75成为节点80左侧的新子节点,然后将节点72变成节点80的父节点,如下图所示:
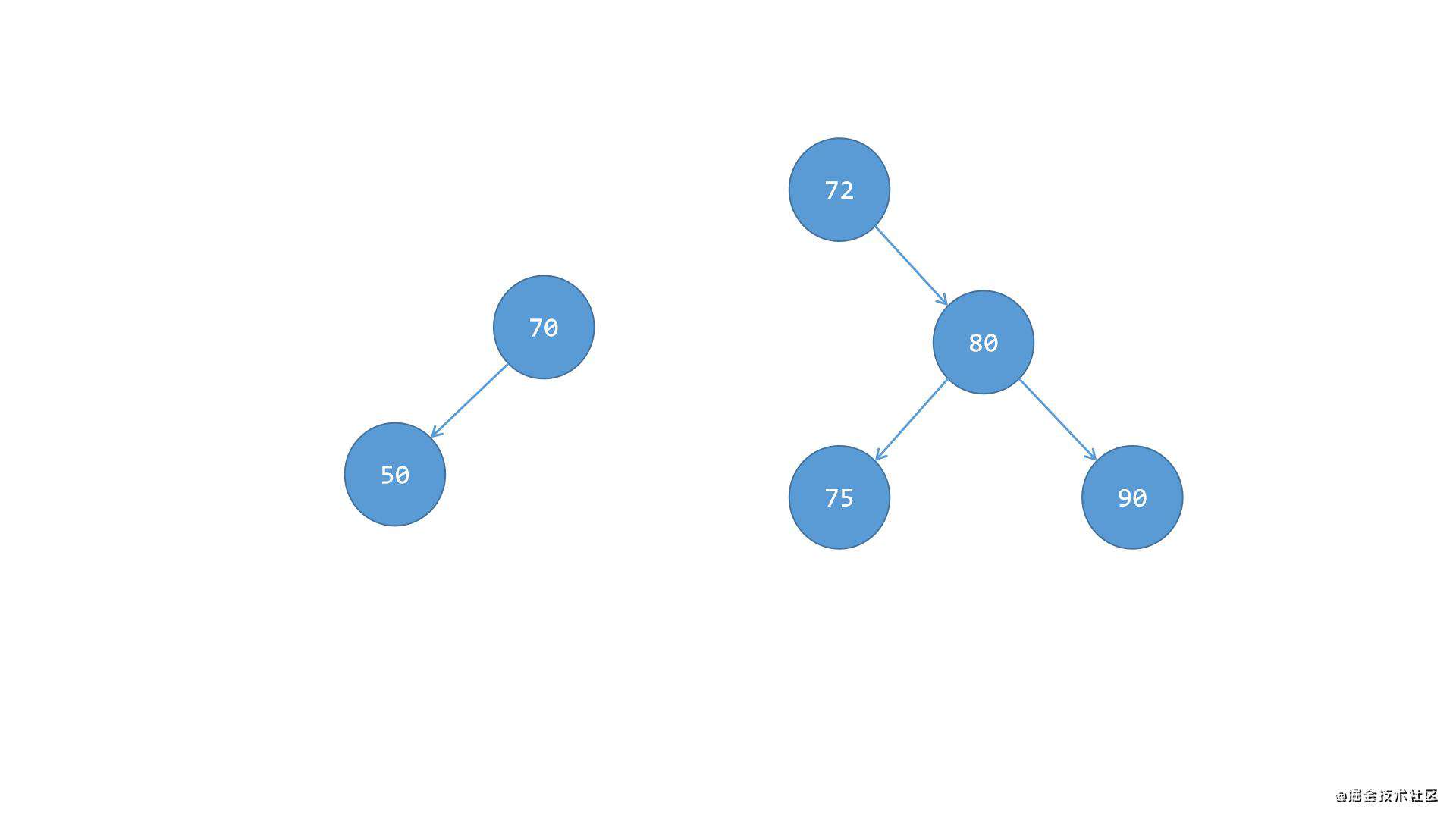
第三步,将节点72这一系整体作为根节点70的右侧子树,这样就又变成了之前场景二(右右)中的情况1了(我知道上一步直接将节点70这一系变成节点72的左侧子树就能直接平衡,但是变回场景二中的情况1有利于代码层面的复用),如下图所示:
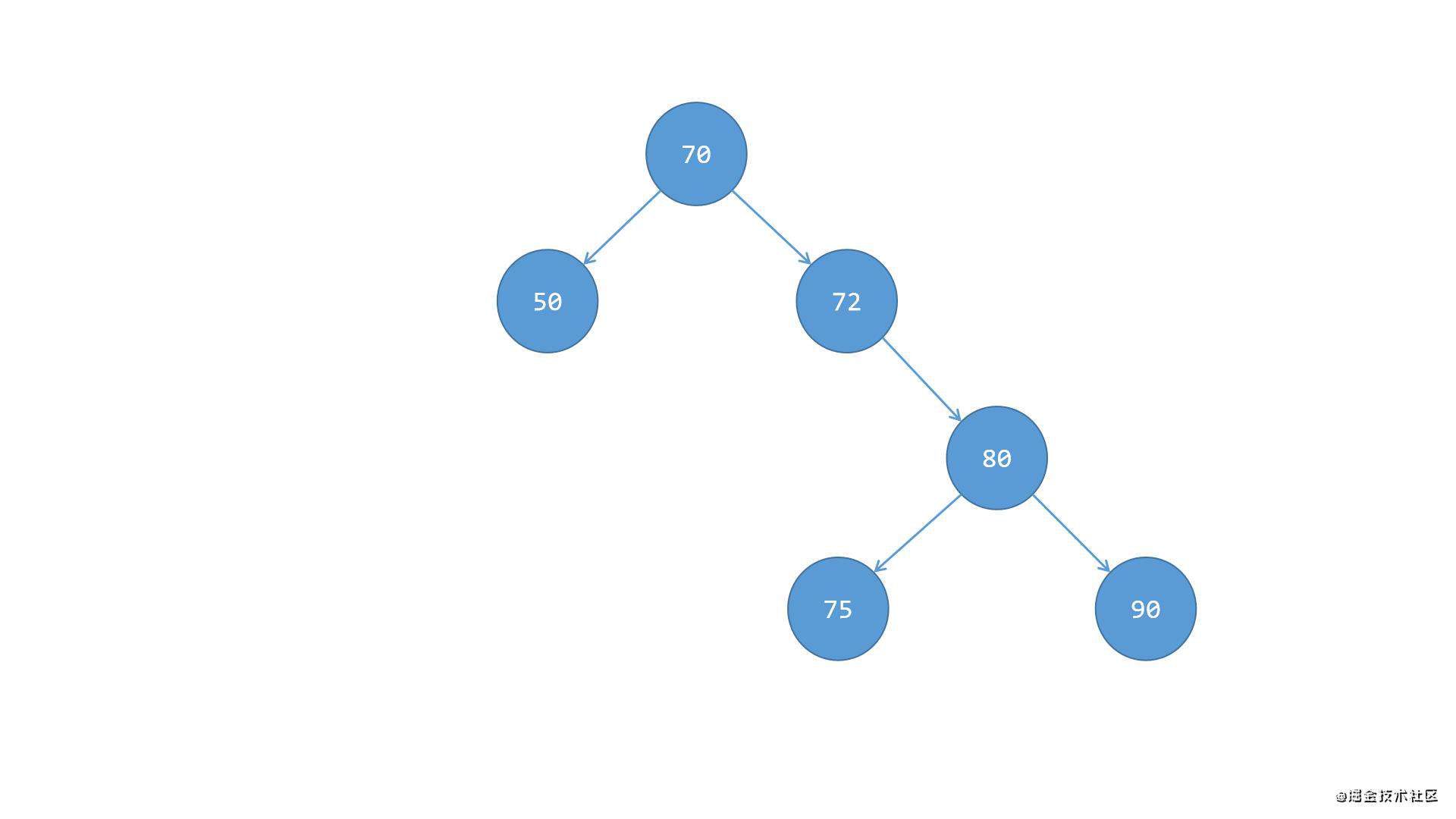
第四步,像之前场景二(右右)中的情况1那样,将根节点70连带着子节点50这一系整体进行向左的单旋转,作为节点72的左侧子树,这样整体就保持平衡,如下图所示:
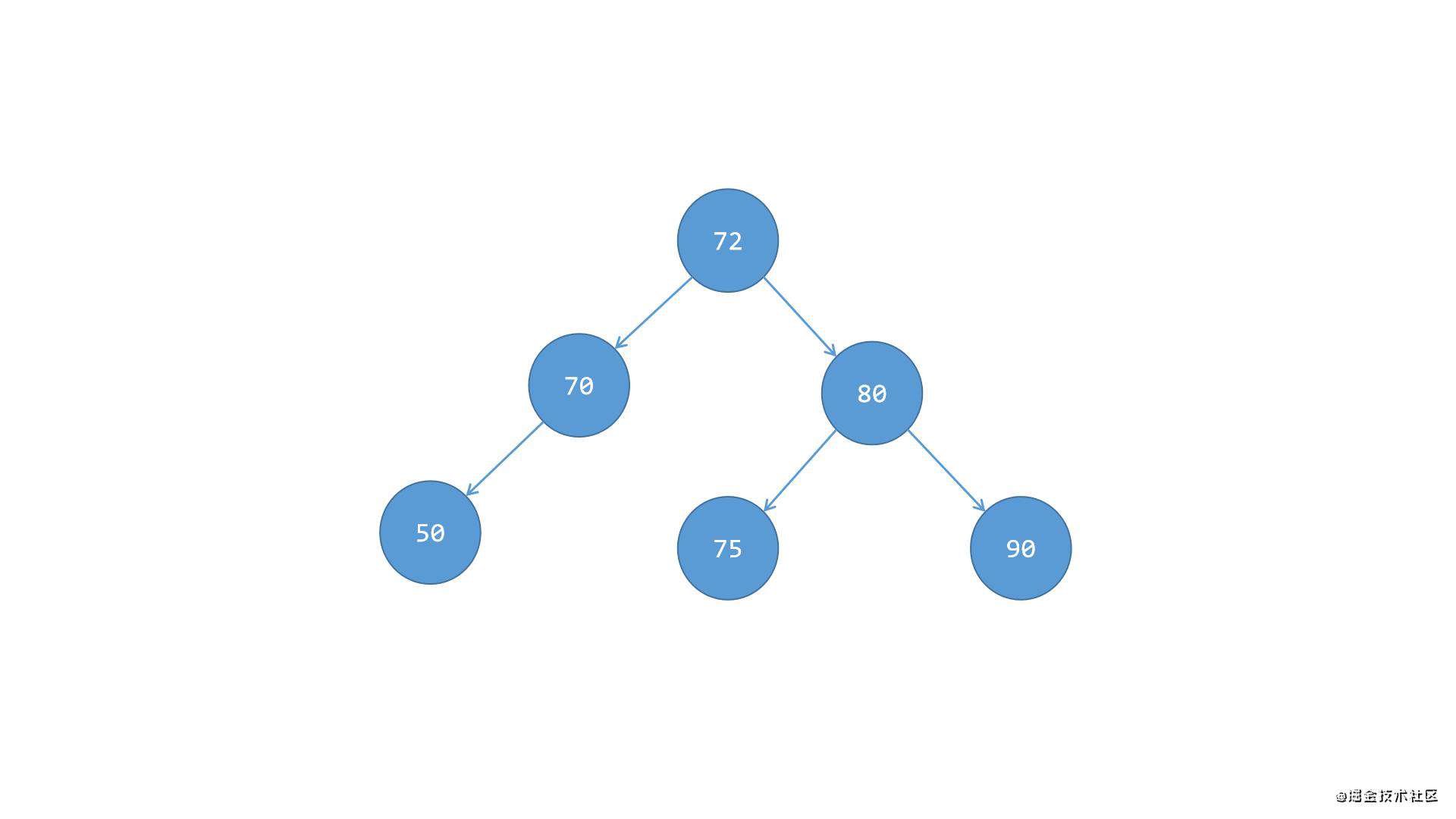
整体流程如下:
自平衡二叉树的自我实现
既然AVL树是一个BST树,我们可以扩展我们写的BST类,只需要覆盖用来维持AVL树平衡的方法,也就是insert、insertNode和removeNode方法。所有其他的BST方法将会被AVLTree类继承。
(如果代码看不懂,没太大关系,请千万要先把图中的转换看懂!用了一上午才做好的这些图,也不知道其他小伙伴能不能理解。)
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!