【前端算法系列】二叉树

二叉树的定义

二叉树的一般包含根节点、左子树和右子树。

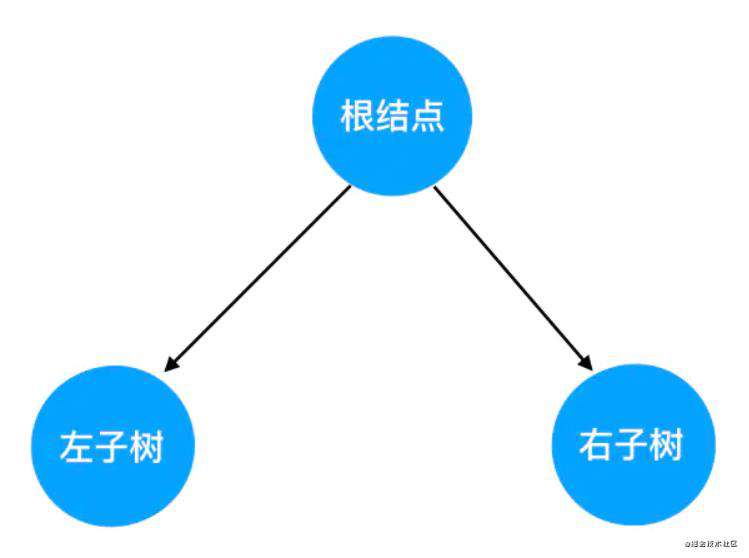
二叉树遍历

上图的二叉树，可以用代码表示如下：

const root = {
  val: "根节点",
  left: {
    val: "左子树",
    left: null,
    right: null
  },
  right: {
    val: "右子树",
    left: null,
    right:null
  }
};

所谓遍历就是把树结构的数据，转化成数组或者其他形式的数据输出出来，例如上面的树代码，前序遍历的结果就是：['根节点','左子树','右子树']。

二叉树的遍历通常有3 + 1种方式，分别是前序序遍历、中序遍历、后序遍历和层序遍历。前三种遍历是DFS（深度优先搜索），最后一种遍历是BFS（广度优先搜索）。

前序遍历

二叉树的前序遍历的顺序是：根结点 -> 左子树 -> 右子树

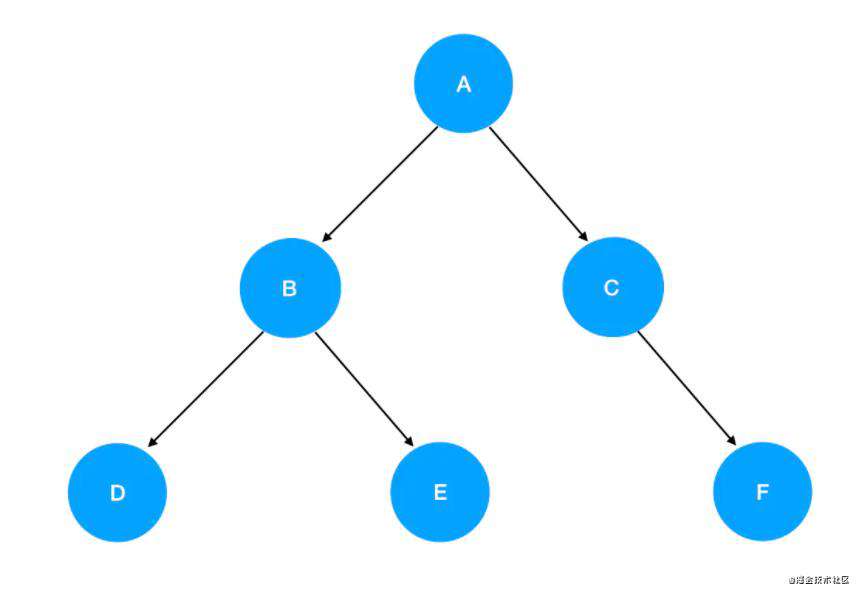
上图所示的树，前序遍历的结果是：[A,B,D,E,C,F]

二叉树前序遍历的JavaScript实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
// 递归解法
var preorderTraversal = function(root) {
    var res = []
    const preorder = (root)=>{
        if(!root){
            return
        }
        res.push(root.val)
        preorder(root.left)
        preorder(root.right)
    }
    preorder(root)
    console.log(res)
    return res
};

// 迭代法
var preorderTraversal = function(root) {
    var res = []
    if(!root){
        return res
    }
    var stack = []
    stack.push(root)
    while(stack.length){
        var cur = stack.pop(); // 取出栈顶元素(先序遍历：root --> left --> right)
        res.push(cur.val)

        if(cur.right){ // 右子树入栈
            stack.push(cur.right)
        }

        if(cur.left){ // 左子树入栈
            stack.push(cur.left)
        }
    }
    return res
};

中序遍历

二叉树的中序遍历是：左子树 -> 根结点 -> 右子树

上图所示的二叉树，中序遍历的结果是:[D,B,E,A,C,F]。

二叉树中序遍历的JavaScript实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
// 递归法
var inorderTraversal = function(root) {
    var res = []

    var inorder = (root)=>{
      if(!root) {
           return
      }
      
      inorder(root.left)
      
      res.push(root.val)
      
      inorder(root.right)
    }
    inorder(root)
    return res
};

// 迭代法
var inorderTraversal = function(root) {
    var res = [], // 定义结果数组
        stack = [], // 初始化栈结构
        cur = root; // 当前遍历的节点

    // 当cur有值或栈不为空时，继续循环
    while(cur || stack.length){
        // 循环查找左节点，直至最后一个节点，并保存中途经过的节点
        while(cur){
            stack.push(cur) // cur值入栈
            cur = cur.left // 继续遍历左节点的值
        }

        cur = stack.pop() // 取出栈顶元素，即最左边的节点
        res.push(cur.val) // 将栈顶元素保存至结果数组
        cur = cur.right // 尝试循环右边节点，此时cur的所有左节点已经在栈中
    }
  
    return res
};

后序遍历

二叉树的后序遍历是：左子树 -> 右子树 -> 根结点

上图所示的二叉树，后序遍历的结果是:[D,E,B,F,C,A]，值得注意的是，后序遍历时，首先遍历的也是根节点（而不是先从最左边的节点开始遍历）。

二叉树后序遍历的JavaScript实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */

// 递归法
var postorderTraversal = function(root) {
    var res = []
    var postorder = (root)=>{
        if(!root){
            return
        }
        postorder(root.left)
        postorder(root.right)
        res.push(root.val)
    }
    postorder(root)
    return res
};

// 迭代法
var postorderTraversal = function (root) {
    var res = []

    if (!root) {
        return res
    }

    var stack = []

    stack.push(root)
    /**
     * 解释一下这个while循环：
     * 第一次循环，root节点入栈（stack:[root]），取root的值并放入res栈底（res：[root]），
     * 接着是左右节点分别入栈 （stack:[right,left]）；
     * 进入下一次循环，stack中的右节点出栈，取值并放入res栈底（res：[right,root]）,
     * stack中的左节点出栈，取值放入res栈底（res:[left,right,root]），
     * 一层循环结束，res栈中的数据就是第一次循环的结果。
     * 继续循环，最终得出二叉树的后序遍历结果。
     *  */
    while (stack.length) { // 后序遍历：left --> right --> root
        var cur = stack.pop(); //  取出栈顶元素

        res.unshift(cur.val) // 当前节点放入结果栈底

        if (cur.left) { // 左节点入栈
            stack.push(cur.left)
        }

        if (cur.right) { // 右节点入栈
            stack.push(cur.right)
        }
    }
    return res
};

层序遍历

二叉树的层序遍历是广度优先搜索(BFS)，遍历的顺序为：根节点 -> 第N层节点 -> 最后一层节点。

如下，二叉树

    3
   / \
  9  20
    /  \
   15   7

其层序遍历为：

[
  [3],
  [9,20],
  [15,7]
]

层序遍历的JavaScript实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
    var res = []
    if (!root) {
        return res
    }
    // 广度优先算法
    var BFS = (root) => {
        var queue = [] // 初始化一个队列
        queue.push(root)
        while (queue.length) { // 每次循环的队列，装的是一层的所有数据
            var level = [] // 本层的数据
            var qLen = queue.length // 缓存队列的长度，因为接下来的操作会改变队列的长度
            for (var i = 0; i < qLen; i++) {
                var top = queue.shift() // 取出队列中的第一个元素

                level.push(top.val) // 保存取出的数据

                if (top.left) {
                    queue.push(top.left)
                }
                if (top.right) {
                    queue.push(top.right)
                }
            }
            res.push(level)
        }
    }
    BFS(root)
    return res
};

特殊二叉树

特殊二叉树是二叉树的变种，包括二叉搜索树（又叫二叉查找树）、平衡二叉树、堆结构等。

二叉搜索树

二叉搜索树（Binary Search Tree）简称 BST，是二叉树的一种特殊形式。它有很多别名，比如排序二叉树、二叉查找树等等。二叉搜索树上的每一棵子树，都应该满足 左孩子 <= 根结点 <= 右孩子 这样的大小关系。下图我给出了几个二叉搜索树的示例：

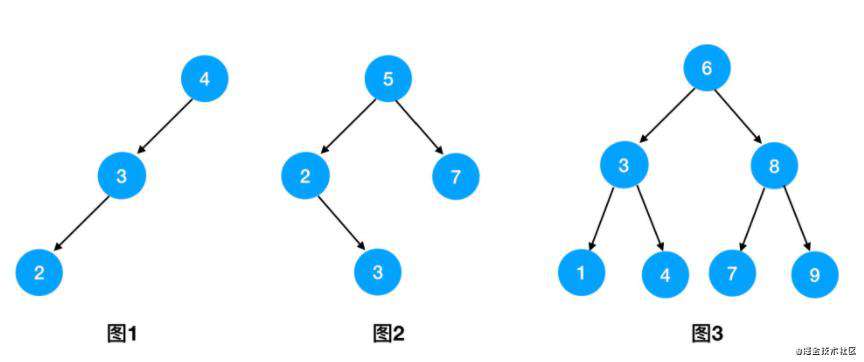
关于二叉搜索树的特性，有且仅有一条是需要大家背诵默写的： 二叉搜索树的中序遍历序列是有序的！

二叉搜索树验证

在不考虑相等节点的情况下，可以

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
const isValidBST = function(root) {
  // 定义递归函数
  function dfs(root, minValue, maxValue) {
      // 若是空树，则合法
      if(!root) {
          return true
      }
      // 若右孩子不大于根结点值，或者左孩子不小于根结点值，则不合法
      if(root.val <= minValue || root.val >= maxValue) return false
      // 左右子树必须都符合二叉搜索树的数据域大小关系
      return dfs(root.left, minValue,root.val) && dfs(root.right, root.val, maxValue)
  }
  // 初始化最小值和最大值为极小或极大
  return dfs(root, -Infinity, Infinity)
};

将排序数组转化成二叉搜索树

/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
const sortedArrayToBST = function(nums) {
    // 处理边界条件
    if(!nums.length) {
        return null
    }
    
    // root 结点是递归“提”起数组的结果
    const root = buildBST(0, nums.length-1)

    // 定义二叉树构建函数，入参是子序列的索引范围
    function buildBST(low, high) {
        // 当 low > high 时，意味着当前范围的数字已经被递归处理完全了
        if(low > high) {
            return null
        }
        // 二分一下，取出当前子序列的中间元素
        const mid = Math.floor(low + (high - low)/2)  
        // 将中间元素的值作为当前子树的根结点值
        const cur = new TreeNode(nums[mid]) 
        // 递归构建左子树，范围二分为[low,mid)
        cur.left = buildBST(low,mid-1)
        // 递归构建右子树，范围二分为为(mid,high]
        cur.right = buildBST(mid+1, high)
        // 返回当前结点
        return cur
    }
    // 返回根结点
    return root
};

平衡二叉树

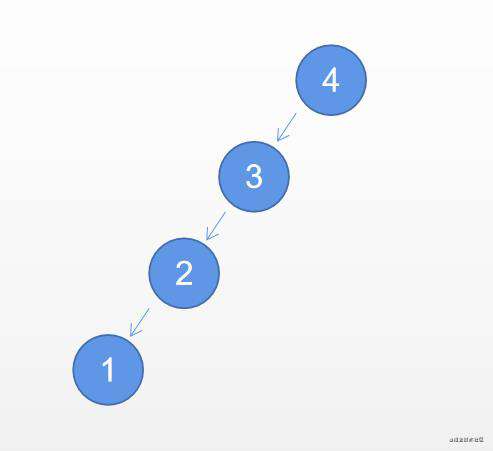
大家知道，对于同样一个遍历序列，二叉搜索树的造型可以有很多种。拿 [1,2,3,4]这个中序遍历序列来说，基于它可以构造出的二叉搜索树就包括以下两种造型：

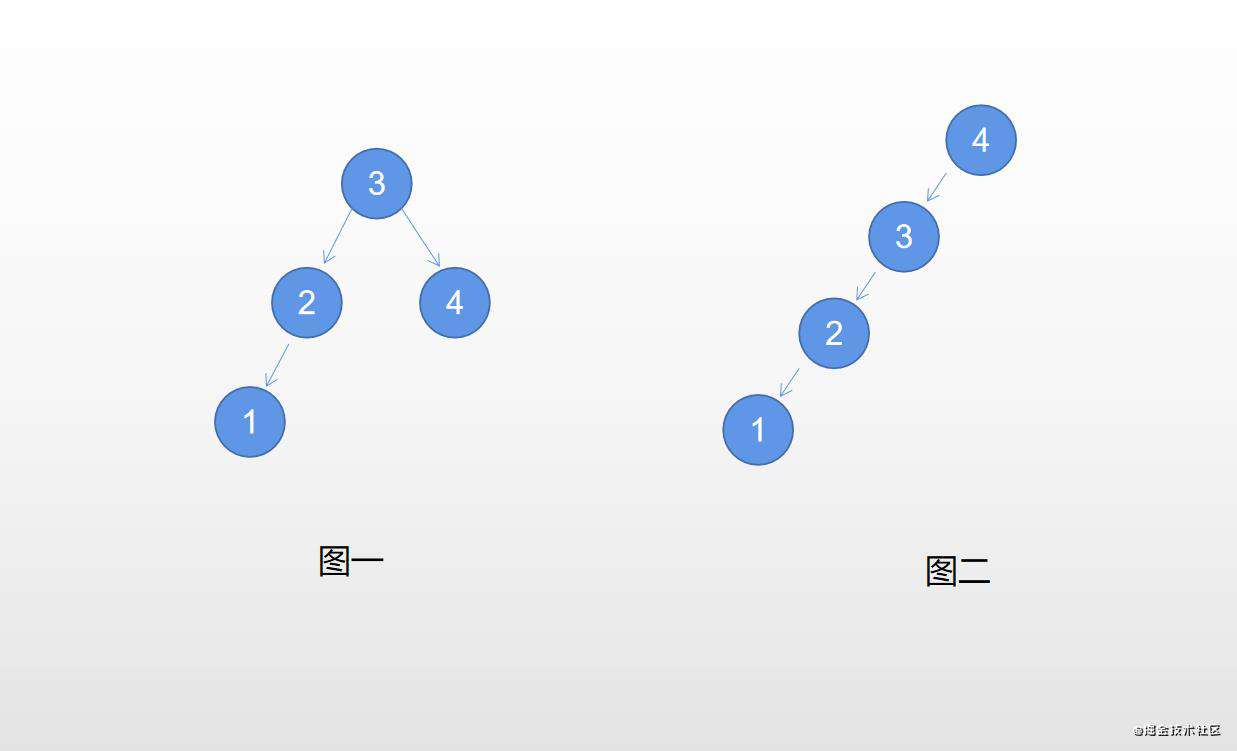
图一是平衡二叉树，图二是普通二叉树。假设现在要查找1这个元素，图一只要查找3次就可以找到，而图二要查找4次。

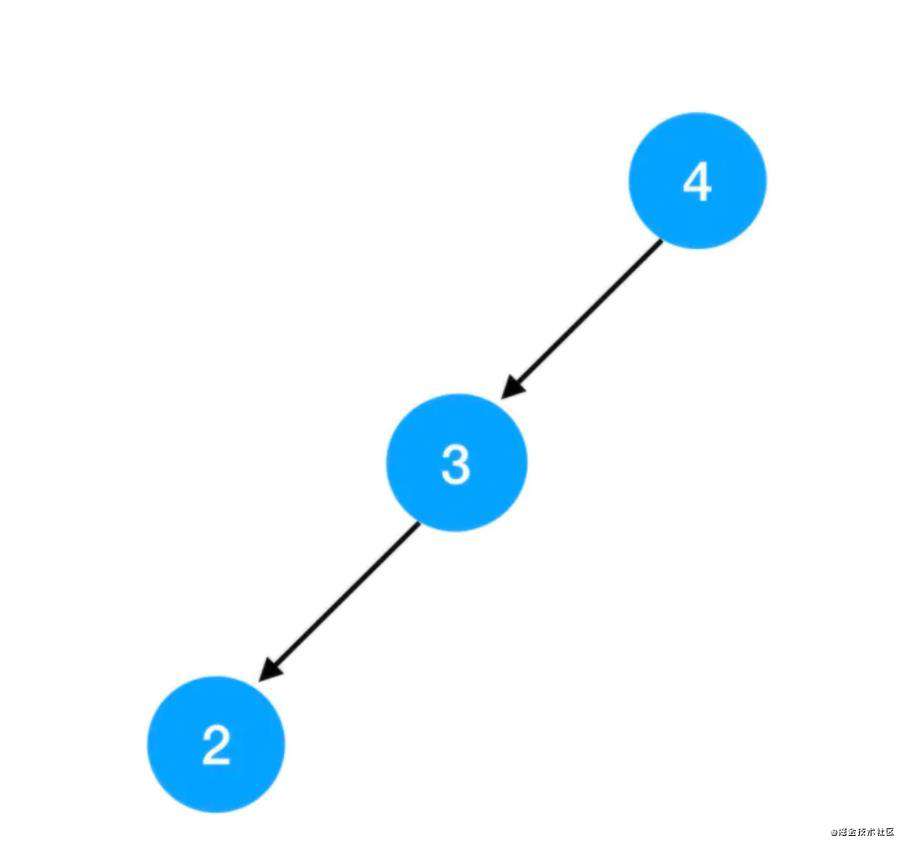
二叉搜索树的妙处就在于它把“二分”这种思想以数据结构的形式表达了出来。在一个构造合理的二叉搜索树里，我们可以通过对比当前结点和目标值之间的大小关系，缩小下一步的搜索范围（比如只搜索左子树或者只搜索右子树），进而规避掉不必要的查找步骤，降低搜索过程的时间复杂度。但是如果二叉搜索树的平衡度很低，例如下图：

查找元素时，会遍历很多空节点，带来高达O(N)的时间复杂度，而平衡二叉树由于利用了二分思想，查找操作的时间复杂度仅为 O(logN)。因此，为了保证二叉搜索树能够确实为查找操作带来效率上的提升，我们有必要在构造二叉搜索树的过程中维持其平衡度，这就是平衡二叉树的来由。

平衡二叉树的判定

const isBalanced = function(root) {
  // 立一个flag，只要有一个高度差绝对值大于1，这个flag就会被置为false
  let flag = true
  // 定义递归逻辑
  function dfs(root) {
      // 如果是空树，高度记为0；如果flag已经false了，那么就没必要往下走了，直接return
      if(!root || !flag) {
          return 0 
      }
      // 计算左子树的高度
      const left = dfs(root.left)  
      // 计算右子树的高度
      const right = dfs(root.right)  
      // 如果左右子树的高度差绝对值大于1，flag就破功了
      if(Math.abs(left-right) > 1) {
          flag = false
          // 后面再发生什么已经不重要了，返回一个不影响回溯计算的值
          return 0
      }
      // 返回当前子树的高度
      return Math.max(left, right) + 1
  }
  
  // 递归入口
  dfs(root) 
  // 返回flag的值
  return flag
};

完全二叉树

完全二叉树可以是这样的

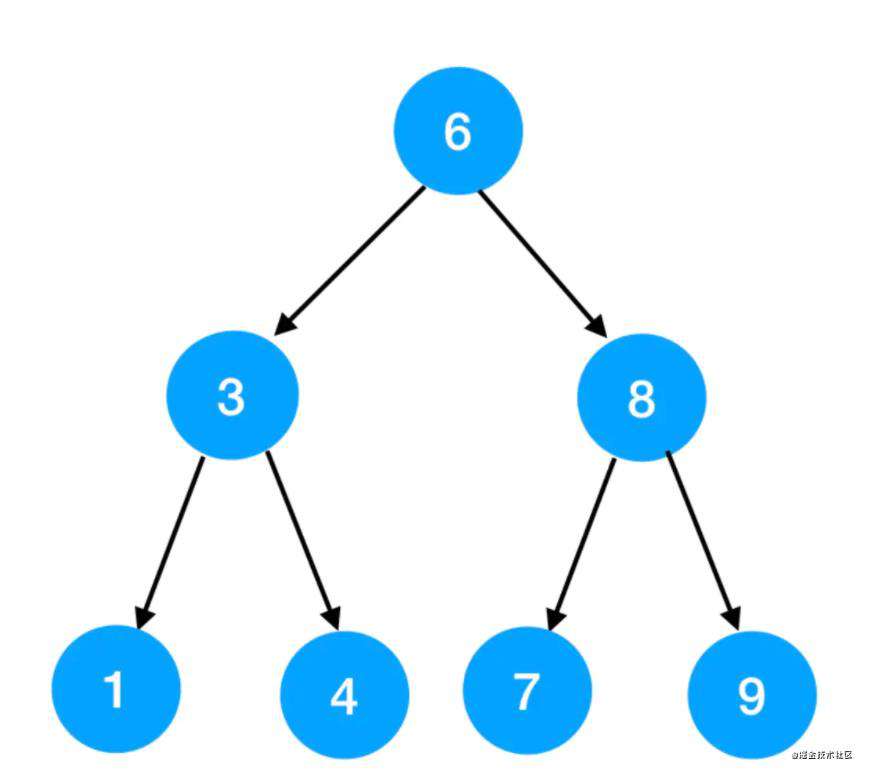
也可以是这样的

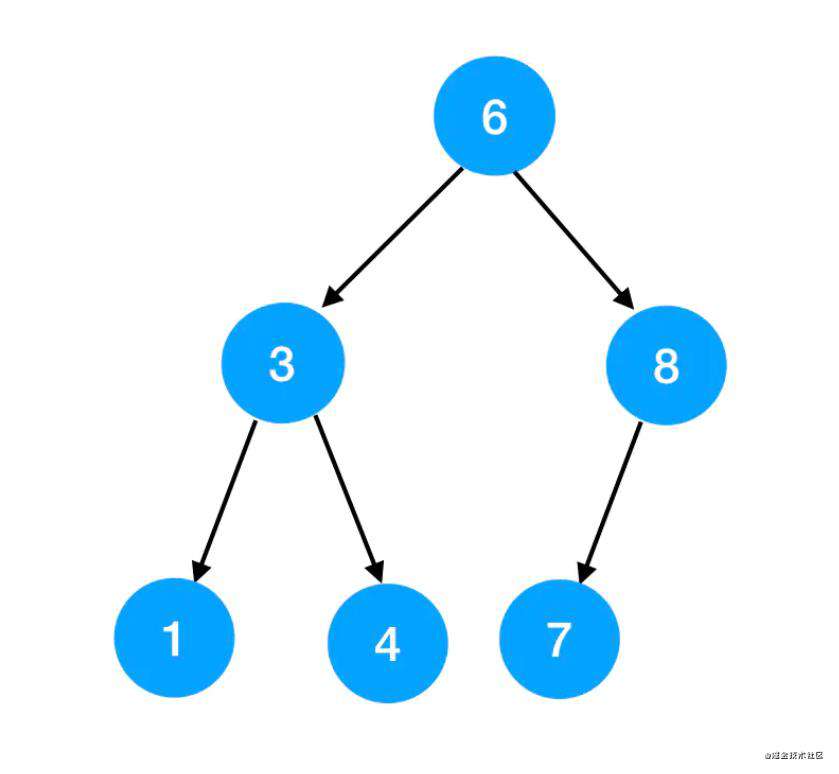
但不能是这样的

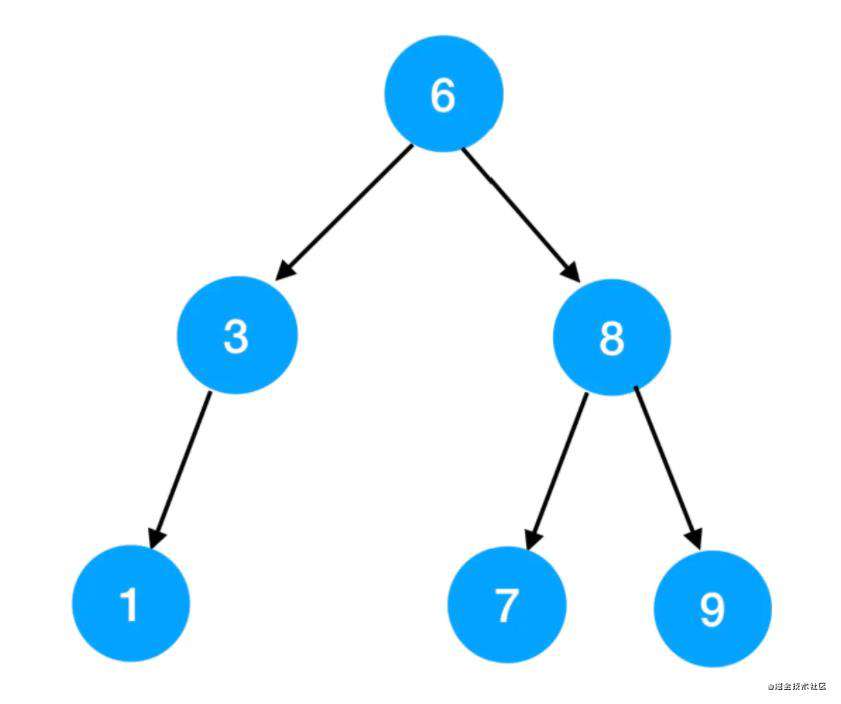
更不能是这样的

完全二叉树中有着这样的索引规律：假如我们从左到右、从上到下依次对完全二叉树中的结点从0开始进行编码（类似层序遍历的顺序）

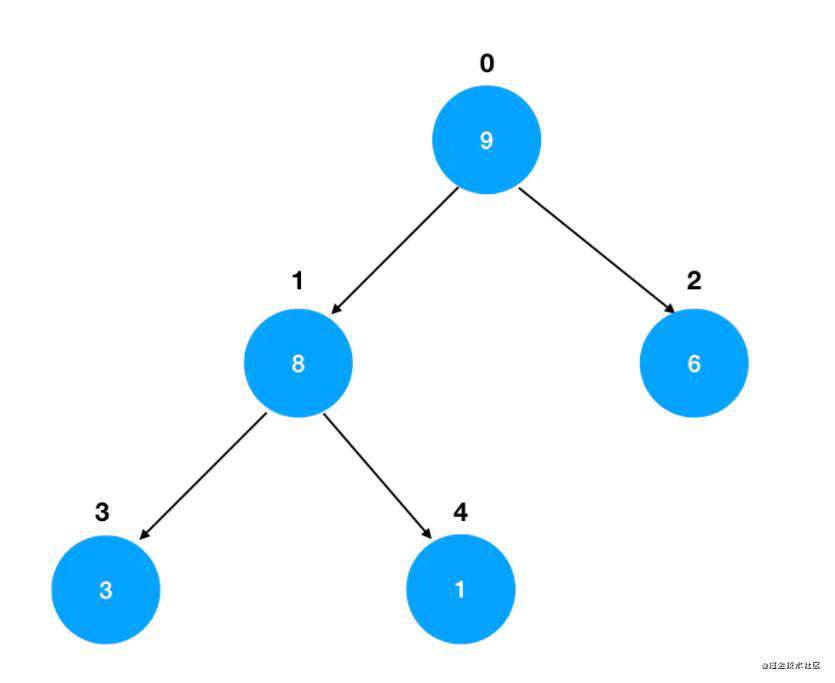
那么对于索引为 n 的结点来说：

• 索引为 (n-1)/2 的结点是它的父结点
• 索引 2*n+1 的结点是它的左孩子结点
• 索为引 2*n+2 的结点是它的右孩子结点

堆

堆是一种特殊的完全二叉树，根据特性不同，堆可以分为大顶堆和小顶堆。

大顶堆

如果一颗完全二叉树，其每个节点的值均不小于其左右节点的值，这样的完全二叉树就叫大顶堆

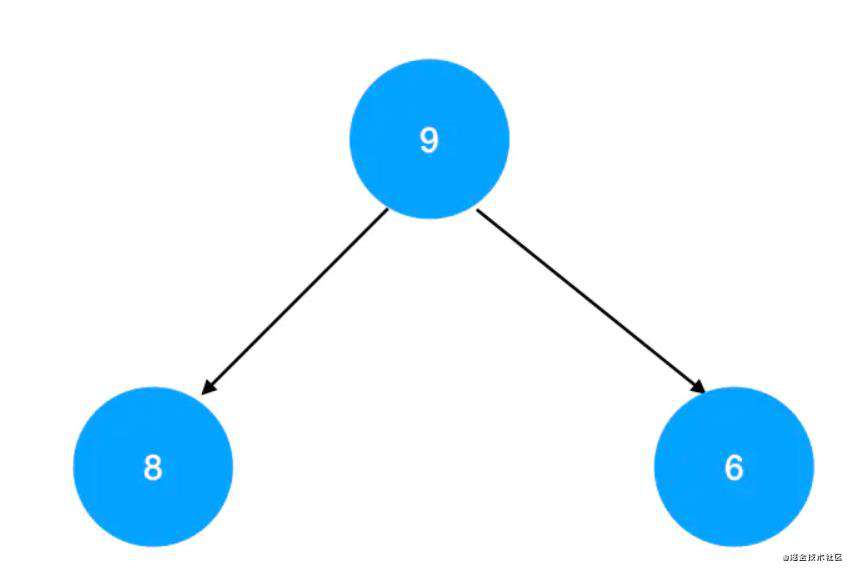
小顶堆

若一颗完全二叉树，树的每个节点的值均不大于其左右节点的值，这样的完全二叉树就叫小顶堆

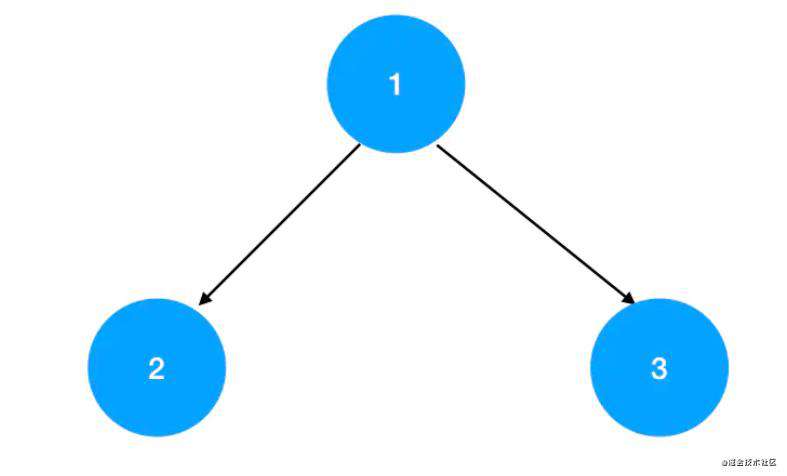
二叉树算法真题

翻转二叉树

输入

     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出

     4
   /   \
  7     2
 / \   / \
9   6 3   1

思路分析：翻转二叉树，即将每一颗子树的左右节点交换，最后得出垂直翻转的二叉树。既然是交换每一颗子树，意味着这个过程是重复的，可以考虑递归。所以本题的解题思路是，以递归的方式，遍历每个节点，并交换其左右子树。

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const invertTree = function(root) {
    // 定义递归边界
    if(!root) {
        return root;
    }
    // 递归交换右孩子的子结点
    let right = invertTree(root.right);
    // 递归交换左孩子的子结点
    let left = invertTree(root.left);
    // 交换当前遍历到的两个左右孩子结点
    root.left = right;
    root.right = left;
    return root;
};

以上，本文完！