一棵树-可视化之图形化基础之向量

可视化是前端可视化
图形是计算机图形学
向量就是那个向量，高中学过的，你懂的
树是那棵贼丑的树

结果

首先先看看本文最终的结果。一棵树-可视化之图形化基础之向量

是不是贼丑！是不是能在画展上卖个好价格！

过程

好了，话不多说，看看这棵贼丑的树是怎么诞生的吧。

坐标系

坐标系，或者说平面直角坐标系，是几何图形学的基础，其次是点、线、面这些元素。

坐标系大家都很熟悉，最初接触坐标系应该是初中，那时候的坐标系不知大家还有没有印象。

原点在中间，水平轴是 x 轴，竖轴是 y 轴，分为四个象限。

但是呢, html canvas 这货，默认原点在左上角， x 轴是跟平面直角坐标系是一致的， y 轴是向下的！！相信这种坐标轴在日常工作中使用 canvas 绘图给前端人不知道造成过多少麻烦，计算起来费事费力，还容易出 bug。

那么如何把 canvas 的坐标系变成平面直角坐标系呢

const canvas = document.querySelector('canvas')
const ctx = canvas.getContext('2d')
// 我们这里把原点定位在canvas左下角
ctx.translate(0, canvas.height)
// 关键步骤： 将canvasY轴方向翻转
ctx.scale(1, -1)

两行代码，就完成了对坐标系的翻转。

我们用一个 ? 来验证一下

假设，我们要在宽 512 * 高 256 的一个 Canvas 画布上实现如下的视觉效果。其中，山的高度是 100，底边 200，两座山的中心位置到中线的距离都是 80，太阳的圆心高度是 150。

我们这里使用 rough.js 增加一下趣味性

<canvas
  width="512"
  height="256"
  style="display: block;margin: 0 auto;background-color: #ccc"
></canvas>

const canvas = document.querySelector('canvas')
const rc = rough.canvas(canvas)
rc.ctx.translate(0, canvas.height)
rc.ctx.scale(1, -1)

const cSun = [canvas.width / 2, 106]
const diameter = 100 // 直径

const hill1Points = {
  start: [76, 0], // 起始点
  top: [176, 100], // 顶点
  end: [276, 0] // 终点
}

const hill2Points = {
  start: [236, 0], // 起始点
  top: [336, 100], // 顶点
  end: [436, 0] // 终点
}

const hill1Options = {
  roughness: 0.8,
  stokeWidth: 2,
  fill: 'pink'
}

const hill2Options = {
  roughness: 0.8,
  stokeWidth: 2,
  fill: 'chocolate'
}

function createHillPath(point) {
  const { start, top, end } = point

  return `M${start[0]} ${start[1]}L${top[0]} ${top[1]}L${end[0]} ${end[1]}`
}

function paint() {
  rc.path(createHillPath(hill1Points), hill1Options)
  rc.path(createHillPath(hill2Points), hill2Options)

  rc.circle(cSun[0], cSun[1], diameter, {
    stroke: 'red',
    strokeWidth: 4,
    fill: 'rgba(255, 255, 0, 0.4)',
    fillStyle: 'solid'
  })
}

paint()

这里我们翻转了坐标系，定义了 mountain1，mountain2，太阳的各个点的坐标，完全是参照直角坐标系的坐标。

最终的实现效果如下

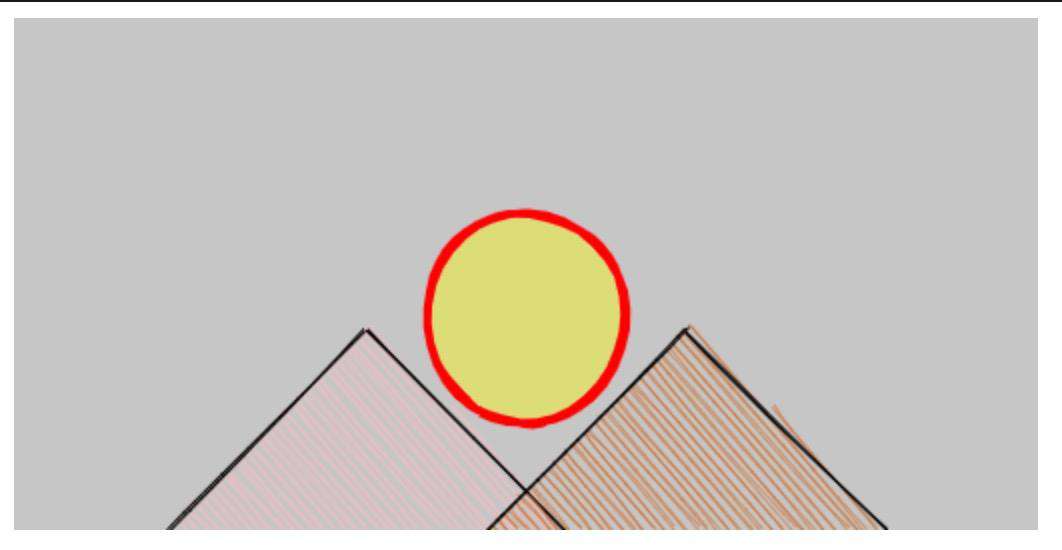
一棵树-可视化之图形化基础之向量

（是不是也能在画展上卖个不错的价格）

向量

定义

说完直角坐标系的转换，我们来讨论今天的正主， 向量（Vector）

向量的普遍定义是具有大小和方向的量，我们这里讨论的向量是几何向量，是用一组平面直角坐标系的坐标表示的例如 (1, 1), 意思是，顶点坐标为 x 为 1，y 为 0 的一条有向线段，向量的方向是由原点(0, 0) 指向顶点(1,1)的方向。

换言之，知道了向量的顶点，就知道了向量的大小和方向

向量的模

向量的大小也叫向量的模，是向量坐标的平方和的算术平方根， length = Math.pow((x**2 + y**2), 0.5)。

向量的方向

向量的方向一方面可以使用向量的顶点表示。

另外一方面使用向量和 x 轴的夹角，也能够表示一个向量。

使用 javascript Math 的内置方法可以得到，计算方式：

// 构造函数在本文稍后的地方介绍
const v = new Vector2D(1, 10)
const dir = Math.atan2(v.y, v.x)

四则运算

加减法

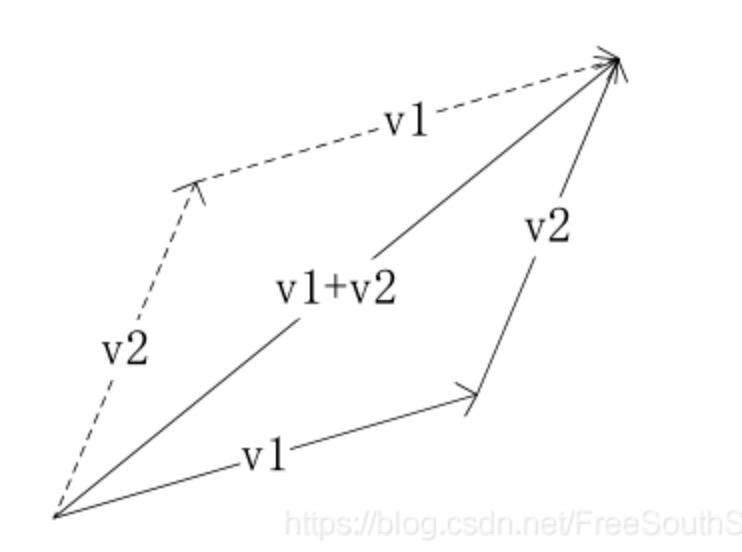
示意图: 一棵树-可视化之图形化基础之向量

如图所示：向量 v1(x1, y1)和向量 v2(x2, y2)相加得到的新的向量就是两个向量对应坐标之和, 用公式表达就是 v1(x1, y1) + v2(x2, y2) = v3(x1 + x2, y1 + y2)

反之就是减法 v3(x1 + x2, y1 + y2) - v2 (x2, y2)= v1(x1, y1)

乘除

向量乘法有叉乘和点乘

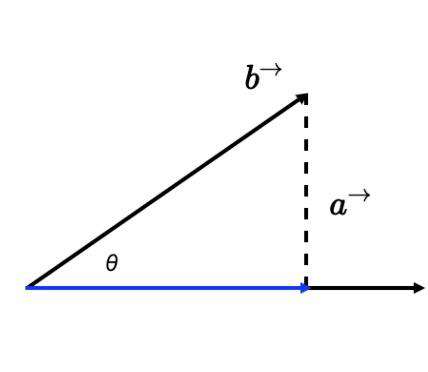
一棵树-可视化之图形化基础之向量

物理意义是，方向为 va 方向，大小为 va.length 的力，沿 vb 方向拉动 vb.length 距离所做的功

va * vb = va.length * vb.length * cos(rad)

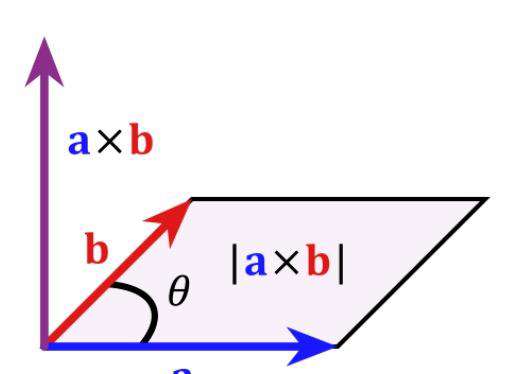
一棵树-可视化之图形化基础之向量

va * vb = va.length * va.length * sin(rad)

也可以理解为长度为 va.length 的线段沿着 vb 方向移动到 vb 顶点扫过的面积，反之就是除法

单位向量

长度为 1 的向量叫做单位向量，满足这个条件的向量有无数条，一个非 0 的向量除以他的模，就是这个向量的单位向量，我们取与 x 轴夹角为 0 的向量：**[1, 0]**作为单位向量

向量的旋转

将一个向量转动一定的角度 rad 之后的向量该如何计算呢。这里有比较复杂的推导过程，因此可以直接记住结论。

具体代码在下面构造函数里面展示

构造器

// 用一个长度为2的数组表示一个向量， 下标为0的位置表示x 下标为1的位置表示 y
class Vector2D extends Array {
  constructor(x = 1, y = 0) {
    super(x, y)
  }

  get x() {
    return this[0]
  }

  get y() {
    return this[1]
  }

  set x(v) {
    this[0] = v
  }

  set y(v) {
    this[1] = v
  }

  add(v) {
    this.x = this.x + v.x
    this.y = this.y + v.y
    return this
  }

  length() {
    return Math.hypot(this.x, this.y)
  }

  rotate(rad) {
    const c = Math.cos(rad)
    const s = Math.sin(rad)
    const [x, y] = this
    this.x = x * c + y * -s
    this.y = x * s + y * c
    return this
  }
}

至此，画出文章开头的那个图形的基本要素都已经准备好了。下面，让我们来见证一下世界名画的产生。

动手画图

准备一个 512 * 512 的画布

<html>
  ...
  <canvas
    width="512"
    height="512"
    style="display:block;margin:0 auto;background-color: #ccc"
  ></canvas>
  ...
</html>

翻转 canvas 坐标系

const canvas = document.querySelector('canvas')
const ctx = canvas.getContext('2d')
ctx.translate(0, canvas.height)
ctx.scale(1, -1)

定义绘制树枝的方法

/**
 * 1. ctx canvas ctx 上下文对象
 * 2. 起始向量
 * 3. length 向量长度(树枝长度)
 * 4. thickness 线段宽度
 * 5. 单位向量 dir 旋转角度
 * 6. bias 随机因子
 */
const canvas = document.querySelector('canvas')
const ctx = canvas.getContext('2d')
ctx.translate(0, canvas.height)
ctx.scale(1, -1)
ctx.lineCap = 'round'
console.log(canvas.width)
const v0 = new Vector2D(canvas.width / 2, 0)

function drawBranch(ctx, v0, length, thickness, rad, bias) {
  const v = new Vector2D().rotate(rad).scale(length)
  console.log(v, rad, length)
  const v1 = v0.copy().add(v)
  ctx.beginPath()
  ctx.lineWidth = thickness
  ctx.moveTo(...v0)
  ctx.lineTo(...v1)
  ctx.stroke()
  ctx.closePath()
}
// 定义好了之后我们先画一个树枝试试看
drawBranch(ctx, v0, 50, 10, Math.PI / 2, 1)

递归画图

// 先定义收缩系数
const LENGTH_SHRINK = 0.9
const THICKNESS_SHRINK = 0.8
const RAD_SHRINK = 0.5
const BIAS_SHRINK = 1

function drawBranch(ctx, v0, length, thickness, rad, bias) {
  //....

  if (thickness > 2) {
    // 画左树枝
    const left =
      Math.PI / 4 +
      RAD_SHRINK * (rad + 0.2) +
      drawBranch(
        ctx,
        v1,
        length * LENGTH_SHRINK,
        thickness * THICKNESS_SHRINK,
        left,
        bias
      )

    // 画右树枝
    const right = Math.PI / 4 + RAD_SHRINK * (rad - 0.2)
    drawBranch(
      ctx,
      v1,
      length * LENGTH_SHRINK,
      thickness * THICKNESS_SHRINK,
      right,
      bias
    )
  }
}
drawBranch(ctx, v0, 50, 10, Math.PI / 2, 1)

这一步画出来的是一个比较规则的形状，代码写到这一步，树的基本形状已经出来了，但是为了展示效果，向量翻转上加一些随机性来画一颗更加接近自然状态的树。代码如下：

function drawBranch(ctx, v0, length, thickness, rad, bias) {
  // ...

  if (thickness > 2) {
    // 画左树枝
    const left =
      Math.PI / 4 + RAD_SHRINK * (rad + 0.2) + bias * (Math.random() - 0.5)
    drawBranch(
      ctx,
      v1,
      length * LENGTH_SHRINK,
      thickness * THICKNESS_SHRINK,
      left,
      bias
    )

    // 画右树枝
    const right =
      Math.PI / 4 + RAD_SHRINK * (rad - 0.2) + bias * (Math.random() - 0.5)
    drawBranch(
      ctx,
      v1,
      length * LENGTH_SHRINK,
      thickness * THICKNESS_SHRINK,
      right,
      bias
    )
  }
}
drawBranch(ctx, v0, 50, 10, Math.PI / 2, 1)

等等等等，效果图：一棵光秃秃的树

效果图：一棵树-可视化之图形化基础之向量（是不是有点艺术内味儿了）

剩下的就是添加一些点缀，把果子挂上

function drawBranch(ctx, v0, length, thickness, rad, bias) {
  // ...

  if (thickness < 5 && Math.random() < 0.3) {
    const th = 6 + Math.random()

    ctx.save()
    ctx.strokeStyle = '#e4393c'
    ctx.lineWidth = th
    ctx.beginPath()
    ctx.moveTo(...v1)
    ctx.lineTo(v1.x, v1.y + 2)
    ctx.stroke()
    ctx.closePath()
    ctx.restore()
  }
}

// 这里增大了随机因子， 让树枝更加分散
drawBranch(ctx, v0, 50, 10, Math.PI / 2, 1)

此时效果图就出来了：一棵树-可视化之图形化基础之向量

总结

本文首先展示了如何将 canvas 的坐标系转化为直角坐标系

其次用一个例子演示了，向量在图形学内的基本运算。

向量运算的意义并不仅仅只是用来算点的位置和构造线段，这只是最初级的用法。

可视化呈现依赖于计算机图形学，而向量运算是整个计算机图形学的数学基础。而且，在向量运算中，除了加法表示移动点和绘制线段外，向量的点乘、叉乘运算也有特殊的意义。

一棵树-可视化之图形化基础之向量

结果

过程

坐标系

向量

定义

向量的模

向量的方向

四则运算

加减法

乘除

单位向量

向量的旋转

构造器

动手画图

总结

常见问题FAQ

掘金(wuyanzu666) SVIP

发表评论

如需帝国cms功能定制以及二次开发请联系我们

升级SVIP会员

工作时间

结果

过程

坐标系

向量

定义

向量的模

向量的方向

四则运算

加减法

乘除

单位向量

向量的旋转

构造器

动手画图

总结

常见问题FAQ

掘金(wuyanzu666) SVIP

相关推荐

发表评论

如需帝国cms功能定制以及二次开发请联系我们

升级SVIP会员

工作时间

请选择支付方式