这是我参与8月更文挑战的第26天,活动详情查看:8月更文挑战。
前言
今天我们聊聊我们经常用的CSS3动画里面的贝尔赛曲线,希望能做到,她认识你,你也熟悉她! 本文源码: Bezier
看完你就懂了一半,动手你就成功了另外一半!
贝塞尔曲线在前端
css3的动画主要是
- transition
- animation
transition有transition-timing-function
animation有animation-timing-function
以transition-timing-function为例
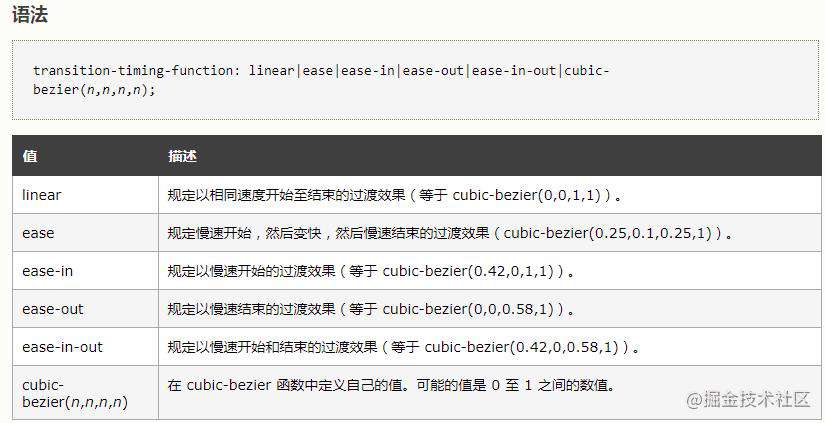
其内置 ease,linear,ease-in,ease-out,ease-in-out,就是贝塞尔曲线函数, 作用是控制属性变化的速度。
也可以自定义cubic-bizier(x1,y1,x2,y2), 这个嘛玩意呢,三阶贝塞尔曲线, x1,y1与 x2,y2是两个控制点。
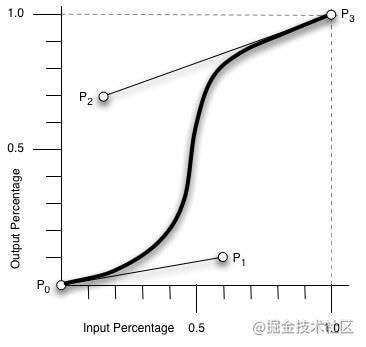
如图:
x1, y1对应 P1点, x2,y2 对应P2点。
要点:
- 曲线越陡峭,速度越快,反之,速度越慢!
- 控制点的位置会影响曲线形状
说道这里, 回想一下我们前端在哪些地方还会贝塞尔呢。
svgcanvas/webglcss3动画animation Web API
千万别以为JS就不能操作CSS3动画了
这样说可能有些空洞,我们一起来看看曲线和实际的动画效果:
红色ease和ease-out曲线前期比较陡峭,加速度明显比较快。
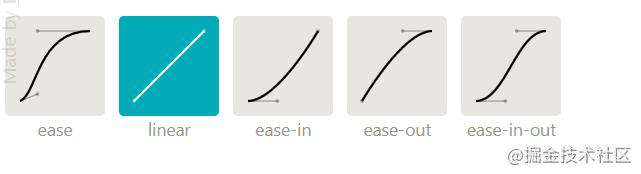
贝塞尔曲线运动-演示地址

什么是贝赛尔曲线
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。
公式怎么理解呢?这里你可以假定
- P0的坐标(0,0), 最终的点的坐标为(1,1)
t从0不断的增长到1
把t的值和控制点的x坐标套入公式,得到一个新的x坐标值
把t的值和控制点的y坐标套入公式,得到一个新的y坐标值
(新的x坐标值 , 新的y坐标值)坐标就是t时刻曲线的点的坐标。
通用公式
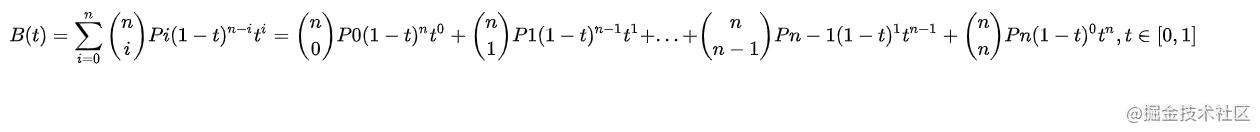
线性公式
无控制点,直线
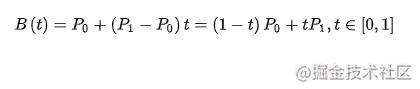
二次方公式
一个控制点
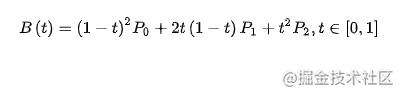
三次方公式
两个控制点
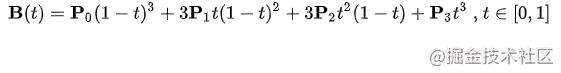
这是我们的重点,因为css动画都是三次方程式
P0作为起点,P3作为终点, 控制点是P1与P2, 因为我们一般会假定 P0 为 (0,0), 而 P3为(1,1)。
控制点的变化,会影响整个曲线,我们一起来简单封装一下并进行实例操作。
一阶二阶三阶封装
我们基于上面公式的进行简单的封装,
你传入需要的点数量和相应的控制点就能获得相应一组点的信息。
class Bezier {
getPoints(count = 100, ...points) {
const len = points.length;
if (len < 2 || len > 4) {
throw new Error("参数points的长度应该大于等于2小于5");
}
const fn =
len === 2
? this.firstOrder
: len === 3
? this.secondOrder
: this.thirdOrder;
const retPoints = [];
for (let i = 0; i < count; i++) {
retPoints.push(fn.call(null, i / count, ...points));
}
return retPoints;
}
firstOrder(t, p0, p1) {
const { x: x0, y: y0 } = p0;
const { x: x1, y: y1 } = p1;
const x = (x1 - x0) * t;
const y = (y1 - y0) * t;
return { x, y };
}
secondOrder(t, p0, p1, p2) {
const { x: x0, y: y0 } = p0;
const { x: x1, y: y1 } = p1;
const { x: x2, x: y2 } = p2;
const x = (1 - t) * (1 - t) * x0 + 2 * t * (1 - t) * x1 + t * t * x2;
const y = (1 - t) * (1 - t) * y0 + 2 * t * (1 - t) * y1 + t * t * y2;
return { x, y };
}
thirdOrder(t, p0, p1, p2, p3) {
const { x: x0, y: y0 } = p0;
const { x: x1, y: y1 } = p1;
const { x: x2, y: y2 } = p2;
const { x: x3, y: y3 } = p3;
let x =
x0 * Math.pow(1 - t, 3) +
3 * x1 * t * (1 - t) * (1 - t) +
3 * x2 * t * t * (1 - t) +
x3 * t * t * t;
let y =
y0 * (1 - t) * (1 - t) * (1 - t) +
3 * y1 * t * (1 - t) * (1 - t) +
3 * y2 * t * t * (1 - t) +
y3 * t * t * t;
return { x, y };
}
}
export default new Bezier();
可能,你觉得太空洞,那么我们看一下demo和截图。
演示地址: xiangwenhu.github.io/juejinBlogs…
一阶贝塞尔是一条直线:
二阶贝塞尔一个控制点:

三阶贝塞尔两个控制点:
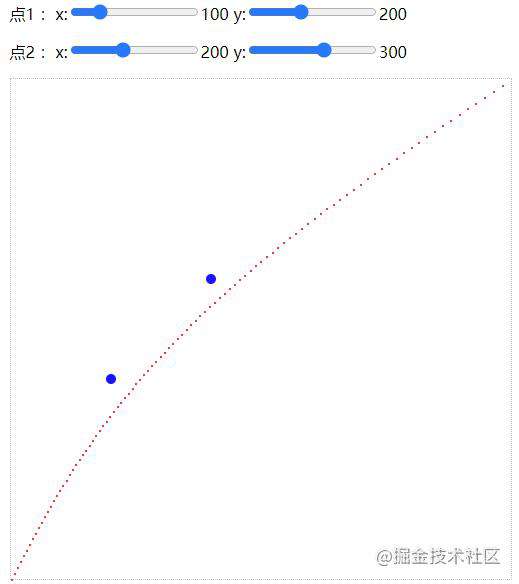
贝塞尔曲线控制点
回到最开始, animation和 transition都可以自定义三阶贝塞尔函数, 而需要的就是两个控制点的信息,怎么通过测试曲线获得控制点呢?
在线取三阶贝塞尔关键的方案早就有了。
但是不妨碍我自己去实现一个简单,加强理解。
大致的实现思路
- canvas 绘制效果
canvas有bezierCurveTo方法,直接可以绘制贝塞尔曲线 - 两个控制点用dom元素来显示
逻辑
- 点击时计算最近的点,同时修改最近点的坐标
- 重绘
当然这只是一个简单的版本。
演示地址: xiangwenhu.github.io/juejinBlogs…
截图: 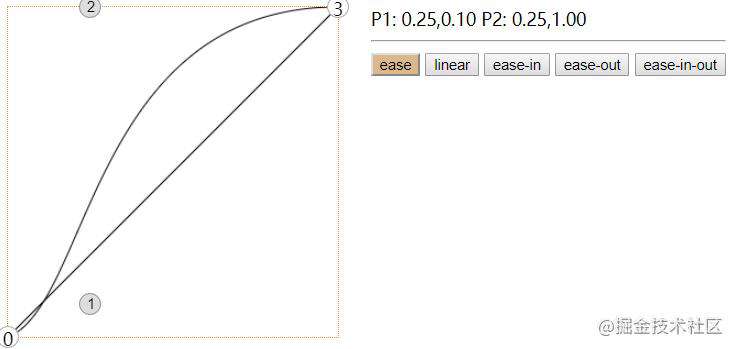
有了这个,你就可以通过曲线获得控制点了, 之前提到过,曲线的陡峭决定了速度的快慢,是不是很有用呢?
当然,你可以自己加个贝塞尔的直线运动,查看实际的运动效果,其实都不难,难的是你不肯动手!!!
写在最后
如果你觉得不错,你的一赞一评就是我前行的最大动力。
技术交流群请到 这里来。 或者添加我的微信 dirge-cloud,一起学习。
参考引用
贝塞尔曲线扫盲
在线贝塞尔
在线贝塞尔2
可视化n次贝塞尔曲线及过程动画演示--大宝剑
贝塞尔曲线算法,js贝塞尔曲线路径点
贝塞尔曲线算法之JS获取点
github.com/mtsee/Bezie…
n 阶贝塞尔曲线计算公式实现
前端贝塞尔曲线效果汇总
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?




发表评论
还没有评论,快来抢沙发吧!