
一、背景
工作和生活中我们会经常碰到矩形树图,下面两张图相信大家不会陌生。
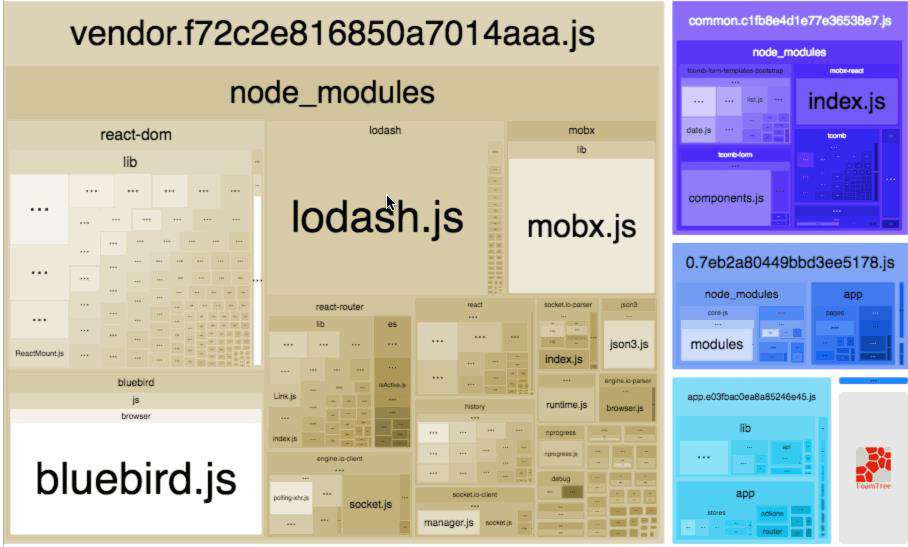
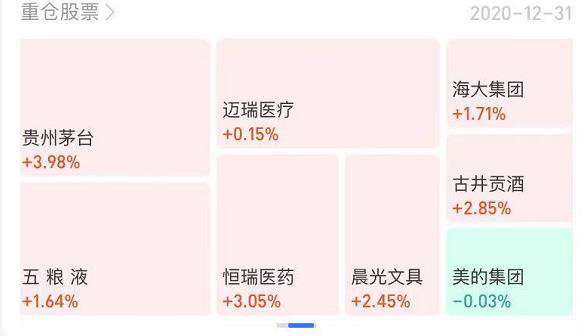
最近刚好接到一个需求,绘制门诊疾病的矩形树图(如下图),虽然 echart, d3等框架都有相关的实现,但是对其实现还是蛮好奇的,遂深入研究了一下其实现原理。接下来会从布局算法,颜色填充和canvas 事件系统三个方面介绍矩形树图的实现。
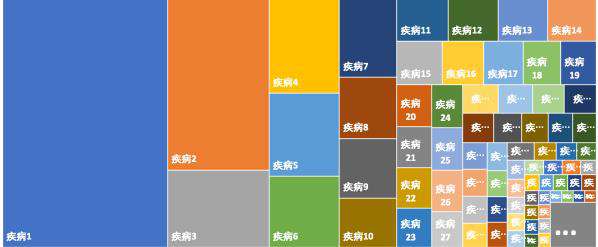
二、布局算法
我们假设有一组排好序的数据,为方便value之和为100
const data = [
{
name: '疾病1',
value: 36,
},
{
name: '疾病2',
value: 30,
},
{
name: '疾病3',
value: 23,
},
{
name: '疾病4',
value: 8,
},
{
name: '疾病5',
value: 2,
},
{
name: '疾病6',
value: 1,
}
]
2.1 Slice and Dice 算法 - 从最简单的实现开始
需求中矩形树图最容易识别特征就是 小矩形的面积/总面积 = 该疾病患者数/患者总数,如果只按照这个特征来实现的话即自左至右的对矩形进行填充,填充时仅考虑小矩形的面积,效果如下图

我们发现不论是美观度,还是区分度都不理想,占比较小的最右侧矩形没有存在感,鼠标很不容易选中以查看详细信息。
2.2 Squarified 算法 - 正方形化
接下来我们进一步提取需求特征来优化布局。我们发现需求中并没有狭长的矩形,而是大部分矩形都非常接近正方形,实际上平均长宽比是评价矩形树图的第一指标。Bruls 于1999年提出了名为 Squarified 的布局算法:
- 将子节点按照权重(这里是value)进行降序排列
- 从第一个子节点开始,按照沿最短边,紧靠左边或上边(取决于最短边)的原则,分别采用自左至右或自上而下的填充策略填充到大矩形中
- 当插到第 i 个子节点矩形时,分别计算采用同行同列和新建一行/列两种模式,对比第1至第i-1个已填充小矩形的平均长宽比,选择平均长宽比低(靠近1)的作为第i个节点的填充方式
不难发现,这其实是一个递归的过程,带有注释的核心代码如下:
/**
* @param {Array} children 待layout的矩形面积数组
* @param {Array} row 正要layout的矩形面积数组
* @param {Number} minSide 短边
*/
const squarify = (children, row, minSide) => {
// 递归出口
if (children.length === 1) {
return layoutLastRow(row, children, minSide);
}
const rowWithChild = [...row, children[0]];
// 当正在layout的矩形数组row为空
// 或者 加上children[0]的rowWithChild最差长宽比 相比于row 更好(接近1)
// 这里可能会有点难理解,其实此处的逻辑对应上面描述的第三步。
// 满足此条件,采用同行同列(到底是同行还是同列,取决于短边是哪个)方式填充,否则新建一行/一列
if (row.length === 0 || worstRatio(row, minSide) >= worstRatio(rowWithChild, minSide)) {
// 将children[0]从children删除
children.shift();
// 递归执行 squarify
return squarify(children, rowWithChild, minSide);
} else {
// 将 row 内的小矩形绘制出来
layoutRow(row, minSide, getMinSide().vertical);
return squarify(children, [], getMinSide().value);
}
};
/**
* 最差长宽比(公式见参考1,此处不再推理)
* @param {Array} row
* @param {Number} minSide 短边
*/
function worstRatio(row, minSide) {
const sum = row.reduce(sumReducer, 0);
const rowMax = getMaximum(row);
const rowMin = getMinimum(row);
return Math.max(((minSide ** 2) * rowMax) / (sum ** 2), (sum ** 2) / ((minSide ** 2) * rowMin));
}
const Rectangle = {
data: [],
xBeginning: 0,
yBeginning: 0,
totalWidth: canvasWidth,
totalHeight: canvasHeight,
};
/**
* 获取最短边,若高为短边,则垂直,否则水平
*/
const getMinSide = () => {
if (Rectangle.totalHeight > Rectangle.totalWidth) {
return { value: Rectangle.totalWidth, vertical: false };
}
return { value: Rectangle.totalHeight, vertical: true };
};
/**
* 计算在要layout的row中每个矩形的坐标(x,y,width,height)
* 为方便理解,这里仅展示vertical为true的代码,即短边为高
* @param {Array} row
* @param {Number} height 短边
* @param {Boolean} vertical 是否垂直布局
*/
const layoutRow = (row, height, vertical) => {
// 先算总面积,除以高(短边),可得宽
// 因小矩形是沿着高填充的,则所有row中小矩形的高之和等于Rectangle中的高,小矩形宽为rowWidth
// 什么叫做沿高填充见下注释图,小矩形A和小矩形B为沿高填充
// _______________________________
// | A | |
// |____________| |
// |_____B______|__________________|
// {--rowWidth--}
const rowWidth = row.reduce(sumReducer, 0) / height;
row.forEach((rowItem) => {
const rowHeight = rowItem / rowWidth; // 小矩形的高
const { xBeginning } = Rectangle;
const { yBeginning } = Rectangle;
let data;
if (!vertical) {
// 小矩形的位置信息,
data = {
x: xBeginning,
y: yBeginning,
width: rowWidth,
height: rowHeight,
};
// 移动 yBeginning,以绘制下一个小矩形
Rectangle.yBeginning += rowHeight;
}
Rectangle.data.push(data);
});
// row 内的小矩形绘制完成后
// 重置xBeginning,yBeginning,totalWidth 的值
if (vertical) {
Rectangle.xBeginning += rowWidth;
Rectangle.yBeginning -= height;
Rectangle.totalWidth -= rowWidth;
}
};
其绘图过程如图所示
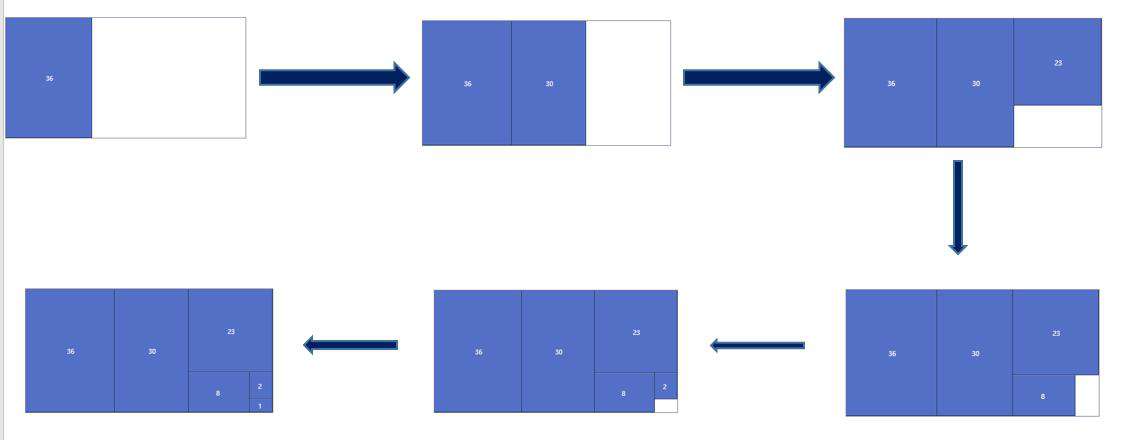
2.3 其它算法
Pivot算法和Strip算法: Squarified 算法极大地改善了矩形的长宽比,但是在绘制图形时对数据集先进行了排序。当权值发生改变时,新旧树图之间会有很大的跳变,其稳定性较差。Pivot算法和Strip算法平衡了长宽比和稳定性。BinaryTree二叉树来布局算法:递归地将指定节点划分为近似平衡的二叉树,为宽矩形选择水平分区,为高矩形选择垂直分区的布局方式
本文不再详细探讨细节,有兴趣见参考链接第二条。
2.4 评价指标
我们主要从平均长宽比 AAR,稳定性,连续性等指标评价树图布局算法的性能。
三、颜色填充
这个过程比较简单,参考 Echart 的方案,可以设置一个固定的颜色数组,循环取用
const colors = ['#c23531', '#2f4554', '#61a0a8', '#d48265', '#91c7ae', '#749f83', '#ca8622']
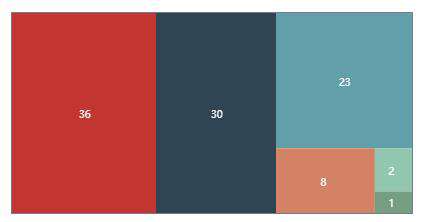
四、Canvas 事件系统
当鼠标移动到某个小矩形上时,我们希望可以展示tips。由于 Canvas 是作为一个整体画布存在,所有的内容只不过是其内部渲染的结果,我们不能像在 Dom 元素上监听事件一样,在 Canvas 所渲染的图形内绑定各种事件。那各个小矩形如何监听鼠标事件?
- 我们可以通过下面两个API来模拟实现给小矩形添加事件(Path2D存在兼容问题)
isPointInPath(path, x, y, fillRule)用于检测(x, y)是否在path上- path:Path2D应用的路径。
- x:检测点的X坐标
- y:检测点的Y坐标
- fillRule: 用来决定点在路径内还是在路径外的算法。"nonzero": 非零环绕规则 ,默认的规则。"evenodd": 奇偶环绕原则 。
Path2D:声明路径,具有与 ctx 相同的路径方法(比如beginPath,moveTo等)
精简后的核心代码如下:
interface diseaseInfo {
name: string;
value: number;
}
interface rectInfo {
x: number;
y: number;
width: number;
height: number;
data: diseaseInfo
}
rects.forEach((item: rectInfo) => {
const path = new Path2D()
path.rect(item.x, item.y, item.width, item.height)
ctx.fill(path)
item.path = path
})
const canvasInfo = canvas.getBoundingClientRect()
canvas.addEventListener('mousemove', (e) => {
result.forEach(item => {
if(ctx.isPointInPath(item.path, e.clientX - canvasInfo.left, e.clientY - canvasInfo.top)) {
// 展示tips
showTips(e.clientX, e.clientY, item.data)
}
})
})
-
在社区中还看到一种思路,很是巧妙。其核心原理是镜像出一个离屏Canvas
OffscreenCanvas,在绘制子元素的时候随机一个子元素id,且对应唯一一个rgba色值,然后将子元素以此色值同步绘制到OffscreenCanvas上,(原canvas与OffscreenCanvas的唯一区别是各个小矩形的像素值不同,位置大小完全一样)。当原canvas上监听到鼠标事件时,可获取相对坐标(x,y),再结合getImageDataAPI(返回值包含(x,y)的rgba值) 在OffscreenCanvas找到坐标(x,y)对应的色值,进而找到子元素id -
其它
- 射线法(判断点与多边形一侧的交点个数为奇数,则点在多边形内部。)
- 角度法(如果一个点在多边形内部,则该点与多边形所有顶点两两构成的夹角,相加应该刚好等于360°。仅适用凸多边形)
一般成熟的可视化框架都有一套基于发布订阅模式的事件系统来支撑在Canvas内绑定各种事件。
经过一系列的操作最终实现效果如下:
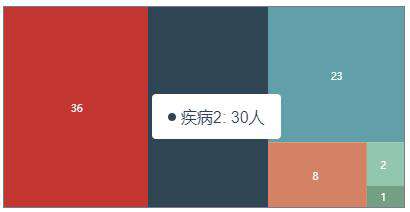
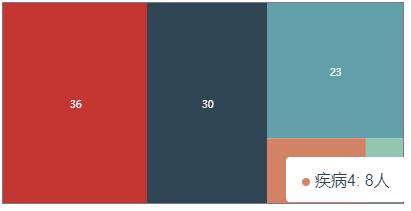
五、参考资料
- www.win.tue.nl/~vanwijk/st…
- zhuanlan.zhihu.com/p/57873460
- juejin.cn/post/688820…

常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!