前言

在最近的项目中，会设计到金额单位的变化，比如分和元之间的互相转换。

但是偶然中在计算4.35 * 100时，返回的结果并不是预期的435，而是434.99999999999994。意识到，可能遇见JavaScript中的经典问--0.1 + 0.2是否等于0.3了。

原因分析

0.1转二进制是无限循环的

我们知道在计算机中数据都是以二进制来保存的，而将10进制的小数转为二进制数据，采用乘2取整，顺序排列。

比如，例如把0.8125转换为二进制小数：

那么，根据上面的内容，我们将0.1转换为二进制小数的步骤如下：

0.1 * 2 = 0.2
0.2 * 2 = 0.4 // 注意这里
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4 // 注意这里，循环开始
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
...

可以看到，由于最后一位不是以5结尾（仅0.5 * 2才能得出整数），所以最后得到的二进制数据是一个无限二进制小数0.00011001100...。

Javascript的精度

在Javascript中整数和小数都遵循IEEE 754标准（即标准的double双精度浮点数），使用64位固定长度来表示。

在该规则中，数据在计算机中保存结构如下：

• sign(符号): 占 1 bit, 表示正负;
• exponent(指数): 占 11 bit，表示范围;
• mantissa(尾数): 占 52 bit，表示精度，多出的末尾如果是 1 需要进位;

再根据下面的公式，我们计算出二进制数据V：

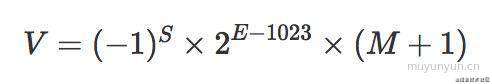
这里，我们以上面的0.1为例，对应二进制数据0.00011001100...，用科学计数法表示为1.100110011... x 2^(-4)，根据上述公式，S为0(1 bit)，E为-4 + 1023，对应的二进制为01111111011(11 bit)，M为1001100110011001100110011001100110011001100110011010。

这里我们可以看到，0.1的精度在JavaScript中丢失了。

同样的道理，0.2在JavaScript为0.0011001100110011001100110011001100110011001100110011010，也会存在精度丢失的情况。

那么，0.1+0.2得出二进制数据如下，结果转为10进制则为0.30000000000000004：

// 计算过程
0.00011001100110011001100110011001100110011001100110011010
0.0011001100110011001100110011001100110011001100110011010

// 相加得
0.01001100110011001100110011001100110011001100110011001110

解决方案

项目出现了问题，就得解决。通过和团队其他伙伴沟通，找到了一个第三方库number-precision，来解决这个问题。

import NP from 'number-precision'

NP.strip(0.09999999999999998); // = 0.1
NP.times(3, 0.3);              // 3 * 0.3 = 0.9, not 0.8999999999999999
NP.divide(1.21, 1.1);          // 1.21 / 1.1 = 1.1, not 1.0999999999999999
NP.plus(0.1, 0.2);             // 0.1 + 0.2 = 0.3, not 0.30000000000000004
NP.minus(1.0, 0.9);            // 1.0 - 0.9 = 0.1, not 0.09999999999999998

下面简单分析下源码。

NP.strip

/**
 * 把错误的数据转正
 * strip(0.09999999999999998)=0.1
 */
function strip(num: numType, precision = 15): number {
  return +parseFloat(Number(num).toPrecision(precision));
}

我们可以看到，这里使用了toPrecision方法。

以0.09999999999999998为例：

0.09999999999999998.toPrecision(15) // 输出字符串："0.100000000000000"

再通过parseFloat方法，将返回的字符串转换为对应的浮点数。

parseFloat(0.09999999999999998.toPrecision(15)) // 输出数字：0.1

NP.times

/**
 * 精确乘法
 */
function times(num1: numType, num2: numType, ...others: numType[]): number {
  if (others.length > 0) {
    return times(times(num1, num2), others[0], ...others.slice(1));
  }
  const num1Changed = float2Fixed(num1);
  const num2Changed = float2Fixed(num2);
  const baseNum = digitLength(num1) + digitLength(num2);
  const leftValue = num1Changed * num2Changed;

  checkBoundary(leftValue);

  return leftValue / Math.pow(10, baseNum);
}

该方法前半部分，通过递归用于实现两个以上参数相乘。我们主要看后半部分的逻辑。

这里先介绍几个前置函数：

/**
 * Return digits length of a number
 * @param {*number} num Input number
 */
function digitLength(num: numType): number {
  // Get digit length of e
  const eSplit = num.toString().split(/[eE]/);
  const len = (eSplit[0].split('.')[1] || '').length - +(eSplit[1] || 0);
  return len > 0 ? len : 0;
}

/**
 * 把小数转成整数，支持科学计数法。如果是小数则放大成整数
 * @param {*number} num 输入数
 */
function float2Fixed(num: numType): number {
  if (num.toString().indexOf('e') === -1) {
    return Number(num.toString().replace('.', ''));
  }
  const dLen = digitLength(num);
  return dLen > 0 ? strip(Number(num) * Math.pow(10, dLen)) : Number(num);
}

/**
 * 检测数字是否越界，如果越界给出提示
 * @param {*number} num 输入数
 */
function checkBoundary(num: number) {
  if (_boundaryCheckingState) {
    if (num > Number.MAX_SAFE_INTEGER || num < Number.MIN_SAFE_INTEGER) {
      console.warn(`${num} is beyond boundary when transfer to integer, the results may not be accurate`);
    }
  }
}

我们可以看出，乘法的逻辑就是先放大，再缩小。先将小数转换为整数，再进行相乘，最后再将结果按照所有相乘数据的小数之和进行缩小。

NP.divide

/**
 * 精确除法
 */
function divide(num1: numType, num2: numType, ...others: numType[]): number {
  if (others.length > 0) {
    return divide(divide(num1, num2), others[0], ...others.slice(1));
  }
  const num1Changed = float2Fixed(num1);
  const num2Changed = float2Fixed(num2);
  checkBoundary(num1Changed);
  checkBoundary(num2Changed);
  // fix: 类似 10 ** -4 为 0.00009999999999999999，strip 修正
  return times(num1Changed / num2Changed, strip(Math.pow(10, digitLength(num2) - digitLength(num1))));
}

除法在乘法的基础之上进行调整，将待操作数据转变为整数，先进行相除。再按照小数位的差值，进行放大&缩小。

NP.plus和NP.minus

/**
 * 精确加法
 */
function plus(num1: numType, num2: numType, ...others: numType[]): number {
  if (others.length > 0) {
    return plus(plus(num1, num2), others[0], ...others.slice(1));
  }
  const baseNum = Math.pow(10, Math.max(digitLength(num1), digitLength(num2)));
  return (times(num1, baseNum) + times(num2, baseNum)) / baseNum;
}

/**
 * 精确减法
 */
function minus(num1: numType, num2: numType, ...others: numType[]): number {
  if (others.length > 0) {
    return minus(minus(num1, num2), others[0], ...others.slice(1));
  }
  const baseNum = Math.pow(10, Math.max(digitLength(num1), digitLength(num2)));
  return (times(num1, baseNum) - times(num2, baseNum)) / baseNum;
}

加法&减法的逻辑，和乘法类似，也是将数据根据最大的小数数量进行放大，再进行相加/相减，最后再进行数据缩小。

总结

• 当10进制小数转为二进制，存在无限循环时，在JavaScript中存在精度丢失
• 可通过toPrecision方法来进行精度丢失修复
• 进行数据计算时，先将小数转为整数来计算，再将结果进行放大或缩小

参考资料

• 探寻 JavaScript 精度问题以及解决方案
• JavaScript 浮点数陷阱及解法