什么是SVG?
- SVG 指可伸缩矢量图形 (Scalable Vector Graphics)
- SVG 用来定义用于网络的基于矢量的图形
- SVG 使用 XML 格式定义图形
- SVG 图像在放大或改变尺寸的情况下其图形质量不会有所损失
- SVG 是万维网联盟的标准
- SVG 与诸如 DOM 和 XSL 之类的 W3C 标准是一个整体
SVG 的历史和优势
在 2003 年一月,SVG 1.1 被确立为 W3C 标准。
参与定义 SVG 的组织有:太阳微系统、Adobe、苹果公司、IBM 以及柯达。
与其他图像格式相比,使用 SVG 的优势在于:
- SVG 可被非常多的工具读取和修改(比如记事本)
- SVG 与 JPEG 和 GIF 图像比起来,尺寸更小,且可压缩性更强。
- SVG 是可伸缩的
- SVG 图像可在任何的分辨率下被高质量地打印
- SVG 可在图像质量不下降的情况下被放大
- SVG 图像中的文本是可选的,同时也是可搜索的(很适合制作地图)
- SVG 可以与 Java 技术一起运行
- SVG 是开放的标准
- SVG 文件是纯粹的 XML
简单示例
<svg width="200" height="200" viewbox="0 0 100 100"></svg>
- width: 宽度
- height: 高度
viewBox
MDN上的说明是
看到这个说明一开始并不是很懂
我们来看一下下面这张图
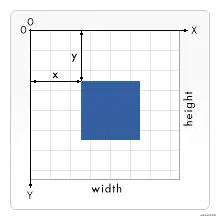
前两个参数代表x,y,画布的左上角的坐标位置。
后两个参数代表width,height,画布大小。
嵌套坐标系统
可以将另一个svg元素插入到文档中来建立一个新的视口和坐标系统,也就是说svg中可以嵌套另一个svg,每个svg都有自己独立的视口和坐标系统。
基本形状
线段
line元素,使用x1,y1,x2,y2属性指定线段的起止点坐标。有如下特性:
| 特性 | 说明 | stroke-width | 笔画宽度,坐标网格线位于笔画的正中间,可以使用css的shape-rendering值来控制反锯齿特性 | stroke | 笔画颜色 | stroke-opacity | 线条的不透明度 | stroke-dasharray | 虚线,由一系列数字组成,数字个数为偶数(负责会自动重复一遍使其为偶数),表示线长-间隙-线长-间隙... |
|---|
Demo
矩形
rect元素,使用x,y,width,height表示一个矩形
| 特性 | 说明 | fill | 填充颜色 | fill-opacity | 填充不透明度 | stroke | 边框颜色 | stroke-width | 边框宽度,边框是骑在矩形边界上的,一半在矩形外,一半在矩形内 | rx/ry | 圆角矩形,最大值为矩形宽/高的一半,如果只指定了一个,则认为两个都为相同的值 |
|---|
Demo
圆和椭圆
circle元素表示圆,由cx,cy,r属性界定 ellipse元素表示椭圆,由cx,cy,rx,ry界定
| 特性 | 说明 | fill | 填充颜色 | fill-opacity | 填充不透明度 | stroke | 边框颜色 | stroke-width | 边框宽度,边框是骑在圆的边界上的,一半在圆/椭圆外,一半在圆/椭圆内 |
|---|
Demo
路径
path命令
SVG中所有基本形状都是path的简写形式,但是建议使用简写形式,因为这样可以使SVG文档更可读。
path元素更通用,可以通过制定一系列相互连接的线、弧、曲线来绘制任意形状的轮廓,这些轮廓也可以填充或者绘制轮廓线,也可以用来定义裁剪区域或蒙版。
下表为path命令总结,其中大写表示绝对坐标,小写表示相对坐标:
| 命令 | 参数 | 说明 | M m | x y | 移动画笔到制定坐标 | L l | x y | 绘制一条到给定坐标的线 | H h | x | 绘制一条到给定x坐标的横线 | V v | y | 绘制一条到给定y坐标的垂线 | A a | rx ry x-axis-rotation large-arc sweep x y | 圆弧曲线命令有7个参数,依次表示x方向半径、y方向半径、旋转角度、大圆标识、顺逆时针标识、目标点x、目标点y。大圆标识和顺逆时针以0和1表示。0表示小圆、逆时针 | Q q | x1 y1 x y | 绘制一条从当前点到x,y控制点为x1,y1的二次贝塞尔曲线 | T t | x y | 绘制一条从当前点到x,y的光滑二次贝塞尔曲线,控制点为前一个Q命令的控制点的中心对称点,如果没有前一条则已当前点为控制点。 | C c | x1 y1 x2 y2 x y | 绘制一条从当前点到x,y控制点为x1,y1 x2,y2的三次贝塞尔曲线 | S s | x2 y2 x y | 绘制一条从当前点到x,y的光滑三次贝塞尔曲线。第一个控制点为前一个C命令的第二个控制点的中心对称点,如果没有前一条曲线,则第一个控制点为当前的点。 |
|---|
路径的填充同样可以使用fill-rule属性指定填充规则,如果需要填充一个中空的形状,则只需要注意外侧路径顺逆时针方向和内侧空心区域顺逆时针方向即可。
贝塞尔曲线
贝塞尔曲线是一种使用数学方法描述的曲线,被广泛用于计算机图形学和动画中,在矢量图里,贝塞尔曲线用于定义可无限放大的光滑曲线。
公式
线性公式
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。这条线由下式给出:

且其等同于线性插值。
二次方公式
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:

三次方公式
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
曲线的参数形式为:

现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
一般参数公式
n阶贝兹曲线可如下推断。给定点P0、P1、…、Pn,其贝兹曲线即:

如上公式可如下递归表达: 用表示由点P0、P1、…、Pn所决定的贝兹曲线。 用平常话来说,阶的贝兹曲线,即双阶贝兹曲线之间的插值。
公式说明
- 开始于P0并结束于Pn的曲线,即所谓的端点插值法属性。
- 曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线。
- 曲线的起始点(结束点)相切于贝塞尔多边形的第一节(最后一节)。
- 一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线。
- 一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时,分成四段的贝兹曲线,可以小于千分之一的最大半径误差近似于圆)。
- 位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝兹曲线精确的形成(某些琐屑实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。



看到上面的公式一头雾水,怎么办?
别急,我们不管它,继续往下看......
贝塞尔曲线绘制
贝塞尔曲线的类型有很多,但是在path元素里,只存在两种贝塞尔曲线:三次贝塞尔曲线,和二次贝塞尔曲线。
我们从稍微复杂一点的三次贝塞尔曲线C入手,三次贝塞尔曲线需要定义一个点和两个控制点,所以用C命令创建三次贝塞尔曲线,需要设置三组坐标参数:
C x1 y1, x2 y2, x y (or c dx1 dy1, dx2 dy2, dx dy)
这里的最后一个坐标(x,y)表示的是曲线的终点,另外两个坐标是控制点,(x1,y1)是起点的控制点,(x2,y2)是终点的控制点。如果你熟悉代数或者微积分的话,会更容易理解控制点,控制点描述的是曲线起始点的斜率,曲线上各个点的斜率,是从起点斜率到终点斜率的渐变过程。
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 10 C 20 20, 40 20, 50 10" stroke="black" fill="transparent"/>
<path d="M70 10 C 70 20, 120 20, 120 10" stroke="black" fill="transparent"/>
<path d="M130 10 C 120 20, 180 20, 170 10" stroke="black" fill="transparent"/>
<path d="M10 60 C 20 80, 40 80, 50 60" stroke="black" fill="transparent"/>
<path d="M70 60 C 70 80, 110 80, 110 60" stroke="black" fill="transparent"/>
<path d="M130 60 C 120 80, 180 80, 170 60" stroke="black" fill="transparent"/>
<path d="M10 110 C 20 140, 40 140, 50 110" stroke="black" fill="transparent"/>
<path d="M70 110 C 70 140, 110 140, 110 110" stroke="black" fill="transparent"/>
<path d="M130 110 C 120 140, 180 140, 170 110" stroke="black" fill="transparent"/>
</svg>
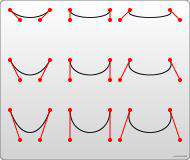
上面的例子里,创建了9个三次贝塞尔曲线。
你可以将若干个贝塞尔曲线连起来,从而创建出一条很长的平滑曲线。通常情况下,一个点某一侧的控制点是它另一侧的控制点的对称(以保持斜率不变)。这样,你可以使用一个简写的贝塞尔曲线命令S,如下所示:
S x2 y2, x y (or s dx2 dy2, dx dy)
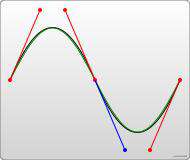
S命令可以用来创建与前面一样的贝塞尔曲线,但是,如果S命令跟在一个C或S命令后面,则它的第一个控制点会被假设成前一个命令曲线的第二个控制点的中心对称点。如果S命令单独使用,前面没有C或S命令,那当前点将作为第一个控制点。下面是S命令的语法示例,图中左侧红色标记的点对应的控制点即为蓝色标记点。
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 80 C 40 10, 65 10, 95 80 S 150 150, 180 80" stroke="black" fill="transparent"/>
</svg>
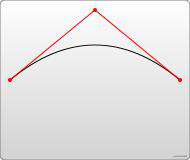
另一种可用的贝塞尔曲线是二次贝塞尔曲线Q,它比三次贝塞尔曲线简单,只需要一个控制点,用来确定起点和终点的曲线斜率。因此它需要两组参数,控制点和终点坐标。
Q x1 y1, x y (or q dx1 dy1, dx dy)
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 80 Q 95 10 180 80" stroke="black" fill="transparent"/>
</svg>
就像三次贝塞尔曲线有一个S命令,二次贝塞尔曲线有一个差不多的T命令,可以通过更简短的参数,延长二次贝塞尔曲线。
T x y (or t dx dy)
和之前一样,快捷命令T会通过前一个控制点,推断出一个新的控制点。这意味着,在你的第一个控制点后面,可以只定义终点,就创建出一个相当复杂的曲线。需要注意的是,T命令前面必须是一个Q命令,或者是另一个T命令,才能达到这种效果。如果T单独使用,那么控制点就会被认为和终点是同一个点,所以画出来的将是一条直线。
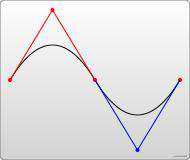
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 80 Q 52.5 10, 95 80 T 180 80" stroke="black" fill="transparent"/>
</svg>
虽然三次贝塞尔曲线拥有更大的自由度,但是两种曲线能达到的效果总是差不多的。具体使用哪种曲线,通常取决于需求,以及对曲线对称性的依赖程度。
Demo
下面提供了两个网址,大家可以尝试绘制自己的贝塞尔曲线:
贝塞尔曲线编辑器
高阶贝塞尔曲线编辑器
SVG 动画
CSS动画
现代浏览器都支持CSS梳理SVG动画,使用CSS处理SVG动画需要两个步骤:一是选中要运动的元素,然后设置将动画属性作为一个整体进行设置。二是告诉浏览器改变选中元素的哪个属性以及在动画的什么阶段。这些都定义在@keyframes说明符中。
下面我们来实现一个大小动态变化的圆:
const x = 100;
const y = 100;
const radius = 20;
const outerRadius = radius * 2.2;
const color = '#5ac1dc';
return (
<svg width="200" height="200" viewBox="0 0 200 200">
<defs>
<style>{`
.gs-service-dot-inner{animation:scaleDot 2s infinite;}
.gs-service-dot-outer{opacity:0.27;animation:scaleDot 2s infinite;}
@keyframes scaleDot {
0%{transform: scale(1);}
50%{transform: scale(1.3);}
100%{transform: scale(1);}
}`}</style>
</defs>
<circle
key="inner"
className="gs-service-dot-inner"
cx={x}
cy={y}
r={radius}
fill={color}
style={{ transformOrigin: `${x}px ${y}px` }}
/>
<circle
key="outer"
className="gs-service-dot-outer"
cx={x}
cy={y}
r={outerRadius}
fill={color}
style={{ transformOrigin: `${x}px ${y}px` }}
/>
</svg>
);
Demo
如何画一条会动的曲线
我们需要用到两个属性
- stroke-dasharray 可控制用来描边的点划线的图案范式。该属性是让你指定画出的线段每段的长度,第二个值是各段之间空隙的长度。
- stroke-dashoffset 属性指定了dash模式到路径开始的距离。该属性是让你指定每个小段的起始偏移量。
<path stroke="#000" stroke-width="4.3" fill="none" d="…"
stroke-dasharray="988.00 988.00"
stroke-dashoffset="988.00"
/>
请将两个属性都设到最大值(线的总长度),然后缓慢的减少dashoffset属性值。哇塞,线被动态的画出来了!
线的长度你可以从DOM里获取:
var path = document.querySelector('.squiggle-container path');
path.getTotalLength();
之后你就可以使用CSS动画来减少dashoffset属性值,让线动态的画出来了。
Demo
自己尝试一下拖动修改这两个属性
(未完待续)
参考文献:
MDN SVG 路径
SVG技术入门:如何画出一条会动的线
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?





发表评论
还没有评论,快来抢沙发吧!