动态规划巧解凑零钱问题 | 创作者训练营

状态转移方程，最重要的是先找到状态，然后将「大问题」转换成「小问题」，将「全局问题」转换成「局部问题」。转换的过程用表达式写出来，即是状态转移方程。

我们通常使用 DP （Dynamic Programming）表示状态转移方程。

题目

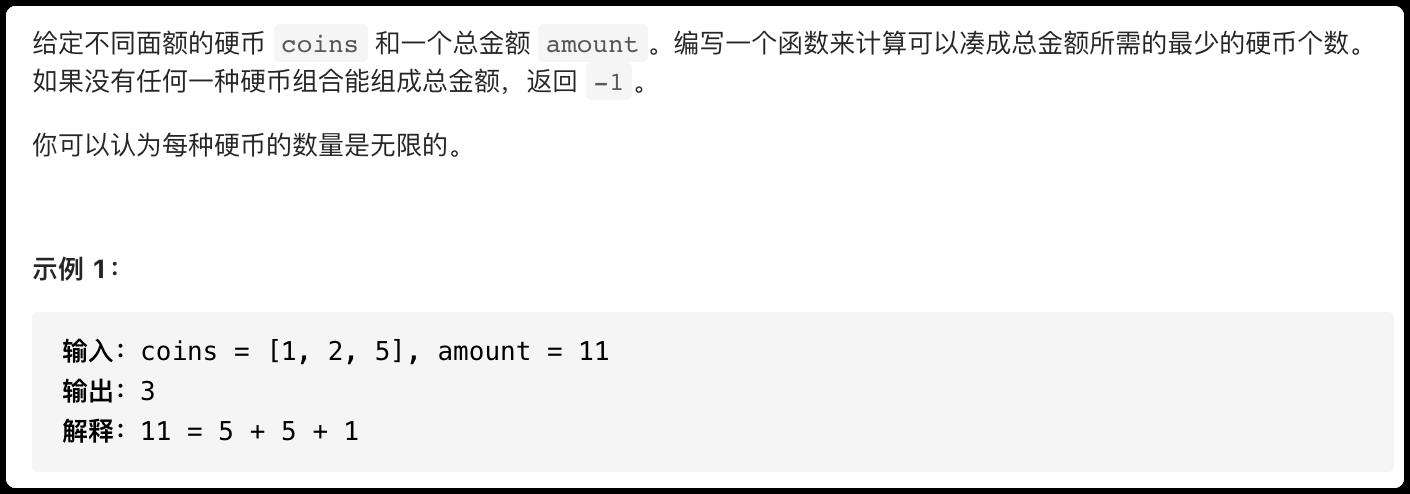
分析

题目要求凑出给定金额最少的硬币数，这是个唯一的状态。每次选择不同面额的硬币会影响这个状态的变化。 我们使用 dp(n) 表示凑出 n 元，最少所需的硬币个数。此时可以归纳出一个状态：

dp(n) = dp(n-coin) + 1

凑出 n 元最少所需要的硬币数，等于凑出（n-coin） 元最少所需的硬币数目，加上最后的 coin 这一枚。

边界条件有两个：

1. dp(0) = 0 // 凑出 0 元，不需要硬币
2. dp(n < 0) = -1 // 金额小于 0，直接返回 -1

其中，我们使用一个 map 储存已经计算过金额的最优解，防止重复计算。

实现

const coinChange = (coins, amount) => {
  let map = {};
  
  function dp(amount){
    if(amount == 0) return 0;
    if(amount < 0) return -1;
    if(map[amount]) return map[amount];
    let count = Number.MAX_SAFE_INTEGER;
    
    //遍历每一种情况
    for(let coin of coins) {
      const sub = dp(amount - coin);
      // 条件表示某一种可行解
      // 如果递归到最后返回 -1 ，表示当前的组合不是可行解
      // 凑不出来这种组合，这种组合需要排除
      if( sub > -1) {
        // 更新 count 
        count = Math.min(count, sub+1)
      }
    }
    map[amount] = count;

    // 不可以直接返回 count，因为存在硬币都匹配不到情况的，此时我们要
    // 将默认的 count 改成 -1 返回
    // return count
    return count == Number.MAX_SAFE_INTEGER ? -1 : count;
    
  }
  
  return dp(amount);
}

「 一枚前端学习小透明，努力学习前端知识，同时分享自己对生活的一些思考，欢迎一起讨论交流。如果我的文章对你有帮助，请点个赞，会非常感恩你的鼓励。完」

创作者训练营 征文活动正在进行中......