jsliang 求职系列 - 44 - 算法系列汇总

一 目录

不折腾的前端，和咸鱼有什么区别

二 前言

前端，入门难；前端，要搞好很难。

现在面试我也是随缘刷题了，虽然在动态规划、贪心算法上有一些缺陷，不过对于字符串、数组、栈、队列、链表、树、深度优先搜索、广度优先搜索、回溯、滑动窗口、双指针等题目来说，我还是可以应付的。

按照每天刷一道题，一道题 15min~2h 来说，一瞬间复习完面试可能出现的算法与数据结构，我感觉是不太科学的。

如果小伙伴希望一夜全懂，那 —— 如果能重来，我要选李白~

建议复习下各种排序算法以及查找算法，然后看看红黑树或者 AVL 树，其他就真的随缘了，如果你平时没怎么接触算法与数据结构的话，要一下子懂那么多，还是有些难度的。

一起加油吧！

三 收集题库

下面这些都是收集的，面市场上出现过的一些题目，感兴趣的可以看看，有些已经贴出 LeetCode 的地址：

1. 快速排序
2. 实现一个算法，来完成字符串相加，比如 '111' + '2222' = '2333'。(高精度算法)
3. 有一个 '123456789101112131415....n+1' 类似这样的序列，求出第 m 位的数字，例如 m = 11 -> 输出 0，m = 12 -> 输出 1
4. 有一个有序递增序列，求有多少个不同的数字。比如 [1, 5, 7, 7, 8, 9, 9]。里面总共有 5 个不同的数字：[1, 5, 7, 8, 9]
5. 红黑树和哈希表的对比
6. 哈希表如何解决冲突
7. 非递归实现树的后序遍历
8. 350-两个数组的交集 II
9. 611-有效三角形的个数
10. 659-分割数组为连续子序列
11. 接雨水。给定数组 [1, 8, 6, 2, 5, 4, 8, 3, 7]，表示容器能容纳水的最大值。
12. 写一个数组去重。O(n^2) 及 O(n) 时间复杂度实现
13. 我现在有一个数组 [1,2,3,4]，请实现算法，得到这个数组的全排列的数组，如 [2,1,3,4]，[2,1,4,3]，你这个算法的时间复杂度是多少？
14. 我现在有一个背包，容量为 m，然后有 n 个货物，重量分别为 w1,w2,w3...wn，每个货物的价值是 v1,v2,v3...vn，w 和 v 没有任何关系，请求背包能装下的最大价值。
15. 二叉树的遍历方式和特点
16. 排序算法及其原理（手写）
17. 104-二叉树的最大深度
18. 572-另一个树的子树
19. 100-相同的树
20. 226-翻转二叉树
21. 509-斐波那契数
22. 88-合并两个有序数组
23. 384-打乱数组
24. 56-合并区间

四 下划线转驼峰

实现一个方法，将传入对象的下划线命名方式全部换为驼峰式（考虑递归的场景）

const obj = {
  my_name: 'jsliang',
  wo_de_jia: {
    zu_fang: 'guangzhou',
    jia: 'heyuan',
    zu_ji: 'maoming',
  },
};

/*
转换为：
{
  myName: 'jsliang',
  woDeJia: { jia: 'heyuan', zuFang: 'guangzhou', zuJi: 'maoming' },
}
*/

const getType = arg => Object.prototype.toString.call(arg).slice(8, -1);

const changeCamel = str => str.split('_').map((item, index) => index === 0 ? item : item.slice(0, 1).toUpperCase() + item.slice(1)).join('');

const change = (obj) => {
  for (let i in obj) {
    if (obj.hasOwnProperty(i)) {
      if (getType(obj[i]) === 'Object' && i.includes('_')) {
        const now = changeCamel(i);
        obj[now] = obj[i];
        delete obj[i];
        change(obj[now]);
      } else if (getType(obj[i]) === 'Object') {
        change(obj[i]);
      } else if (i.includes('_')) {
        const now = changeCamel(i);
        obj[now] = obj[i];
        delete obj[i];
      }
    }
  }

  return obj;
};

console.log(change(obj));

五 冒泡排序

说起冒泡排序，jsliang 可以细细哆嗦。

下面的排序，我们讲的都是【顺序排序】，即 [1, 2, 3, 4]

所谓冒泡，就是将数组中的数字两两比对，每次将较大的数字往后移，较小的数字往数组头部移动，从而看起来似小气泡往水面浮起。

就好比数组 [3, 2, 1]：

1. 将 3 往后移，变成 [2, 1, 3]
2. 将 2 往后移，变成 [1, 2, 3]

当然，同样的冒泡排序方法，也是有不同的方式的。

这里讲 3 种方法，希望你能看懂。

5.1 解法一

1. 双重循环
2. i 表示当前数字，j = i + 1
3. 表示第 i 次的时候和后面的数字逐个比对

console.log('解法一');
const bubbleSortOne = (arr) => {
  let time = 0;

  for (let i = 0; i < arr.length - 1; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      time++;
      if (arr[i] > arr[j]) {
        [arr[i], arr[j]] = [arr[j], arr[i]];
      }
    }
  }

  return [arr, time];
};

console.log(bubbleSortOne([1, 2, 3])); // [ [ 1, 2, 3 ], 3 ]
console.log(bubbleSortOne([1, 3, 2])); // [ [ 1, 2, 3 ], 3 ]
console.log(bubbleSortOne([3, 2, 1])); // [ [ 1, 2, 3 ], 3 ]

5.2 解法二

• i 表示第几轮
• j 表示前后比较的数字
• 每次拿 j 和 j + 1 的数字对比

console.log('解法二：');
const bubbleSortTwo = (arr) => {
  let time = 0;

  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      time++;
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }

  return [arr, time];
};

console.log(bubbleSortTwo([1, 2, 3])); // [ [ 1, 2, 3 ], 3 ]
console.log(bubbleSortTwo([1, 3, 2])); // [ [ 1, 2, 3 ], 3 ]
console.log(bubbleSortTwo([3, 2, 1])); // [ [ 1, 2, 3 ], 3 ]

5.3 解法三

• 大体同解法二
• 优化点在于 flag
• 如果某一轮没发生对比，那么中止循环

console.log('解法三：');
const bubbleSortThree = (arr) => {
  let time = 0;

  for (let i = 0; i < arr.length; i++) {
    let flag = false;
    for (let j = 0; j < arr.length - i - 1; j++) {
      time++;
      if (arr[j] > arr[j + 1]) {
        flag = true;
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
    if (!flag) {
      return [arr, time];
    }
  }

  return [arr, time];
}

console.log(bubbleSortThree([1, 2, 3])); // [ [ 1, 2, 3 ], 2 ]
console.log(bubbleSortThree([1, 3, 2])); // [ [ 1, 2, 3 ], 3 ]
console.log(bubbleSortThree([3, 2, 1])); // [ [ 1, 2, 3 ], 3 ]

六 选择排序

选择排序，每次遍历，选择最大或者最小的数字进行替换。

6.1 选择排序写法

const selectSort = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    let min = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[min]) {
        min = j;
      }
    }
    [arr[min], arr[i]] = [arr[i], arr[min]];
  }

  return arr;
};

console.log(selectSort([7, 1, 3, 2, 5, 4, 7, 6, 1])); // [1, 1, 2, 3, 4, 5, 6, 7, 7]

6.2 二元排序

在选择排序中，我们每次都选择最小或者最大的的排在数组开头，这是使用了一个元素，假如我们将最大值和最小值都查找出来，效率就会提升一倍！

const twoSort = (arr) => {

  const length = arr.length;

  for (let i = 0; i < length / 2; i++) {
    let minIndex = i, maxIndex = i;
    for (let j = i + 1; j < length - i; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
      if (arr[j] > arr[maxIndex]) {
        maxIndex = j;
      }
    }
    [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    
    // 如果最大值的下标等于 i，也就是说 arr[i] 就是最大值
    // 由于 arr[i] 是当前遍历轮次的首位，它已经和 arr[minIndex] 交换了
    // 所以最大值的下标需要跟踪到 arr[i] 最新的下标 minIndex。
    if (maxIndex === i) {
      maxIndex = minIndex;
    }

    [arr[length - i - 1], arr[maxIndex]] = [arr[maxIndex], arr[length - i - 1]];
    console.log(arr);
  }

  return arr;
};

console.log(twoSort([7, 3, 2, 4, 6, 5, 1])); // [ 1, 2, 3, 4, 5, 6, 7 ]

当然，优化之后效率虽然提升了，但是时间复杂度没有发生改变。

时间复杂度跟常量无关，所以 O(n^2) 处于 2 还是 O(n^2)。

七 排序算法的稳定性

在学习了解了冒泡排序和选择排序之后，我们来比较下这两者的异同点。

相同点：

• 都是两层循环，时间复杂度都为 O(n^2)
• 都只使用有限个变量，时间复杂度 O(1)

不同点：

• 冒泡排序在比较过程中就不停交换
• 选择排序增加了一个变量保存最小值/最大值的下标，遍历完成后才交换，减少了交换次数

实际上，这两者还有一个不同点：

• 冒泡排序是稳定的，选择排序是不稳定的

假设有数组 [2, 2, 1]。

在冒泡排序中，只有左边的数字大于右边的数字，才会发生交换，相同的数字之间不会发生交换，所以它是稳定的。

而选择排序中，最小值和首位交换的过程会破坏稳定性，比如上面的数组，在选择排序中第一次交换时，原数列中的两个 2 的相对顺序就被改变了，因此它是不稳定的。

所以到底怎么理解稳定和不稳定呢？

• 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

排序算法的稳定性意义何在？

• 当要排序的内容是一个对象的多个数字属性，且其原本的顺序存在意义时，如果我们需要在二次排序后保持原有排序的意义，就需要使用到稳定性的算法。

八 插入排序

所谓插入排序，就是每次将当前数字插入到前面已经排好队的合适位置。

例如有数组：[5, 3, 1, 2, 4]，那么它在插入排序中表现如下：

1. 5，前面没有其他数字了，所以不需要插入操作
2. 3，前面有个 5，而 3 < 5，所以将它插入到前一个数字去，变成 [3, 5, 1, 2, 4]
3. 1，前面有 [3, 5]，那么逐步遍历，将它插入到第一个位去，变成 [1, 3, 5, 2, 4]
4. 2，前面有 [1, 3, 5]，插入后变成 [1, 2, 3, 5, 4]
5. 4，最后输出成 [1, 2, 3, 4, 5]

哆嗦无益，看代码：

const twoSort = (arr) => {
  const length = arr.length;

  for (let i = 1; i < length; i++) {
    const currentNumber = arr[i];

    let j = i - 1;

    while (j >= 0 && currentNumber < arr[j]) {
      arr[j + 1] = arr[j];
      j--;
    }

    arr[j + 1] = currentNumber;
  }

  return arr;
};

console.log(twoSort([7, 3, 2, 4, 6, 5, 1])); // [ 1, 2, 3, 4, 5, 6, 7 ]

九 快速排序

快速排序，就是面试常问的快排。

在平均情况下，排序 n 个项目要 O(nLogn) 次比较；在最坏情况下，需要 O(n^2) 次比较。

快速排序大概需要 3 步骤：

1. 选择元素作为基准点
2. 排序数组，比基准值小的放左边，大于的放右边，基准值在中间
3. 递归重复步骤 1 和步骤 2

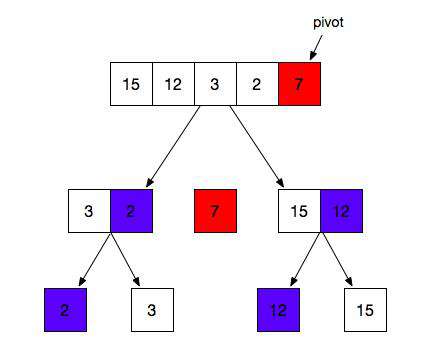
9.1 方法一：基础思路

下面这种方法提供了一种思路，但是面试建议别用这种方法回答。

1. 如果数组剩下一个以下，那就返回数组
2. 如果数组有 2 个及以上，那么设置中间点 mid
3. 通过 forEach 遍历，将小于中间点 mid 的放左边 left，大于中间点 mid 的放右边 right
4. 返回重组后的数组 [...quickSort(left), mid, ...quickSort(right)]

const quickSort = (arr) => {
  if (arr.length <= 1) {
    return arr;
  }
  const midIndex = Math.floor(arr.length / 2);
  const mid = arr.splice(midIndex, 1)[0];
  const left = [];
  const right = [];
  arr.forEach(item => item < mid ? left.push(item) : right.push(item));
  return [...quickSort(left), mid, ...quickSort(right)];
};

console.log(quickSort([7, 1, 3, 2, 5, 4, 7, 6, 1])); // [ 1, 1, 2, 3, 4, 5, 6, 7, 7 ]

9.2 方法二：优化

下面这种快排属于简单一点的快排。

1. 设置左右边界 left = 0，right = arr.length - 1
2. 每次都将右边的数字作为基数
3. 小于基数的放左边
4. 大于基数的放右边
5. arr[pos] 位置就是本次排列好的数字
6. 递归 quickSort(arr, left, pos - 1)，quickSort(arr, pos + 1, right)

const quickSort = (arr, left = 0, right = arr.length - 1) => {
  if (left < right) {
    let pos = left - 1;

    const rightVal = arr[right];

    for (let i = left; i <= right; i++) {
      if (arr[i] <= rightVal) {
        pos++;

        [arr[i], arr[pos]] = [arr[pos], arr[i]];
      }
    }

    quickSort(arr, left, pos - 1);
    quickSort(arr, pos + 1, right);
  }

  return arr;
};

console.log(quickSort([7, 1, 3, 2, 5, 4, 7, 6, 1])); // [1, 1, 2, 3, 4, 5, 6, 7, 7]

这种快排欠缺 2 个考虑：

1. 有序数组的情况。如果当前数组已经有序了，那就不需要进一步递归了。
2. 大量重复数据的情况。如果当前数组重复数据较多，那么比较难保证递归两遍的数组平衡。

9.3 方法三：三路快排

三路快速排序是快速排序的的一个优化版本，将数组分成三段，即小于基准元素、等于基准元素和大于基准元素，这样可以比较高效的处理数组中存在相同元素的情况，其它特征与快速排序基本相同。

const quickSort = (arr, left = 0, right = arr.length - 1) => {
  if (left < right) {

    let leftPos = left - 1;

    let middlePos = 0;

    const compareValue = arr[right];

    for (let i = left; i <= right; i++) {
      if (arr[i] <= compareValue) {
        leftPos++;
        [arr[i], arr[leftPos]] = [arr[leftPos], arr[i]];
        if (arr[i] === compareValue) {
          middlePos++;
        }
      }
    }

    quickSort(arr, 0, leftPos - 1);
    quickSort(arr, leftPos + middlePos, right);
  }

  return arr;
}

console.log(quickSort([7, 2, 3, 3, 2, 4, 5, 4, 7, 6, 5, 1])); // [ 1, 2, 3, 4, 5, 6, 7 ]

十 归并排序

归并排序和快排的思路类似，都是递归分治，区别在于快排边分区边排序，而归并在分区完成后才会排序。

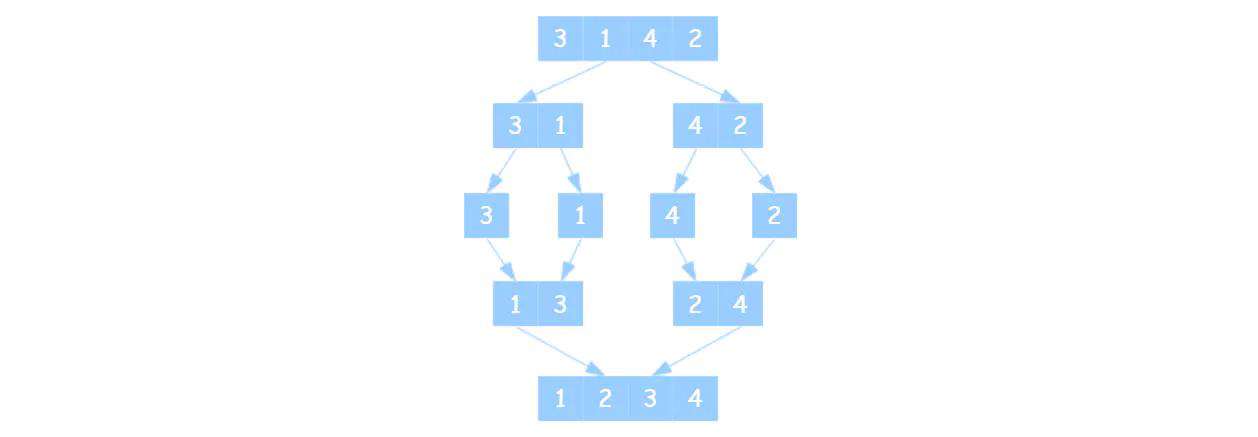
const mergeSort = (arr) => {
  if (arr.length <= 1) {
    return arr;
  }

  const midIndex = Math.floor(arr.length / 2);
  const left = arr.slice(0, midIndex);
  const right = arr.splice(midIndex, arr.length);

  return merge(mergeSort(left), mergeSort(right));
};

const merge = (left, right) => {
  const result = [];

  while (left.length && right.length) {
    if (left[0] < right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }

  while (left.length) {
    result.push(left.shift());
  }

  while (right.length) {
    result.push(right.shift());
  }

  return result;
};

console.log(mergeSort([3, 1, 4, 2])); // [1, 2, 3, 4]

十一 排序算法时间复杂度

从表格中我们可以看到，就时间复杂度而言，快排并没有很大优势。

然而为什么快排会成为最常用的排序手段，这是因为时间复杂度只能说明随着数据量的增加，算法时间代价增长的趋势，并不直接代表实际执行时间，实际运行时间还包括了很多常数参数的差别。

此外，在面对不同类型数据(比如有序数据、大量重复数据)时，表现也不同，综合来说，快排的时间效率是最高的。

在实际运用中, 并不只使用一种排序手段, 例如 V8 的 Array.sort() 就采取了当 n<=10 时, 采用插入排序, 当 n>10 时，采用三路快排的排序策略。

十二 查找

在算法与数据结构中，查找一个数字，要快准狠。

12.1 顺序遍历

这是最普通的一种查找方式，时间复杂度 O(n)，即最多需要遍历完整个数组。

const search = (arr, target) => {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === target) {
      return i;
    }
  }
  return -1;
}

console.log(search([1, 3, 2, 5, 4, 7, 6], 7));

12.2 双指针

相比起顺序遍历的 O(n) 复杂度，我们加多了一个指针，通过 left = 0, right = arr.length - 1 这样子，让左右指针不停往中间移动，从而更快查找到元素。

相比顺序遍历，此时的搜索速度 * 2。

const doubleSearch = (arr, target) => {
  for (let i = 0, j = arr.length - 1; i <= j; i++, j--) {
    if (arr[i] === target) {
      return i;
    } else if (arr[j] === target) {
      return j;
    }
  }
  return -1;
}

console.log(doubleSearch([1, 3, 2, 5, 4, 7, 6], 5));

12.3 二分查找

用来查找【已排序】的顺序数组。

1. 划分左右：left 和 right
2. 每次查找中间元素 mid：Math.floor((left + right) / 2)
3. 如果 arr[min] 是需要查找的元素，返回 mid 位置
4. 如果 arr[min] > target，那么让 right = mid - 1
5. 如果 arr[min] < target，那么让 left = mid + 1
6. 循环步骤 2~步骤 5，直到 left <= right 不成立

const binarySearch = (arr, target) => {
  let left = 0;
  let right = arr.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    if (arr[mid] === target) {
      return mid;
    } else if (arr[mid] > target) {
      right = mid - 1;
    } else if (arr[mid] < target) {
      left = mid + 1;
    }
  }

  return -1;
};

console.log(binarySearch([0, 1, 2, 3, 4, 5, 6], 1));
console.log(binarySearch([0, 1, 2, 3, 4, 5], 0));

十三 参考文献

本系列有 14 篇参考文献。

• 排序算法【阅读建议：1h】

刷题：

• LeetBook - 字节跳动【阅读建议：无】

学习：

• (1.8w字)负重前行，前端工程师如何系统练习数据结构和算法？【阅读建议：无】
• 动画详解常用排序算法（1）【阅读建议：30min】
• 模板不重要【阅读建议：10min】
• 更新！万字长文带你拿下九大排序的原理、Java 实现以及算法分析【阅读建议：1h】
• JS中的算法与数据结构——链表(Linked-list)【阅读建议：30min】
• 前端你应该了解的数据结构与算法【阅读建议：30min】
• 数据结构与算法在前端领域的应用 - 第二篇【阅读建议：30min】
• JavaScript 数据结构与算法之美【阅读建议：无】
• 前端笔试&面试爬坑系列---算法【阅读建议：30min】
• 漫画：什么是红黑树【阅读建议：1h】
• 6k字 | 红黑树上红黑果，红黑树下你和我 —— 红黑树入门【阅读建议：30min】

题目：

• 一年半前端跳槽面试经验（头条、微信、shopee）【阅读建议：无】