深度优先搜索
- 深度优先搜索算法将会
从第一个指定的顶点开始遍历图,沿着路径直到这条路径的最后一个顶点被访问了,接着按照原路回退并探索下一条路径。 - 也就是说,它是先深度后广度地访问顶点。
- 注意:深度优先搜索,不需要一个源顶点。(因为它是沿着路径去探索的)
深度优先搜索的步骤是递归的。这也就意味着:深度优先搜索算法使用栈来存储函数调用(由递归调用所创建的栈)。- 类似于之前的广度优先搜索,我们同样适用颜色来标记顶点的访问探索情况:
- 被发现的顶点标记为灰色;
- 已被探索的顶点标记为黑色;
实现
- 准备工作
// 将图的所有顶点全部初始化为白色
const colors = {
white: 0,
gray: 1,
black: 2
}
const initializeColor = vertices => {
const color = {};
for (let i = 0; i < vertices.length; i++) {
color[vertices[i]] = colors.white;
}
return color;
};
- 开始干活
this.dfs = function(callback) {
// 拿到所有已经初始化好的顶点及其颜色的集合
let color = initializeColor()
// 定义递归函数
let dfsVisit = function(u, color, callback) {
// 将遍历到的未访问的顶点u 标记为 灰色,代表已访问到
color[u] = 'gray';
if (callback) {
callback(u)
}
// adjList字典中存储的是顶点和它的邻接顶点列表,所以我们拿到顶点u的邻接列表
let neighbors = adjList.get(u);
// 循环拿到的顶点u的邻接顶点列表
for (let i = 0; i < neighbors.length; i++) {
// 取出每个邻接顶点
let w = neighbors[i]
// 如果该邻接顶点是未被访问过的,即白色,那么就调用 dfsVisit方法,再次探索
if (color[w] === 'white') {
dfsVisit(w, color, callback)
}
}
// 最后,该顶点和邻接顶点按深度访问完之后,回退,表示该顶点已被完全探索,并将其标记为黑色
color[u] = 'black';
}
// 遍历所有顶点,对每个未访问的顶点调用私有的递归函数
for (let i = 0; i < vertices.length; i++) {
if(color[vertices[i]] === 'white') {
dfsVisit(vertices[i], color, callback);
}
}
}
- 附上一张过程图:
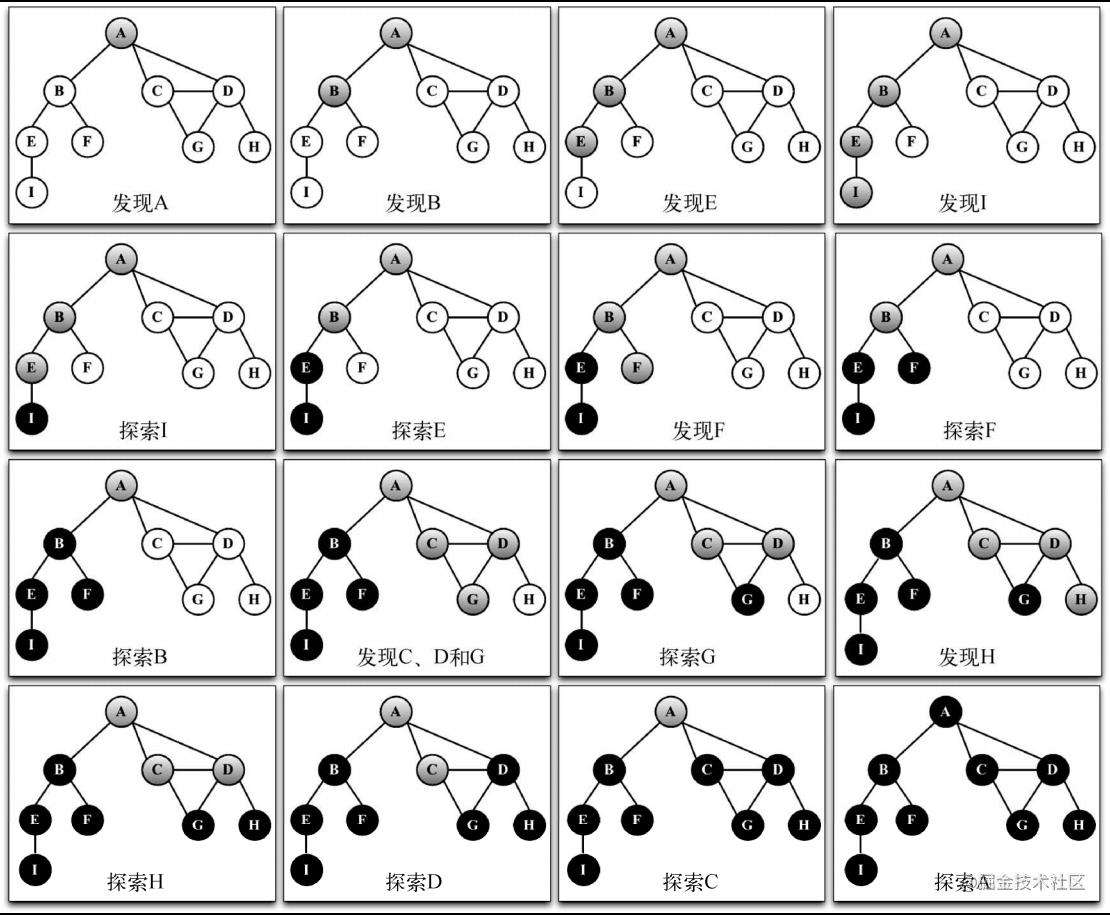
解析:
- 因为我们在之前的文章中,创建 vertices 数组时,是用来存储 图的所有顶点的。而我们在创建该数组是是将
A B C D E F G H I顶点依次push进数组的,所以在深度优先搜索时,我们会在上图中看到第一个标记为灰色的顶点是A。 - 将A标记为灰色之后,遍历了A的邻接顶点列表
['B', 'C', 'D'],此时第一次循环拿到了 顶点B,结果发现B此时是白色的; - 那么 就调用 dfsVisit方法,将
B标记为 灰色;此时拿到了 B的邻接顶点列表['E', 'F'],遍历该列表,第一次拿到了顶点E,发现它是白色的; - 接着 调用 dfsVisit方法,将
E标记为 灰色;此时拿到了E的邻接顶点列表['I'],遍历该列表,拿到了顶点I,发现它是白色的; - 接着 调用 dfsVisit方法,将
I标记为 灰色;结果发现此时 I的邻接列表没了,也就意味着,我们这条路径已经完全探索完毕啦,此时将顶点 I 标记为 黑色。 - 然后
['E', 'F']第二次拿到了F,发现它是白色的; - 接着 调用 dfsVisit方法,将
F标记为 灰色;此时 F的邻接列表为['B'],遍历该列表,发现 B是灰色的,则F的邻接列表探索完毕,将 F 标记为黑色。 - 开始回退。
- 依此类推。
- 送上一张手绘图,帮助理解。
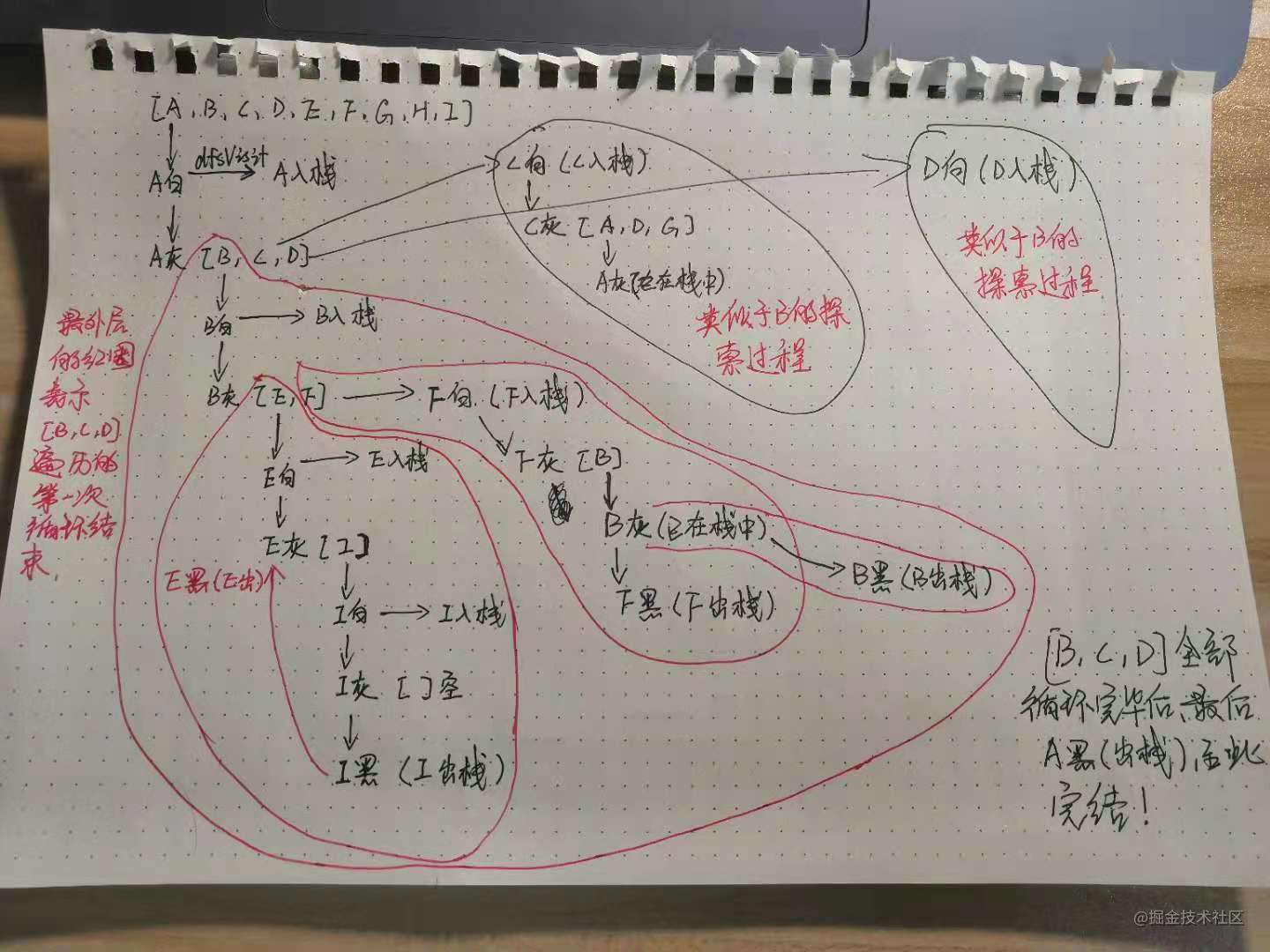
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!