第一讲:保密学基础
1:保密学的基本概念
什么是保密学?
其他相关概念
| 名词 | 概念 | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 明文 | 需要被隐蔽的消息 | 密文 | 明文经密码变换成的一种隐蔽形式 | 加密 | 将明文变换为密文的过程 | 解密 | 加密的逆过程 | 加密员 | 对密码进行操作的人员 | 加密算法 | 密码员对明文进行加密时所采用的一种规则 | 接收者 | 传送消息的预定对象 | 解密算法 | 接收者对密文进行解密时所采用的一组规则 | 密钥 | 控制加密和解密算法操作的数据处理,分别称作加密密钥和解密密钥 | 截收者 | 在信息传输和处理系统中的非授权者,通过搭线窃听、电磁窃听、等来窃取机密信息 | 密码分析 | 截收者试图通过分析从截获的密文推断出原来的明文或密钥 | 密码分析员 | 从事密码分析的人 | 被动攻击 | 对一个保密系统采取截获密文进行分析的攻击 | 主动攻击 | 攻击者主动向系统窜扰,采用删除,伪造等篡改手段,向系统注入假消息,达到自己的目的 |
保密系统模型图
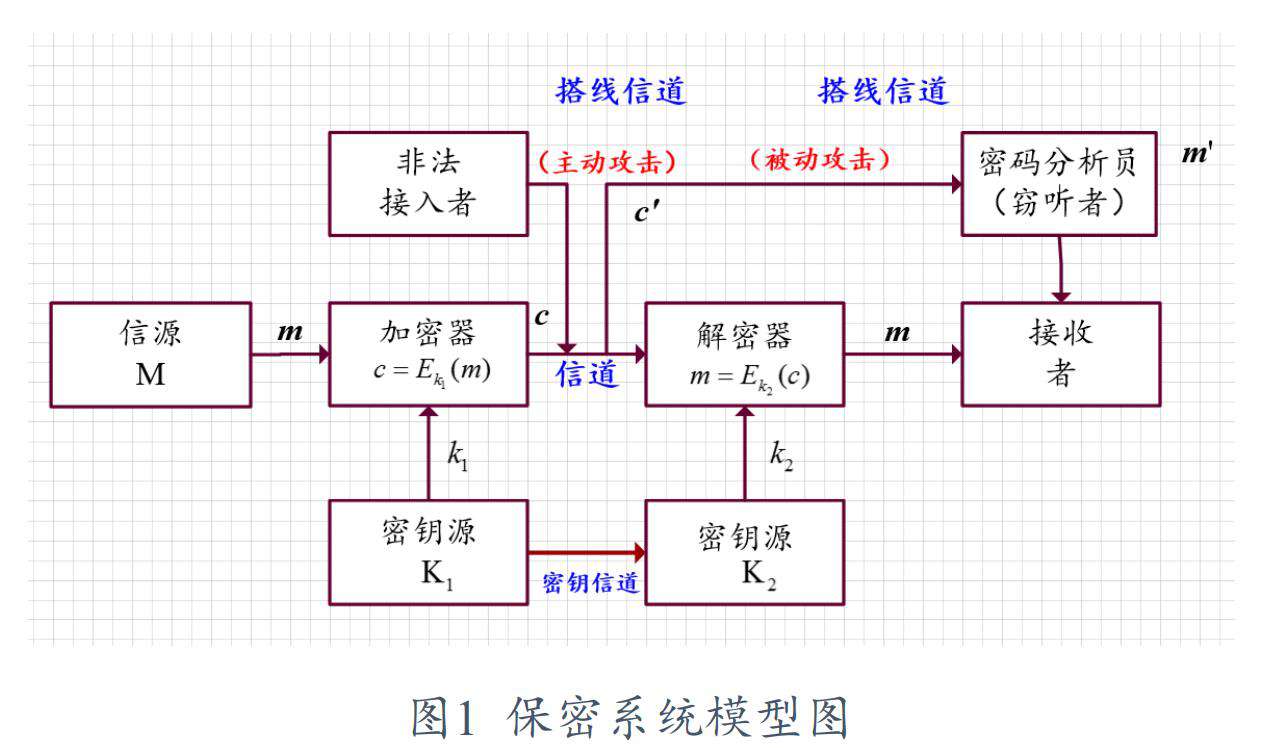
从上图我们可以看出,加密器和解密器分别对应一个密钥,主动攻击是从信道进行介入的,被动攻击也是从信道进行窃听的。
保密系统相关参数解读
1:明文消息空间M
2:密文消息空间C
3:密钥空间K1和K2、在单钥体制下,K=K1=K2,此时密钥k∈K,需经安全的密钥信道由发方传给收方。
4:加密变换与解密变换见下图。
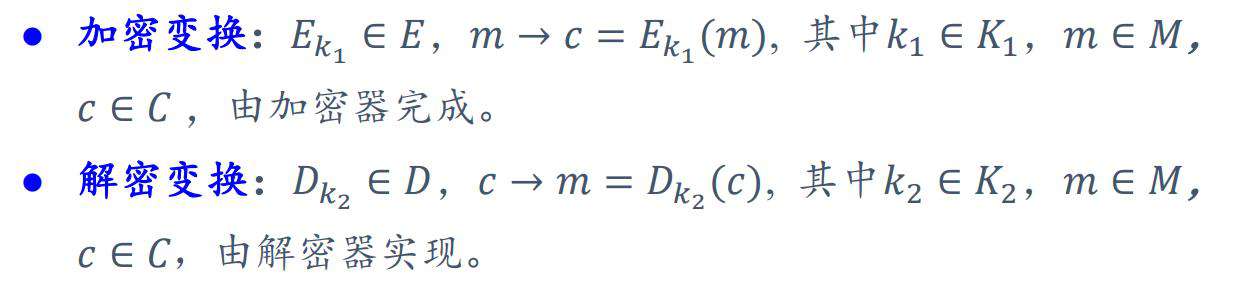
保密系统应当满足的要求
| 序号 | 要求 | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 系统即使理论上可破,也应该为实际上不可破,即从截获的密文或某些已知明文密文对,要决定密钥或任意明文在计算上是不可行的。 | 2 | 系统的保密性靠的不是加密体制或算法,而是密钥 | 3 | 加密和解密算法适用于所有密钥空间中的元素 | 4 | 系统便于实现和使用方便 |
认证与认证系统
- 认证系统
- 保密性
- 认证性
安全认证系统应当满足下面四个条件
| 序号 | 条件 | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 合法接收者能够检验消息的合法性和真实性 | 2 | 消息的发送者对所发送的消息不能依赖 | 3 | 除了合法的消息发送者之外,其他人不能伪造合法的消息,而且在已经明文和密文的情况下不能推断出密钥和伪造密文 | 4 | 必要时可由第三方做出仲裁 |
完整性
2:密码体制分类
密码体制分类
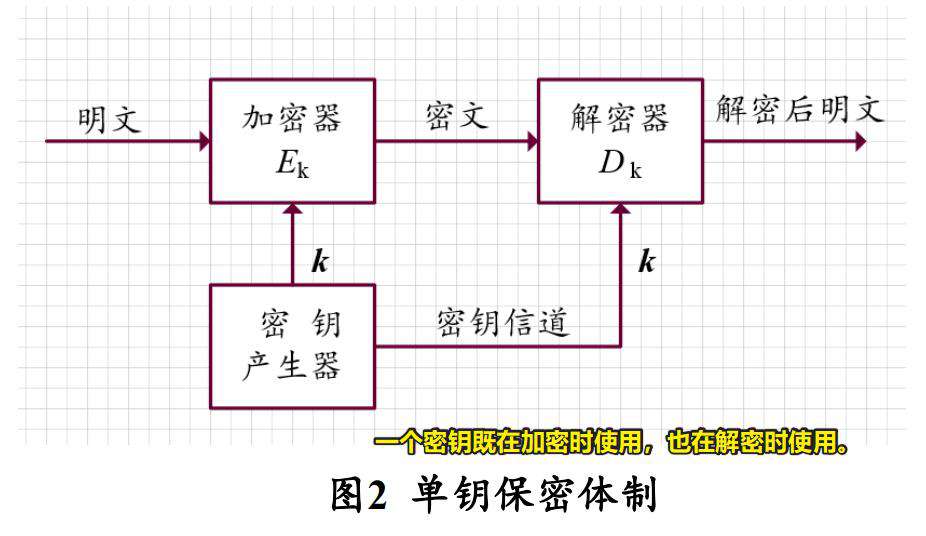
- 单钥体制:加密密钥和解密密钥相同。
- 双钥体制:加密密钥和解密密钥不同。
单钥体制的两个主要方面
- 密钥产生
- 密钥管理
单钥保密体制流程图
单钥体制的分类
- 流密码
- 分组密码
单钥体制不仅可以用于数据加密,也可用于消息的认证。
什么是公钥体制(也叫双钥体制)?
Diffie和Hellman1976年首次提出,每个用户都有一对选定的密钥(公钥K1和私钥K2),公开的密钥K1可以像电话号码一样进行公布。
- 双钥体制是如何进行加解密的?
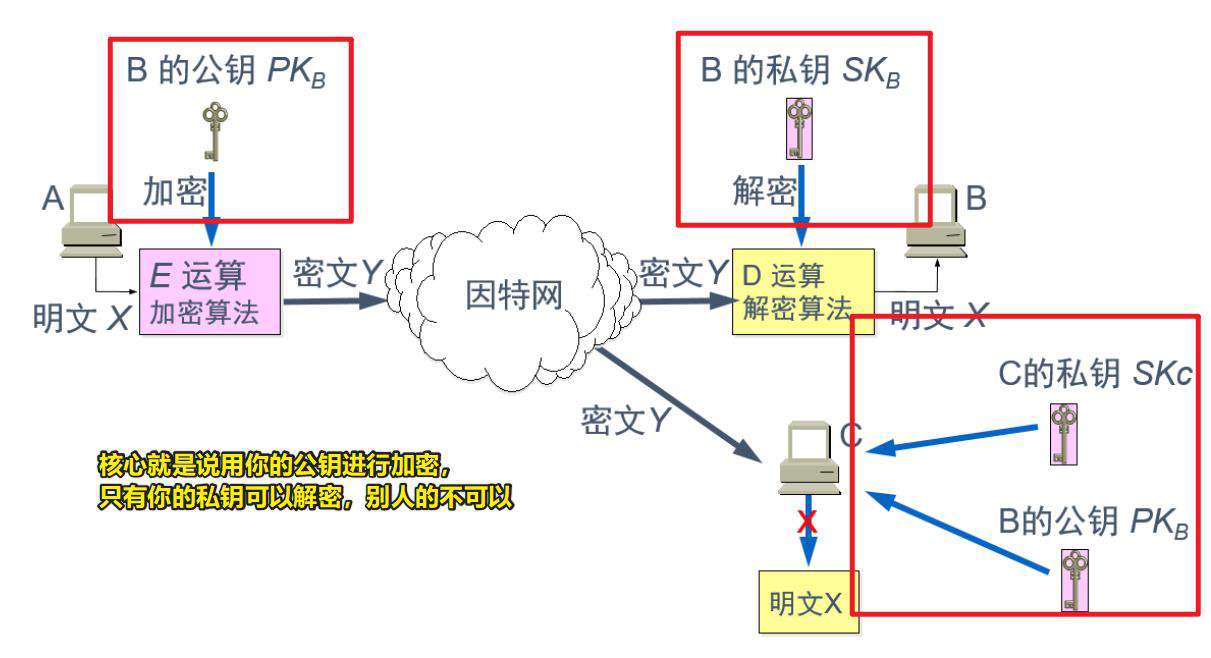
此图的参考文献,大佬的文章讲的确实不错
公钥体制的主要特点:加密和解密的能力分开
- 公钥加密私钥解密:多个用户加密的消息,只能由一个用户进行解读,可用于公共网络中实现保密通信。
- 私钥加密公钥解密 :只能由一个用户加密消息,而使多个用户可以解读,可用于认证系统中对消息进行数字签名。
- 无需事先分配密钥。
双钥保密体制
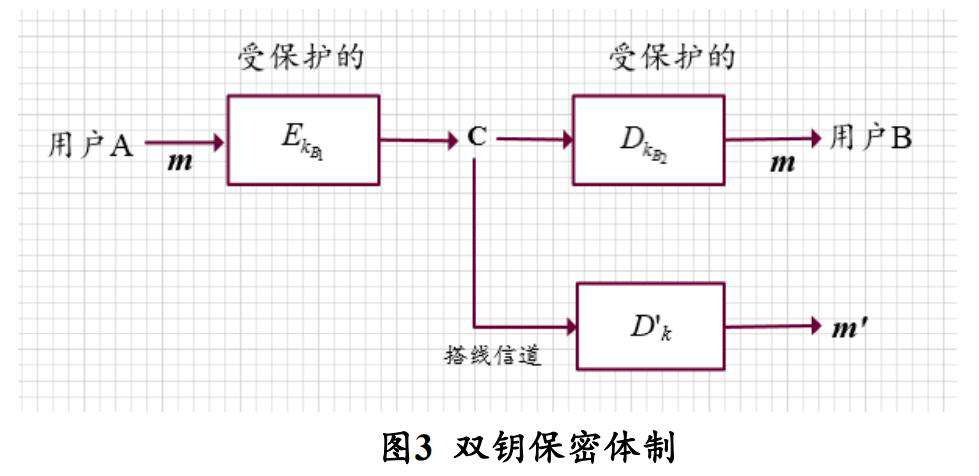
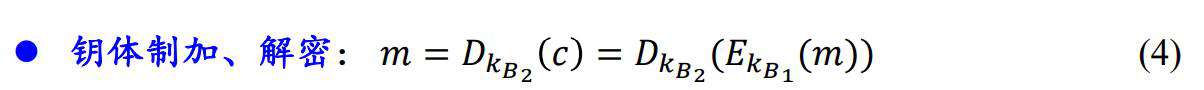
- 安全保障:从公开密钥Kb1和密文c不能推出B的私钥Kb2和明文。
- 由于任何人都可以使用B的公钥进行加密,所以密文c不具有认证性。
双钥认证体制

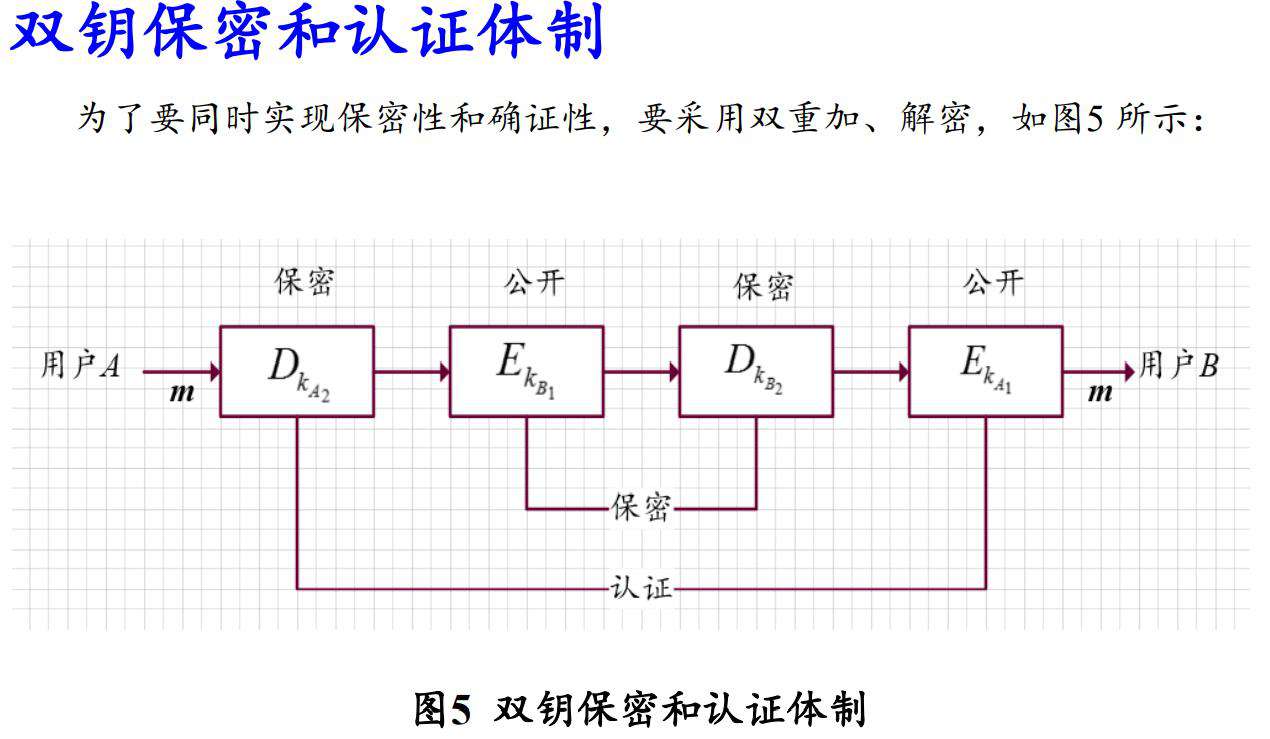
双钥保密和认证体制
所谓的双钥保密和认证体制就是说,假如A想发送消息给B,先用A的私钥对明文m进行加密,然后再使用B的公钥进行加密,这样就进行了两次加密过程,在解密的时候同样也是需要两次,先是使用B的私钥进行一次解密,然后使用A的公钥进行一次解密,这样B就可以获得需要的明文。

3:古典密码
代换密码
- 明文字母表A
- 密文字母表A’

- 加密变换
明文空间到密文空间的映射 - 判断有无数据拓展(明文字母表和密文字母表长度相同的时候)
明文长度 = 密文长度 没有数据拓展
明文长度 < 密文长度 有拓展
明文长度 > 密文长度 明文数据被压缩
再保密通信中需要拓展,认证系统中需要压缩,因为压缩是不可逆的,拓展存在很多种情况,所以拓展可以用来保密,压缩是唯一的,所以压缩可以用来进行认证。 - 什么是分组密码和流密码?

- 什么是单表代换和多表代换?
加解密使用同一个固定的代换表进行,我们称之为单表代换,例如经典的凯撒密码。
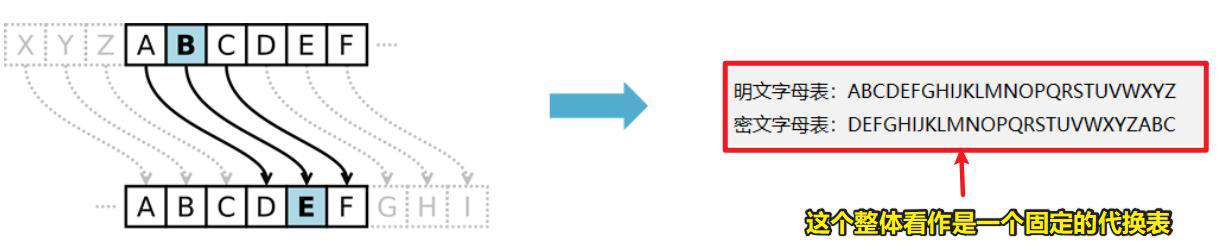
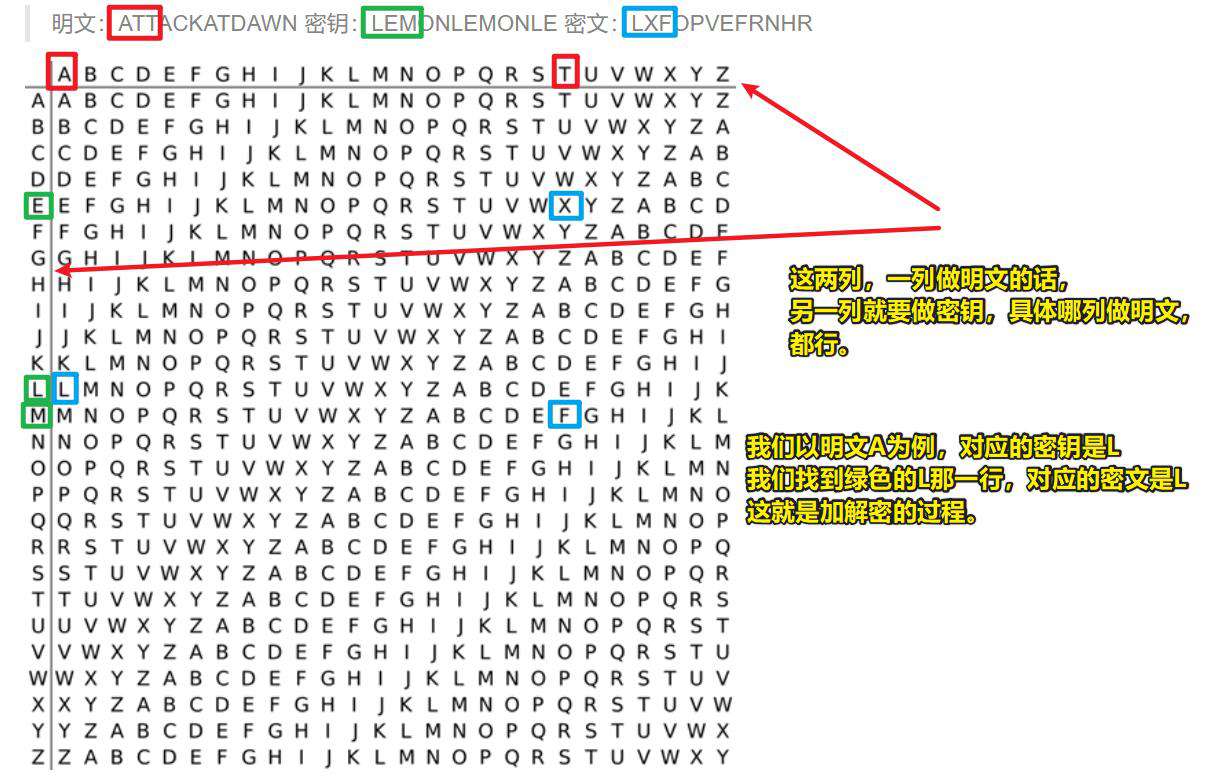
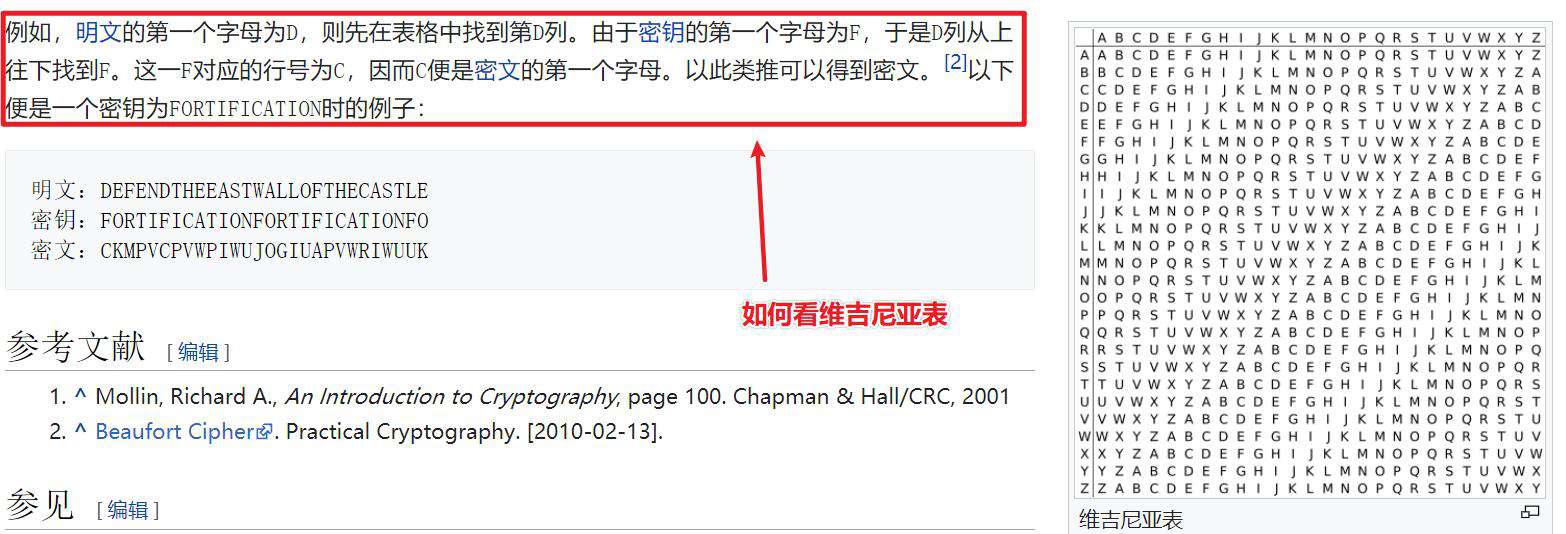
加解密使用一个以上的代换表进行代换,我们称之为多表代换,例如经典的维吉尼亚密码。具体选用哪个代换表进行,是根据密钥来的。
参考文献-密码学导论
单字母代换密码
移位代换密码

乘数密码

加密过程举例:

这里涉及到求逆元的操作,因此,可以使用拓展欧几里得的方法去求逆元。
- 在线求逆元的方式
www.wolframalpha.com/
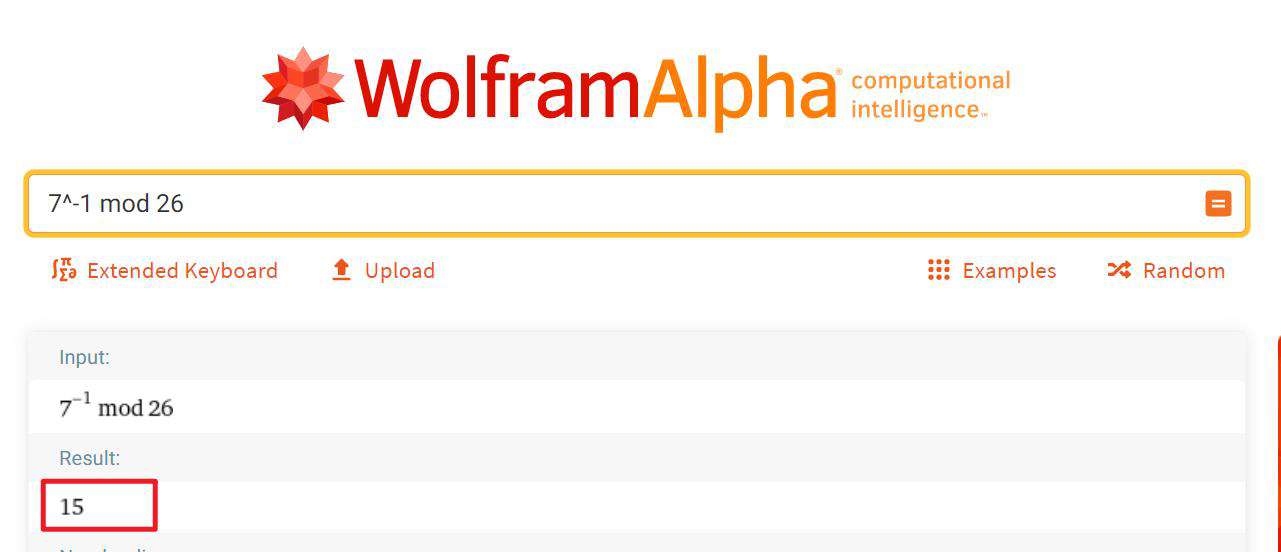
- 手动求逆元
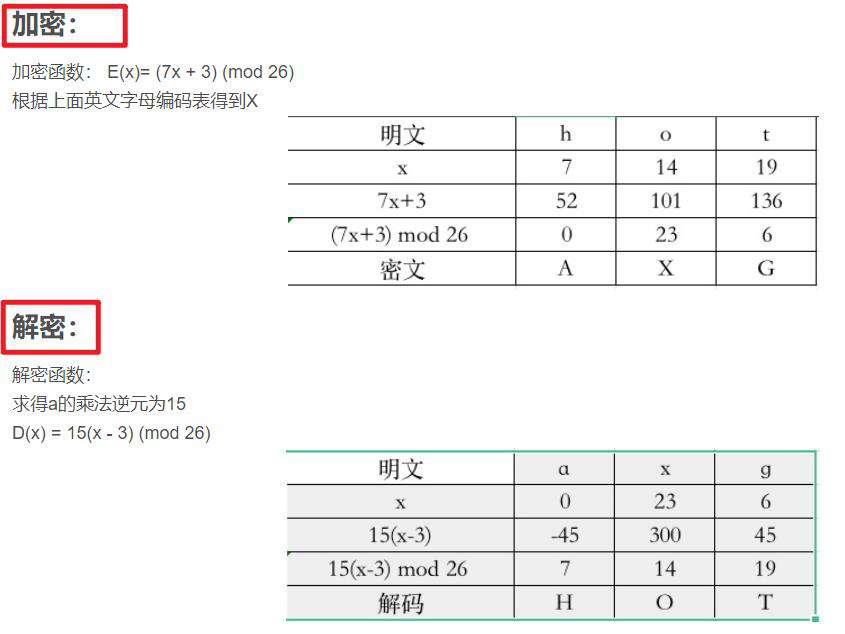
仿射密码
参考文献:仿射密码的加密与解密
首先看定义:

- 加密函数
- 解密函数
- 密钥指的是哪个?
- 限制条件
- 加解密实例分析,内容来自上面的参考文献
多项式代换密码

密钥短语密码

维吉尼亚密码

博福特密码
博福特密码几乎和维吉尼亚密码如出一辙,也是看维吉尼亚的那个加解密表,但是就是看法不同。具体看法如下图所示:
滚动密钥密码

弗纳姆密码
弗纳姆密码首先将明文字母转换为其对应的ASCII码5位的,然后与密钥进行异或运算(相同为0,相异为1)。

- 弗纳姆密码的加解密函数与相关例题

希尔密码
- 关于希尔密码的基本知识

- 希尔密码的加密过程

- 希尔密码的解密过程

4:初等密码分析
密码分析学
- 密码分析在外交、军事、公安、商业等方面都具有重要作用,也是研究历史、考古、古语言学和古乐理论的重要手段之一。
- 密码分析之所以能够破译密码,最根本的是依赖于明文中的多余度。
破译密码的方法
-
穷举破译法(也叫强力法)
-
分析法(有确定性和统计性两类)
- 确定分析法:如已知密文或者明文密文对,用数学关系式表示出所求未知量(密钥)
- 统计分析法:密码破译者对截收的密文进行统计分析,总结出其间的统计规律,并与明文的统计规律进行对照比较,从中提取出明文和密文之间的对应或变换信息。
密码可能经受不同水平的攻击

无条件安全
- 对密码体制的任何攻击,都不优于对明文的完全盲目的猜测,这样的密码体制就称为无条件安全的。
- 一次一密的加密方式容易实现无条件安全性。因为密钥实时更新,所以以往得到的任何明文密文对,对于破译新的密文没有任何的帮助,只能做完全盲目的猜测。
计算安全
- 对密码体制的任何攻击,虽然可能优于完全盲目的猜测,但超出了计算者的计算能力。这是最高级别的计算安全。
- 对密码体制的任何攻击,虽然可能没有超出攻击者的计算能力,但所付出的代价远远大于破译成功所得到的利益。这是第二级别的计算安全。
- 可能没有超出攻击者的能力,但是破译成功所需要的时间远远大于明文本身的有效期限。这也是第二级别的计算安全。
密码分析——破译实例
- 珍珠港事件
- 中途岛海战
- 冲绳岛战役
- 山本五十六之死
- 日本商船的毁灭
- 德国潜艇指挥部密码的破译
- 瑞典人破译德国外交和军事密码
- 海湾战争
- 苏联8.19事件
- RSA-129破译
- RSA-155破译
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!