题目描述

原题链接：二叉搜索树迭代器

实现一个二叉搜索树迭代器类 BSTIterator，表示一个按中序遍历二叉搜索树（BST）的迭代器，需包含 hasNext() 方法（返回下一个结点的值）、hasNext()方法（返回是否已遍历完整棵树）。

示例

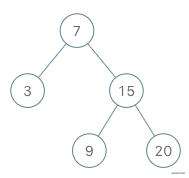
对于这棵树使用二叉搜索树迭代器应按如下返回：

BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // 返回 3
bSTIterator.next();    // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 20
bSTIterator.hasNext(); // 返回 False

进阶要求：next() 和 hasNext() 操作均摊时间复杂度为 O(1) ，并使用 O(h) 内存。其中 h 是树的高度。

解答

既然是二叉搜索树就必然离不开中序遍历，一般有递归和非递归的实现方式，其中中序遍历的递归实现相对简单：

function inorderTraversal(root){
    if(root.left) inorderTraversal(root.left)
    console.log(root.val) // 在这里操作结点
    if(root.right) inorderTraversal(root.right)
}

如果使用递归遍历的方式可以在 BSTIterator 的构造函数里先遍历一遍整棵树，将所有节点保存在一个队列中，调用 next() 方法时出队一个节点并返回它的 val 值，调用 hasNext() 方法只需要返回队列是否为空即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 */
const BSTIterator = function(root) {
    this.queue = []
    const inorderTraversal = (root) => {
        if(root.left) inorderTraversal(root.left)
        this.queue.push(root)
        if(root.right) inorderTraversal(root.right)
    }
    inorderTraversal(root)
};

/**
 * @return {number}
 */
BSTIterator.prototype.next = function() {
    return this.queue.shift().val
};

/**
 * @return {boolean}
 */
BSTIterator.prototype.hasNext = function() {
    return !!this.queue.length
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * var obj = new BSTIterator(root)
 * var param_1 = obj.next()
 * var param_2 = obj.hasNext()
 */

复杂度分析：这种解法用一个队列保存了所有结点，所以空间复杂度是 O(n)，next() 方法和 hasNext() 方法的时间复杂度均为 O(1)。

如果采用非递归的方式去遍历这棵树，就不需要在构造函数里遍历完整棵树。非递归实现方法如下：

function inorderTraversal(root){
    const stack = [];
    let cur = root
    while(cur){
        stack.push(cur)
        cur = cur.left
    }
    while(stack.length){
        const node = stack.pop()
        console.log(node.val) // 在这里操作结点
        cur = node.right
        while(cur){
            stack.push(cur)
            cur = cur.left
        }
    }
}

在本题中，若采用非递归的方式去遍历，仅需使用一个栈保存少量的结点即可：

var BSTIterator = function(root) {
    this.stack = []
    var cur = root
    while(cur){
        this.stack.push(cur)
        cur = cur.left
    }
};
BSTIterator.prototype.next = function() {
    var node = this.stack.pop()
    if(node.right){
        var cur = node.right
         while(cur){
            this.stack.push(cur)
            cur = cur.left
        }
    }
    return node.val
};
BSTIterator.prototype.hasNext = function() {
    return !!this.stack.length
};

复杂度分析：仅采用一个栈保存了数量最大为树高的结点，故空间复杂度为 O(h)，next() 方法和 hasNext() 方法的时间复杂度均为 O(1)。