二叉搜索树（二，前序遍历、中序遍历、后序遍历）

我们先来知道什么是前中后序遍历？然后思考下面两个问题

问题：

• 遍历就遍历，咋还有前中后呢？
• 为什么要有前中后序遍历？有啥用呢？

什么是前中后序遍历？

前序遍历：先访问根节点，再一次递归访问左右子树。

中序遍历：先递归访问左子树（以及里面的所有子树），再访问根节点，再递归访问右子树（里面的所有子树）。

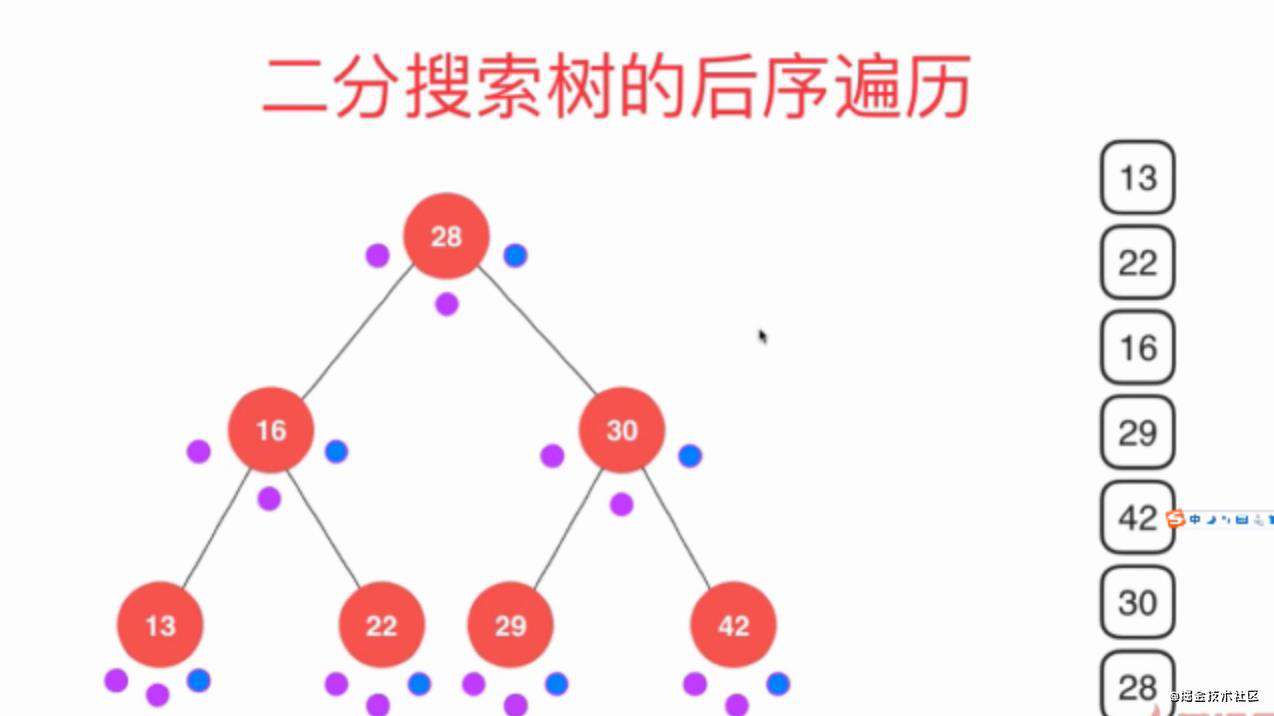
后序遍历：先递归访问左右子树，再访问根节点。 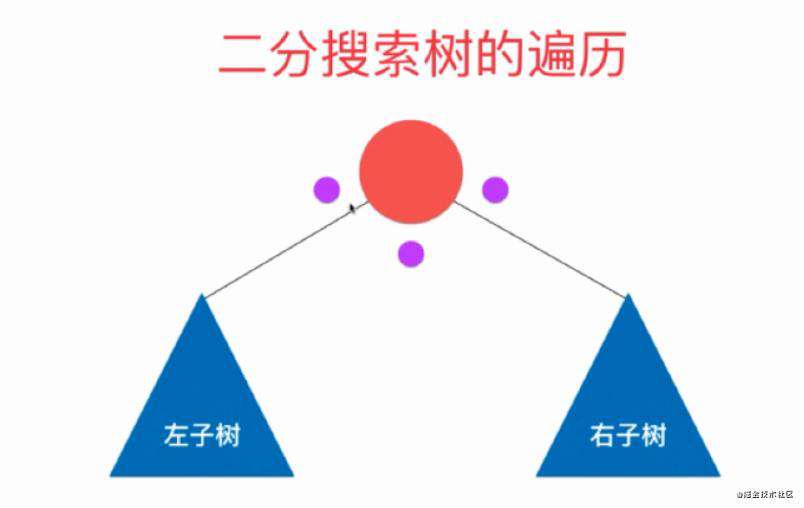上图中的三个点，从左到右分别代表着，前序、中序、后序。

还是不太明了，我们再来具体看看：

前序遍历打印的顺序：

• 先去查找28，然后打印出28
• 再去查找left 16，然后打印出16
• 再查找left 13，然后打印出13

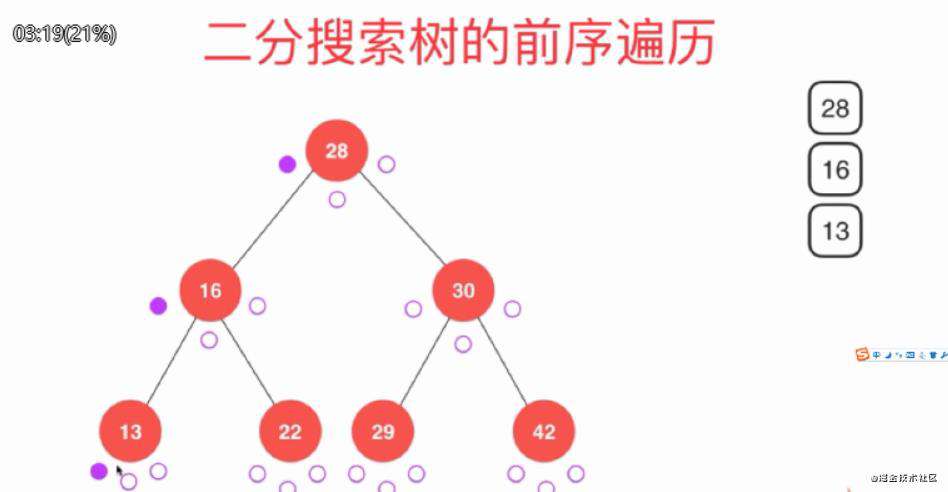
• 此时13为最下层，就没有left了。
• 然后会回到中间位置和right位置，因为我们是前序遍历，这两个位置我们什么都不做
• 然后回到16这个节点，发现有right节点，打印出22的前序位置
• 接下来循环，回到28访问28的右子树30。访问30的前序位置。打印出30。
• 然后访问30的左子树，打印出29，发现29没有节点。返回到30。
• 然后访问30的右子树，打印出42。

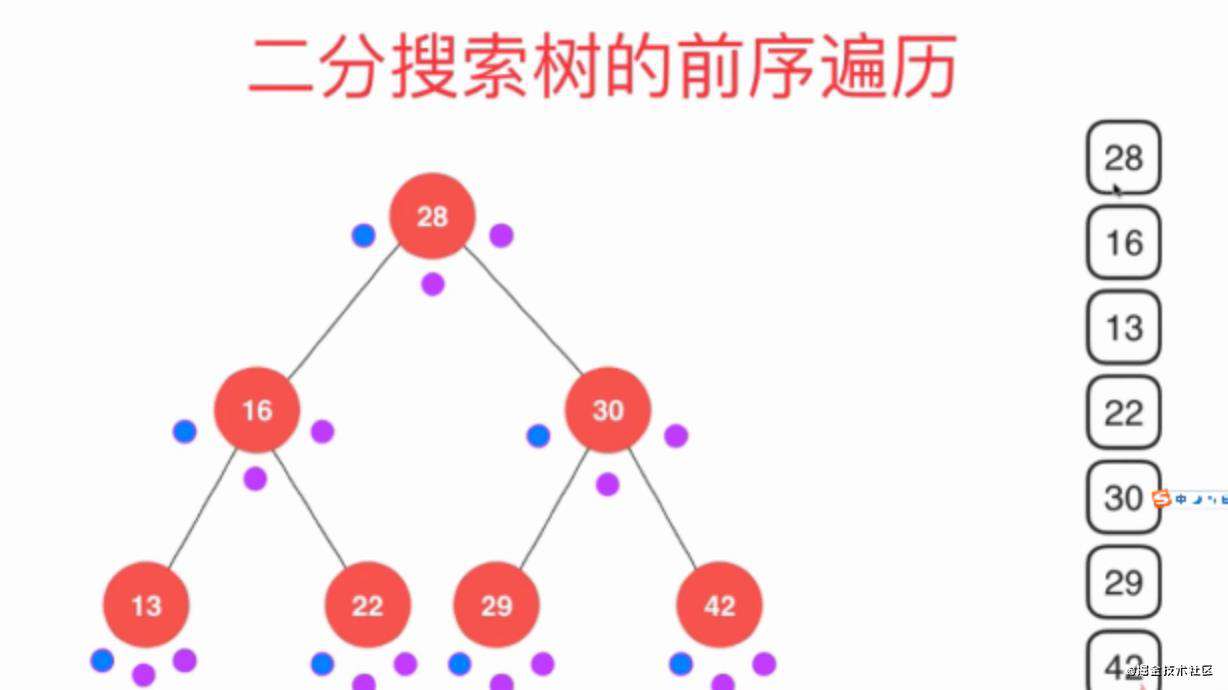
中序遍历打印顺序：

• 先进行28前序的位置，不打印，然后到16的前序位置不打印，之后到13的前序位置不打印。
• 然后回来到13的中序位置，打印出13，然后到13的后续位置不打印。
• 回到了16的中序位置打印出16，然后访问16的右子树。
• 到达22的前序位置，不打印，然后达到22的中序位置，打印出22。
• 然后到达22的后续位置，不打印，回到16的后序位置，不打印。
• 回到28的中序位置，打印出28。回到28的后续位置，不打印。
• 然后访问28的右子树，30前序位置不打印，访问29前序位置不打印。
• 然后访问29中序位置，打印出29，然后达到29后序位置，不打印。
• 回到30中序位置，打印出30，然后访问30的右子树，42的前序位置不打印。
• 42的中序位置，打印出42，然后访问42的后序位置，不打印，访问30的后序位置不打印，最后访问28的后序位置不打印，至此结束。

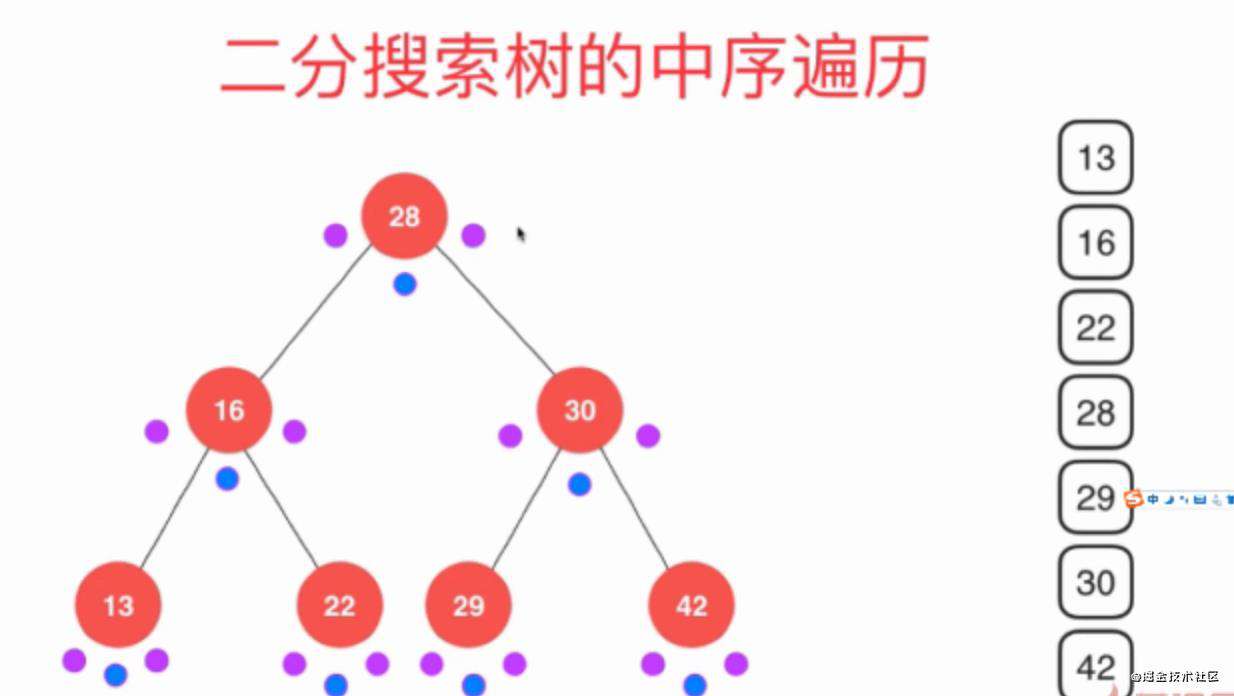
后序遍历打印顺序：

• 28前序，进入28左子树，16前序进入16左子树，13的前序中序不打印，后序打印出13。
• 返回到16中序进入到右子树，22前中不打印，后序打印出22。
• 返回到16后序，打印16。返回到28中序不打印，进入到28的右子树。
• 达到30的前序，进入到30的左子树，然后访问29前中序不打印，29后序打印出29。
• 返回到30中序，进入到30右子树，42前中不打印，后序打印出42。
• 返回到30后序，打印出30。
• 返回到28后序，打印出28。至此结束。

代码实现：

前序遍历：

function _preOrder(node) {
    if (node !== null) {
        console.log(node.key)
        this._preOrder(node.left)
        this._preOrder(node.right)
    }
}
let node = {
    key: 28,
    left: {
        key: 16,
        left: { key: 13, left: null, right: null },
        right: { key: 22, left: null, right: null }
    },
    right: {
        key: 30,
        left: { key: 29, left: null, right: null },
        right: { key: 42, left: null, right: null }
    }
}
console.log(_preOrder(node))
// 28 16 13 22 30 29 42

中序遍历：

function _inOrder(node) {
    if (node !== null) {
        this._inOrder(node.left)
        console.log(node.key)
        this._inOrder(node.right)
    }
}
let node = {
    key: 28,
    left: {
        key: 16,
        left: { key: 13, left: null, right: null },
        right: { key: 22, left: null, right: null }
    },
    right: {
        key: 30,
        left: { key: 29, left: null, right: null },
        right: { key: 42, left: null, right: null }
    }
}
console.log(_inOrder(nnode))
// 13 16 22 28 29 30 42

后序遍历：

function  _postOrder(node) {
    if (node !== null) {
        this._postOrder(node.left)
        this._postOrder(node.right)
        console.log(node.key)
    }
}
let node = {
    key: 28,
    left: {
        key: 16,
        left: { key: 13, left: null, right: null },
        right: { key: 22, left: null, right: null }
    },
    right: {
        key: 30,
        left: { key: 29, left: null, right: null },
        right: { key: 42, left: null, right: null }
    }
}
console.log(_postOrder(node))
// 13 22 16 29 42 30 28

结合上一篇文章的代码：

// 以node为根节点的二叉搜索树，插入节点（key，value）
// 返回插入新节点后的二叉搜索树
class Node {
    key
    value
    left
    right
    root = null
    count = 0
    constructor(key, value) {
        this.key = key
        this.value = value
        this.left = this.right = null
    }
    size() {
        return this.count;
    }
    isEmpty() {
        return this.count === 0;
    }
    preOrder() {
        this._preOrder(this.root)
    }
    inOrder() {
        this._inOrder(this.root)
    }
    postOrder() {
        this._postOrder(this.root)
    }
    // 前序遍历
    // 以node为根的二叉搜索树进行前序遍历
    _preOrder(node) {
        if (node !== null) {
            console.log(node.key)
            this._preOrder(node.left)
            this._preOrder(node.right)
        }
    }
    // 中序遍历
    // 以node为根的二叉搜索树进行中序遍历
    _inOrder(node) {
        if (node !== null) {
            this._inOrder(node.left)
            console.log(node.key)
            this._inOrder(node.right)
        }
    }
    // 后序遍历
    // 以node为根的二叉搜索树进行后序遍历
    _postOrder(node) {
        if (node !== null) {
            this._postOrder(node.left)
            this._postOrder(node.right)
            console.log(node.key)
        }
    }
}
// 数据结构是这样的
/*
    可能需要 插入/查找 到某个key对应的位置
*/
let node = {
    key: 28,
    left: {
        key: 16,
        left: { key: 13, left: null, right: null },
        right: { key: 22, left: null, right: null }
    },
    right: {
        key: 30,
        left: { key: 29, left: null, right: null },
        right: { key: 42, left: null, right: null }
    }
}

总结

我们同分析了那么久最后发现不过几行代码。

接下来会分析二叉搜索树的深度优先遍历和广度优先遍历。