一、题目描述：

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

原题链接 ? 455. 分发饼干

示例 1:

输入: g = [1,3,2], s = [2,1]
输出: 2
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,3,2。
虽然你有两块小饼干，由于他们的尺寸是1和2，能让胃口值分别是1和2的孩子满足。
所以你应该输出2。

示例 1:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

注意:

• 1 <= g.length <= 3 * 104
• 0 <= s.length <= 3 * 104
• 1 <= g[i], s[j] <= 231 - 1

二、思路分析：

思路：排序+贪心

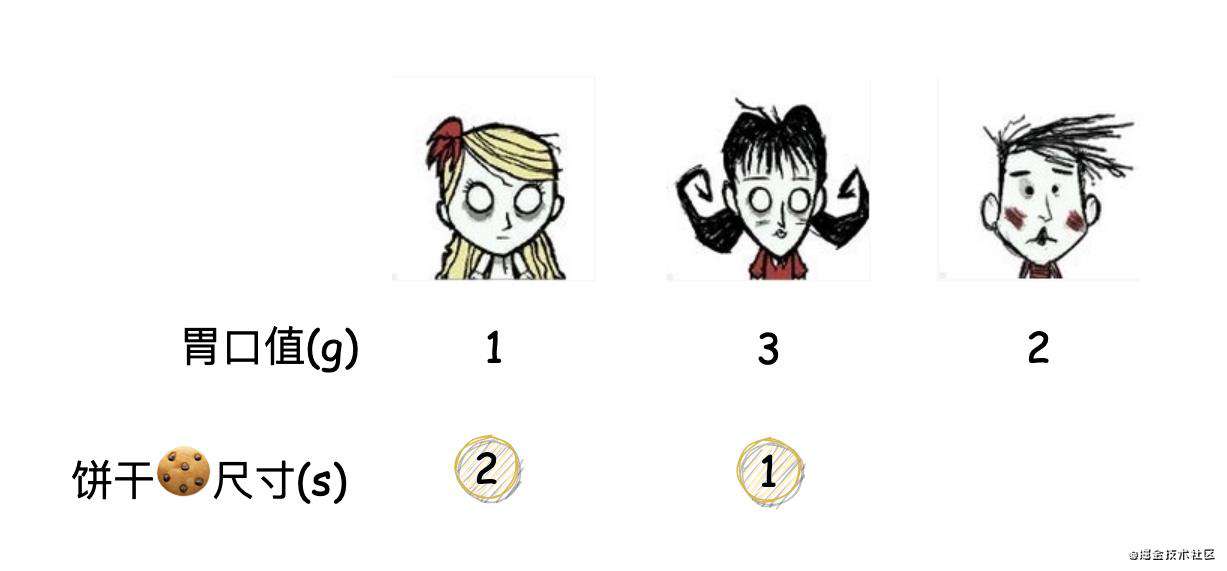
g = [1,3,2], s = [2,1]

1. 先分别给孩子的胃口值和饼干尺寸进行从小到大的排序

   排序完后g和s分别为：g = [1,2,3], s = [1,2]

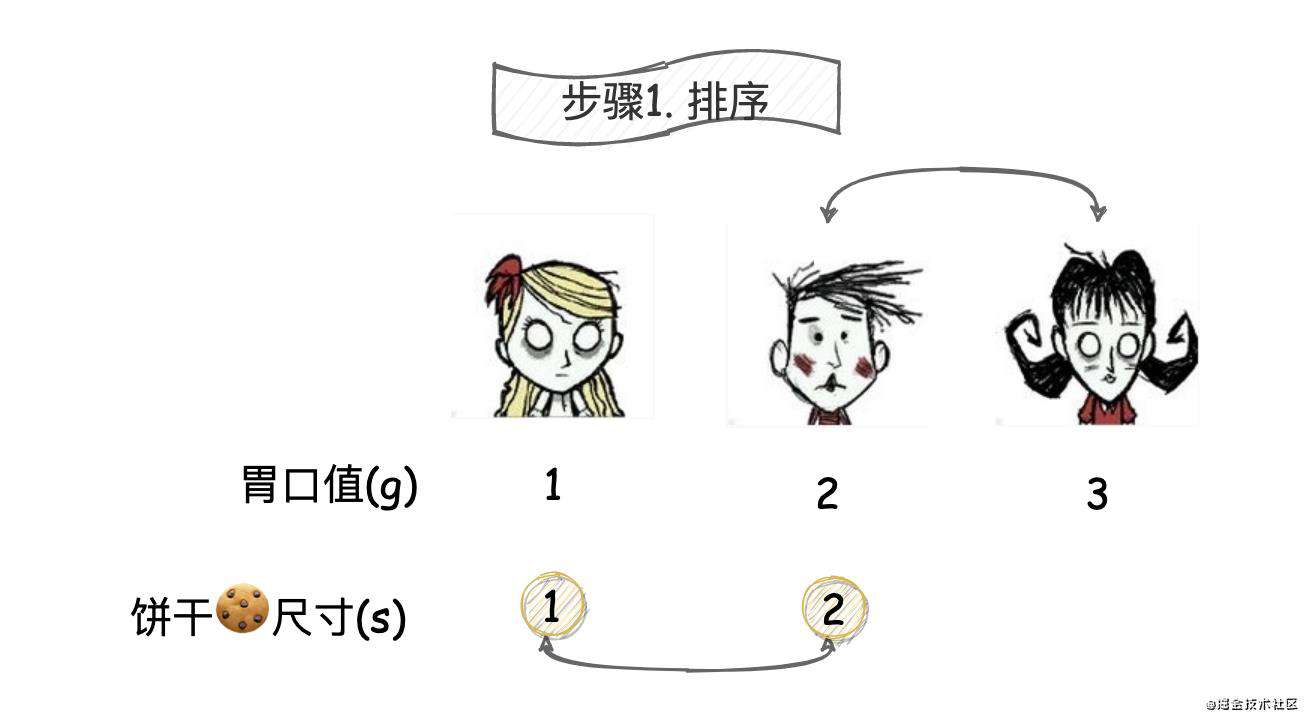
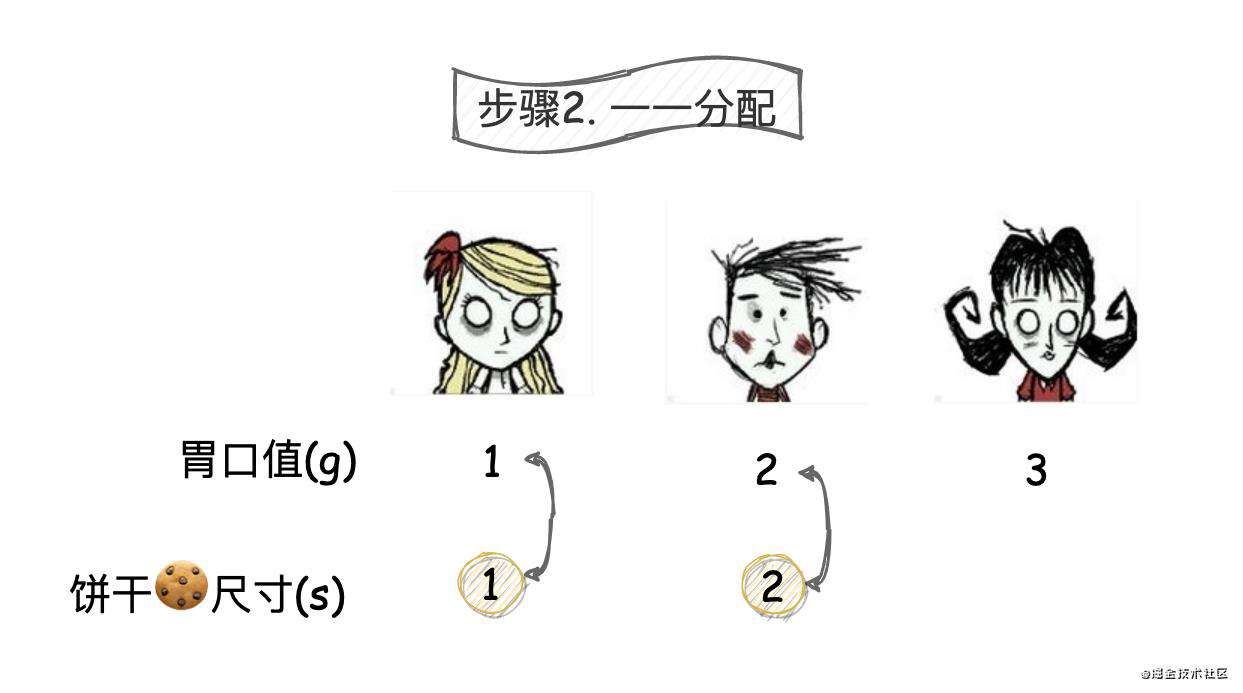
2. 循环饼干尺寸s，将饼干一一分配给孩子。

   • 设置index为孩子的索引，初始值为0。
   • 循环s时，拿当前饼干尺寸s[i]和孩子胃口值g[index]比较，如果s[i]>g[index]，那么满足了一个孩子，index++。否则，进行下一个循环。
   • 循环结束后index就是满足孩子的数值。

三、完整代码：

function findContentg(g, s) {
  g = g.sort((n1, n2) => n1 - n2)
  s = s.sort((n1, n2) => n1 - n2)
  let index = 0
  s.forEach((cookie, i) => {
    if (cookie >= g[index]) {
      index++
    }
  })
  return index
}

复杂度分析

• 时间复杂度： O(mlogm+nlogn)，其中 m 和 n 分别是数组 g 和 s 的长度。对两个数组排序的时间复杂度是 O(mlogm+nlogn)，遍历数组的时间复杂度是 O(n)，因此总时间复杂度是 O(mlogm+nlogn)。

四、总结：

分饼干问题的本质解法是贪心问题。如果遇到贪心问题首先想到的是要先排序再求解。

——

本文正在参与「掘金 2021 春招闯关活动」, 点击查看 活动详情