函数式编程

函数式编程是和面向对象编程（Object-oriented programming）以及过程式编程（Procedural programming）并列的编程范式。

范畴论

• 范畴论是函数式编程的起源。
• 范畴论（Category Theory）是数学中的一个抽象分支，能够形式化诸如集合论（set theory）、类型论（type theory）、群论（group theory）以及逻辑学（logic）等数学分支中的一些概念。

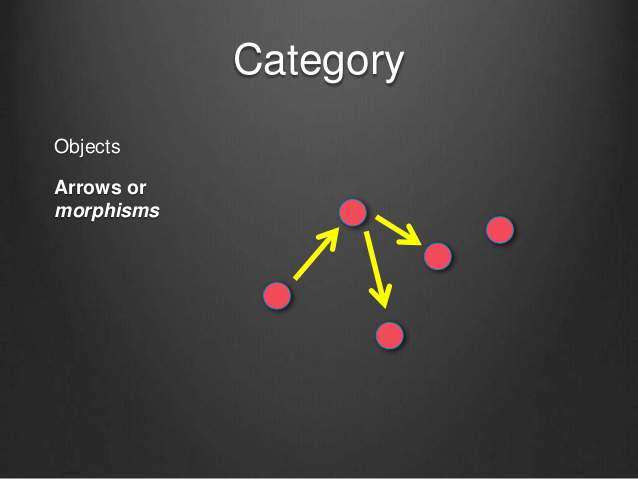
• 范畴是一组对象及其关系的集合，这些对象之间的关系（称为态射，morphisms）在组合（composition ）和结合性（associativity）方面表现良好。上图中，各个点与它们之间的箭头，就构成一个范畴。同一个范畴的所有成员（对象），就是不同状态的“变形”（transformation），箭头表示范畴成员之间的关系，正式名称叫做“态射”（morphism）。
• 集合范畴由集合和它们之间的关系（映射）组成；群范畴由群和它们之间的关系（群同态）组成；拓扑空间范畴由拓扑空间和它们之间的关系（连续映射）组成。在函数式编程中，成员（对象）就是数据类型，例如 String、Boolean、Number 和 Object 等等；“态射”就是标准的、普通的纯函数。
• 本质上，函数式编程只是范畴论的运算方法，跟数理逻辑、微积分、行列式是同一类东西，都是数学方法。它是一种数学运算，理论上通过函数，就可以从范畴的一个成员，算出其他成员，因此函数式编程要求函数必须是纯函数。

纯函数

// 不纯的
let minimum = 21

let checkAge = function(age) {
  return age >= minimum
}


// 纯的
let checkAge = function(age) {
  let minimum = 21
  return age >= minimum
}

副作用

副作用是在计算结果的过程中，系统状态的一种变化，或者与外部世界进行的可观察的交互。

副作用可能包含，但不限于：

• 更改文件系统
• 往数据库插入记录
• 发送一个 http 请求
• 可变数据
• 打印/log
• 获取用户输入
• DOM查询
• 访问系统状态

概括来讲，只要是跟函数外部环境发生的交互就都是副作用。

数学中的函数

纯函数就是数学中的函数：

• 函数是两种数值之间的关系：输入和输出。
• 每一个输入值返回且只返回一个输出值，即一一映射。
• 不同的输入可以有相同的输出。

纯函数的好处

可缓存性

纯函数总能够根据输入来做缓存，实现缓存的一种典型方式是 memoize 技术。

const memoize = function(f) {
  const cache = {}

  return function(...args) {
    const arg_str = JSON.stringify(args)
    cache[arg_str] = cache[arg_str] || f.apply(f, args)
    return cache[arg_str]
  }
}

const squareNumber = memoize(x => x * x)

squareNumber(4); // => 16

squareNumber(4); // => 16  从缓存中读取输入值为 4 的结果

可移值性

纯函数的依赖很明确，纯函数的所有依赖必须通过参数传递，从函数签名我们就可以推断出纯函数的作用。

纯函数和环境无关，可以在任何地方运行，可移植性可以意味着把函数序列化（serializing）并通过 socket 发送。也可以意味着代码能够在 web workers 中运行。

可测试性

纯函数让测试更加容易。我们不需要伪造一个“真实的”环境，或者每一次测试之前都要配置、之后都要断言状态（assert the state）。只需简单地给函数一个输入，然后断言输出就好了。

柯里化（curry）

偏函数/局部应用（partial application）

偏函数是指固定一个函数的一个或多个参数，然后产生另一个更小元的函数，也就是将一个 n 元函数转换成一个 n - x 元函数。

// 生成偏函数的工厂
const partial = (f, ...args) => (...moreArgs) => f(...args, ...moreArgs)
const rightPartial = (f, ...args) => (...moreArgs) => f(...moreArgs, ...args)

const add = (a, b, c) => a + b + c

// 固定参数 1 和 2，返回一个单参数函数
const fiveThree = partial(add, 1, 2) // 等价于 add.bind(null, 1, 2)

fiveThree(3) // => 6

柯里化

柯里化是将一个多参数函数转换成多个嵌套单参数函数，也就是将一个 n 元函数转换成 n 个嵌套的一元函数。也就是把 f(a, b, c) 转换成 f(a)(b)(c)。

const add = (a, b, c) => a + b + c

// 柯里化之后
// const curryAdd = a => b => c => a + b + c
const curryAdd = function(a) {
    return function(b) {
        return function(c) {
            return a + b + c
        }
    }
}

add(1, 2, 3) === curryAdd(1)(2)(3) === 6

// 柯里化工厂函数， curry 函数也允许一次传递多个参数
const curry = fn => {
    return judge = (...args) => args.length === fn.length
        ? fn(...args)
    	: (...moreArgs) => judge(...args, ...moreArgs)
}

const add = (a, b, c) => a + b + c

const curryAdd = curry(add)

add(1, 2, 3) // => 6
curryAdd(1, 2, 3) // => 6
curryAdd(1, 2)(3) // => 6
curryAdd(1)(2, 3) // => 6
curryAdd(1)(2)(3) // => 6

反柯里化

• 函数柯里化，是固定部分参数，返回一个接受剩余参数的函数，也称部分计算函数，目的是为了缩小适用范围，创建一个针对性更强的函数。
• 反柯里化函数，从字面将，意义和用法跟函数柯里化正好相反，扩大适用范围，创建一个应用范围更广的函数。使本来只有特定对象才适用的方法，扩展到更多的对象。

const unCurring = function(fn) {
    return function(...args) {
        const obj = args.shift()
        return fn.apply(obj, args)
    }
}

const push = unCurring(Array.prototype.push)
// 对象也能 push
const obj = {}
push(obj, 'one', 'two') // => {0: 'one', 1: 'two', length: 2}

组合（compose）

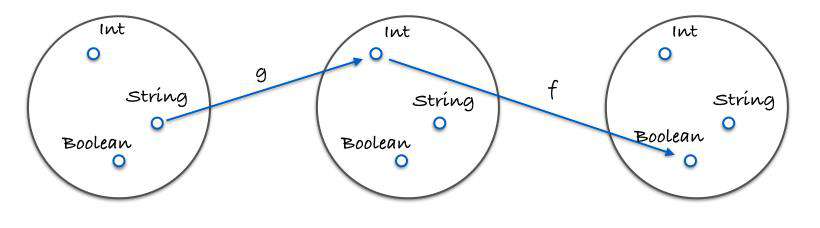
如果一个值要经过多个函数，才能变成另外一个值，为了解决函数嵌套（洋葱式代码h(g(f(x)))）就可以把所有中间步骤合并成一个函数，这叫做函数组合（compose）。

const compose = (f, g) => (x => f(g(x)))

// first:: [a] -> a
const first = arr => arr[0]
// reverse:: [a] -> [a]
const reverse = arr => arr.reverse()

const last = compose(first, reverse)

last([1, 2, 3, 4]) // => 4

// 通用 compose 函数
const compose = (...funcs) => {
    const identity = x => x
    return funcs.reduce((a, b) => (...args) => a(b(...args)), identity)
}

compose 函数特点：

• 参数是多个函数，返回值是一个“组合函数”；
• 组合函数内的所有函数从右至左依次执行，从右向左执行更加能够反映数学上的含义；
• 组合函数内除了第一个执行函数的参数是多元的，其他函数的参数都是接收上一个函数的返回值。一般来说，约定每个函数都为一元函数。

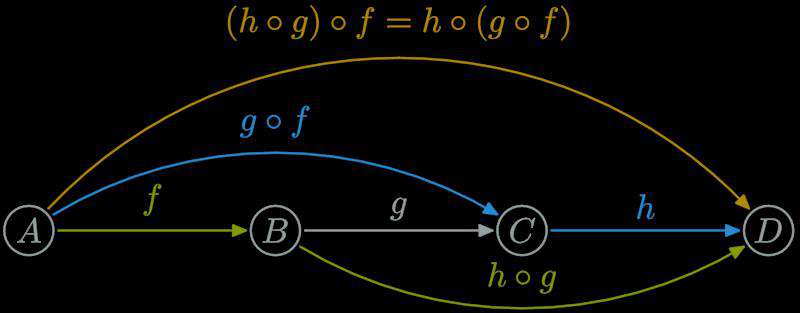
结合律：

/**
* 以下三种方式效果一致
*/
compose(f, compose(g, h))
compose(compose(f, g), h)
compose(f, g, h)

pipe（管道）

• compose 函数的数据流是从右至左，pipe 函数的数据流是从左至右（gulp、rxjs）。

// rxjs 是主流的基于函数式编程的响应式编程库
import { from } from 'rxjs'
import { map, filter, catchError } from 'rxjs/operators'

from([1, 2, 3]).pipe(
  filter(x => x % 2 === 0), // 过滤出偶数
  map(x => x * x), // 求平方
  catchError(err => console.error(err)) // 错误处理
).subscribe(console.log)

pipe(...operations: OperatorFunction<any, any>[]): Observable<any> {
  if (operations.length === 0) {
    return this as any;
  }
  if (operations.length == 1) {
     return operation[0];
  }

  return operations.reduce((prev, fn) => fn(prev), this);
}

函数式编程有三大特性：声明式的，不可变的，没有副作用的。函数式的程序就是通过管道把数据在一系列纯函数之间传递的程序。

范畴与容器

我们可以把范畴想象成是一个容器，里面包含两样东西：值（value）、值的变形关系（函数）。

const Container = function(x) {
    this.__value = x
}

// of 函数用于生成新的容器
Container.of = function(x) {
    return new Container(x)
}

函数不仅可以用于同一个范畴之间值的转换，还可以用于将一个范畴转成另一个范畴。这就涉及到了函子（Functor）。

实现了 of 方法的 functor 称为 pointed functor。

函子（Functor）

函子是函数式编程里面最重要的数据类型，也是基本的运算单位和功能单位。

它首先是一种范畴，也就是说，是一个容器，包含了值和变形关系。比较特殊的是，它的变形关系可以依次作用于每一个值，将当前容器变形成另一个容器。

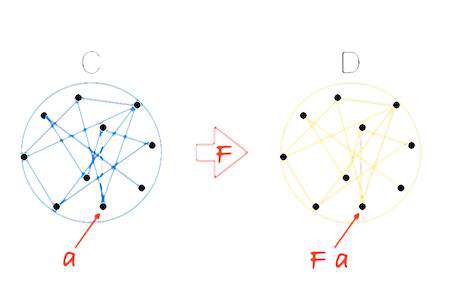
• 函子的标志就是容器具有map方法。该方法将容器里面的每一个值，映射到另一个容器。

class Functor {
    constructor(x) {
        this.__value = x
    }

    map(f: Function): Functor {
        return Functor.of(f(this.__value))
    }
}

Functor.of = function(x) {
    return new Functor(x)
}

• 上面代码中，Functor 是一个函子，它的 map 方法接受函数 f 作为 参数，然后返回一个新的函子，里面包含的值是被 f 处理过的 （f(this.val)）。
• 函数式编程里面的运算，都是通过函子完成，即运算不直接针对值，而是针对这个值的容器----函子。函子本身具有对外接口（map方法），各种函数就是运算符，通过接口接入容器，引发容器里面的值的变形。Container 里的值传递给 map 函数之后，就可以任我们操作；操作结束后，为了防止意外再把它放回它所属的 Container。这样做的结果是，我们能连续地调用 map，运行任何我们想运行的函数。一直调用 map，就是组合（compose）。

Maybe 函子

函子通过 map 接受各种函数，处理容器内部的值。容器内部的值可能是一个空值（比如null），而外部函数未必有处理空值的机制，这时很可能就会出错。

Functor.of(null).map(x => x.toString()) // => TypeError

Maybe 函子就是用来处理这种情况的。Maybe 的 map 函数会先进行空值检查，然后才调用传进来的函数，这样处理空值就不会出错了。

class Maybe extends Functor {
    isNullOrUndefined() {
        return this.__value === null || this.__value === undefined
    }

    map(f) {
        return this.isNullOrUndefined() ? Maybe.of(null) : Maybe.of(f(this.__value))
    }
}

Maybe.of = function(x) {
    return new Maybe(x)
}

Maybe.of(null).map(x => x.toString()) // => Maybe(null)

Either 函子

Either 函子是一种更纯粹的处理错误的方式，Either 函子内部有两个值：左值（Left）和右值（Right）。右值是正常情况下使用的值，左值是右值不存在时使用的默认值。

// Left
class Left extends Functor {
    map(f) {
        return this
    }
}
Left.of = function(x) {
  	return new Left(x);
}

// Right
class Right extends Functor {
    map(f) {
        return new Right.of(f(this.__value))
    }
}
Right.of = function(x) {
  	return new Right(x)
}

const getAge = user => user.age ? Right.of(user.age) : Left.of("ERROR!")

getAge({name: 'stark', age: '21'})
    .map(age => 'Age is ' + age) //=> Right('Age is 21')

getAge({name: 'stark'})
    .map(age => 'Age is ' + age); //=> Left('ERROR!')

• Left 可以让调用链中任意一环的错误立刻返回到调用链的尾 部，这给我们错误处理带来了很大的方便，再也不用一层又一 层的 try/catch。

IO 函子

从localStorage 中取值的函数会产生副作用，但是把它包裹在另个函数里延迟执行可以使它看起来像一个纯函数。

const getFromStorage = function(key) {
    return function() {
        return localStorage[key]
    }
}

IO 函子的 __value 是一个函数，它把不纯的操作（比如 IO、网络请求）包裹到一个函数内，目的是延迟执行这个非纯动作。

class IO {
    constructor(f: Function) {
        this.__value = f
    }

    map(f) {
        return IO.of(compose(f, this.__value))
    }
}

IO.of = function(x) {
    return new IO(function() {
        return x
    })
}

AP 函子（application functor）

函子里面包含的值，完全可能是函数。我们可以想象这样一种情况，一个函子的值是数值，另一个函子的值是函数。

function addTwo(x) {
  return x + 2
}

const A = Functor.of(2)
const B = Functor.of(addTwo)

我们想让函子 B 内部的函数，可以使用函子 A 内部的值进行运算。这时就需要用到 ap 函子。

ap 函子是实现了 实现了 ap 方法的 pointed functor ，赋予不同 functor 可以相互应用（apply）的能力。

class Ap extends Functor {
  	ap(F: Functor) {
    	return Ap.of(this.__value(F.__value))
  	}
}

Ap.of = function(x) {
    return new Ap(x)
}

Ap.of(addTwo).ap(Functor.of(2)) // => Ap(4)

ap 函子的意义在于，对于那些多参数的函数，就可以从多个容器之中取值，实现函子的链式操作。

function add(x) {
    return function(y) {
        return x + y
    }
}

Ap.of(add).ap(Functor(2)).ap(Functor(3)) // => Ap(5)

Monad 函子

函子是一个容器，可以包含任何值。函子之中再包含一个函子，也是完全合法的。但是，这样就会出现多层嵌套的函子。

Functor.of(Functor.of(Functor.of(6)))

上面的函子如果要取出内部的值，就要连续取三次 this.__value。这个时候需要 monad 函子。

monad 是可以变扁（flatten）的 pointed functor 。

class Monad extends Functor {
  	join() {
    	return this.__value
  	}

  	flatMap(f) {
    	return this.map(f).join()
  	}
}

Monad 函子的作用是，总是返回一个单层的函子。它有一个 flatMap 方法，与map方法作用相同，唯一的区别是如果生成了一个嵌套函子， flatMap 会取出后者内部的值，保证返回的永远是一个单层的容器，不会出现嵌套的情况，即嵌套的函子会被铺平（flatten）。

应用

• Rxjs （函数响应式编程）
• lodash 、underscore
• redux (状态机和函数式编程)

store -> container
state -> __value
action -> Functor
reducer -> map
middleware -> IO functor(异步)

总结

• 函数式编程不是万能的，它和 OOP 一样，只是一种编程范式而已。OOP 降低复杂度是靠良好的封装、继承、多态以及接口定义；函数式编程是通过纯函数以及它们的组合、柯里化、Functor 等技术来降低系统复杂度。
• 很多实际应用中是很难用函数式编程去表示的，只要记住函数对于外部状态的依赖是造成系统复杂性大大提高的主要原因，尽量让函数尽可能纯净就行。

参考资料

• 函数式编程入门教程
• 函数式编程指北
• 函数式编程术语