译者：sea_ljf

原文链接

很多（上层）数据结构，如 Map、Set 等，它们的基础数据结构都（可以）是 Tree。同时，在数据库中快速搜索（元素）用到了树。HTML 的 DOM 节点也通过树来表示对应的层次结构。以上仅仅是树的一少部分例子。在这篇文章中，我们将探讨不同类型的树，如二叉树、二叉搜索树以及如何实现它们。

在上一篇文章中，我们探讨了数据结构：图，它是树一般化的情况。让我们开始学习树吧！

本篇是以下教程的一部分（译者注：如果大家觉得还不错，我会翻译整个系列的文章）:

初学者应该了解的数据结构与算法（DSA）

1. 算法的时间复杂性与大 O 符号
2. 每个程序员应该知道的八种时间复杂度
3. 初学者应该了解的数据结构：Array、HashMap 与 List
4. 初学者应该了解的数据结构： Graph
5. 初学者应该了解的数据结构：Tree ? 即本文
6. 自平衡二叉搜索树
7. 附录 I：递归算法分析

树的基本概念

在树中，每个节点可有零个或多个子节点，每个节点都包含一个值。和图一样，节点之间的连接被称为边。树是图的一种，但并不是所有图都是树（只有无环无向图才是树）。

这种数据类型之所以被称为树，是因为它长得很像一棵（倒置的）树 ?。它从根节点出发，它的子节点是它的分支，没有任何子节点的节点就是树的叶子（即叶节点）。

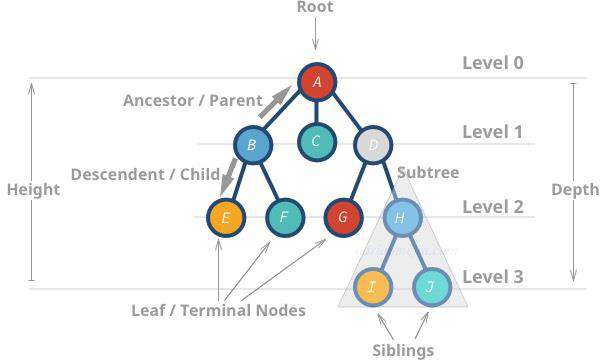
以下是树的一些属性：

• 最顶层的节点被称为根（root）节点（译者注：即没有任何父节点的节点）。
• 没有任何子节点的节点被称为叶节点（leaf node）或者终端节点（terminal node）。
• 树的度（Height）是最深的叶节点与根节点之间的距离（即边的数量）。
  • A 的度是 3。
  • I 的度是 0（译者注：子树也是树，I 的度是指 I 为根节点的子树的度）。
• 深度（Depth）或者层次（level）是节点与根节点的距离。
  • H 的层次是 2。
  • B 的层次是 1。

树的简单实现

正如此前所见，树的节点有一个值，且存有它每一个子节点的引用。

以下是节点的例子：

class TreeNode {
  constructor(value) {
    this.value = value;
    this.descendents = [];
  }
}

我们可以创建一棵树，它有三个叶节点：

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendents
abe.descendents.push(homer);
homer.descendents.push(bart, lisa, maggie);

这样就完成啦，我们有了一棵树！

![](p0.ssl.qhimg.com/t01516921af… ""Simpson tree data structure"")

节点 abe 是根节点，而节点 bart、lisa 和 maggie 则是这棵树的 叶节点。注意，树的节点的子节点可以是任意数量的，无论是 0 个、1 个、3 个或是多个均可。

二叉树

树的节点可以有 0 个或多个子节点。然而，当一棵树（的所有节点）最多只能有两个子节点时，这样的树被称为二叉树。

二叉树是树中最常见的形式之一，它应用广泛，如：

• Maps
• Sets
• 数据库
• 优先队列
• 在 LDAP（Lightweight Directory Access Protocol）中查找相应信息。
• 在 XML/HTML 文件中，使用文档对象模型（DOM）接口进行搜索。

完满二叉树、完全二叉树、完美二叉树

取决于二叉树节点的组织方式，一棵二叉树可以是完满二叉树、完全二叉树或完美二叉树。

• 完满二叉树（Full binary tree）：除去叶节点，每个节点都有两个子节点。
• 完全二叉树（Complete binary tree）：除了最深一层之外，其余所有层的节点都必须有两个子节点（译者注：其实还需要最深一层的节点均集中在左边，即左对齐）。
• 完美二叉树（Perfect binary tree）：满足完全二叉树性质，树的叶子节点均在最后一层（也就是形成了一个完美的三角形）。

（译者注：国内外的定义是不同的，此处根据原文与查找的资料，作了一定的修改，用的是国外的标准）

下图是上述概念的例子：

![](p0.ssl.qhimg.com/t01b0d1575b… ""Full vs. Complete vs. Perfect Binary Tree"")

完满二叉树、完全二叉树与完美二叉树并不总是互斥的：

• 完美二叉树必然是完满二叉树和完全二叉树。
  • 完美的二叉树正好有 2 的 k 次方 减 1 个节点，其中 k 是树的最深一层（从1开始）。.
• 完全二叉树并不总是完满二叉树。
  • 正如上面的完全二叉树例子，最右侧的灰色节点是它父子点仅有的一个子节点。如果移除掉它，这棵树就既是完全二叉树，也是完满二叉树。（译者注：其实有了那个灰色节点的话，这颗树不能算是完全二叉树的，因为完满二叉树需要左对齐）
• 完满二叉树并不一定是完全二叉树与完美二叉树。

二叉搜索树 (BST)

二叉搜索树（Binary Search Tree，简写为：BST）是二叉树的特定应用。BST 的每个节点如二叉树一样，最多只能有两个子节点。然而，BST 左子节点的值必须小于父节点的值，而右子节点的值则必须大于父节点的值。

强调一下：一些 BST 并不允许重复值的节点被添加到树中，如若允许，那么重复值的节点将作为右子节点。有些二叉搜索树的实现，会记录起重复的情况（这也是接下来我们需要实现的）。

一起来实现二叉搜索树吧！

BST 的实现

BST 的实现与上文树的实现相像，然而有两点不同：

• 节点最多只能拥有两个子节点。
• 节点的值满足以下关系：左子节点 < 父节点 < 右子节点。

以下是树节点的实现，与之前树的实现类似，但会为左右子节点添加 getter 与 setter。请注意，实例中会保存父节点的引用，当添加新的子节点时，将更新（子节点中）父节点的引用。

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
  constructor(value) {
    this.value = value;
    this.descendents = [];
    this.parent = null;
    //译者注：原文并没有以下两个属性，但不加上去话下文的实现会报错
    this.newNode.isParentLeftChild = false;
    this.meta = {};  
  }
  get left() {
    return this.descendents[LEFT];
  }
  set left(node) {
    this.descendents[LEFT] = node;
    if (node) {
      node.parent = this;
    }
  }
  get right() {
    return this.descendents[RIGHT];
  }
  set right(node) {
    this.descendents[RIGHT] = node;
    if (node) {
      node.parent = this;
    }
  }
}

OK，现在已经可以添加左右子节点。接下来将编写 BST 类，使其满足 左子节点 < 父节点 < 右子节点。

class BinarySearchTree {
  constructor() {
    this.root = null;
    this.size = 0;
  }
  add(value) { /* ... */ }
  find(value) { /* ... */ }
  remove(value) { /* ... */ }
  getMax() { /* ... */ }
  getMin() { /* ... */ }
}

下面先编写插入新节点相关的的代码。

BST 节点的插入

要将一个新的节点插入到二叉搜索树中，我们需要以下三步：

1. 如果树中没有任何节点，第一个节点当成为根节点。
2. （将新插入节点的值）与树中的根节点或树节点进行对比，如果值 更大，则放至右子树（进行下一次对比），反之放到左子树（进行对比） 。如果值一样，则说明被重复添加，可增加重复节点的计数。
3. 重复第二点操作，直至找到空位插入新节点。

让我们通过以下例子来说明，树中将依次插入30、40、10、15、12、50：

![](p0.ssl.qhimg.com/t011df4b16e… ""Inserting nodes on a Binary Search Tree (BST)"")

代码实现如下：

add(value) {
  const newNode = new TreeNode(value);
  if (this.root) {
    const { found, parent } = this.findNodeAndParent(value);
    if (found) { // duplicated: value already exist on the tree
      found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
    } else if (value < parent.value) {
      parent.left = newNode;
      //译者注：原文并没有这行代码，但不加上去的话下文实现会报错
      newNode.isParentLeftChild = true;
    } else {
      parent.right = newNode;
    }
  } else {
    this.root = newNode;
  }
  this.size += 1;
  return newNode;
}

我们使用了名为 findNodeAndParent 的辅助函数。如果（与新插入节点值相同的）节点已存在于树中，则将节点统计重复的计数器加一。看看这个辅助函数该如何实现：

findNodeAndParent(value) {
  let node = this.root;
  let parent;
  while (node) {
    if (node.value === value) {
      break;
    }
    parent = node;
    node = ( value >= node.value) ? node.right : node.left;
  }
  return { found: node, parent };
}

findNodeAndParent 沿着树的结构搜索值。它从根节点出发，往左还是往右搜索取决于节点的值。如果已存在相同值的节点，函数返回找到的节点（即相同值的节点）与它的父节点。如果没有相同值的节点，则返回最后找到的节点（即将变为新插入节点父节点的节点）。

BST 节点的删除

我们已经知道如何（在二叉搜索树中）插入与查找值，现在将实现删除操作。这比插入而言稍微麻烦一点，让我们用下面的例子进行说明：

删除叶节点（即没有任何子节点的节点）

    30                             30
 /     \         remove(12)     /     \
10      40       --------->    10      40
  \    /  \                      \    /  \
  15  35   50                    15  35   50
  /
12*

只需要删除父节点（即节点 #15）中保存着的 节点 #12 的引用即可。

删除有一个子节点的节点

    30                              30
 /     \         remove(10)      /     \
10*     40       --------->     15      40
  \    /  \                            /  \
  15  35   50                         35   50

在这种情况中，我们将父节点 #30 中保存着的子节点 #10 的引用，替换为子节点的子节点 #15 的引用。

删除有两个子节点的节点

   30                              30
 /     \         remove(40)      /     \
15      40*      --------->     15      50
       /  \                            /
      35   50                         35

待删除的节点 #40 有两个子节点（#35 与 #50）。我们将待删除节点替换为节点 #50。待删除的左子节点 #35 将在原位不动，但它的父节点已被替换。

另一个删除节点 #40 的方式是：将左子节点 #35 移到节点 #40 的位置，右子节点位置保持不变。

    30
 /     \
15      35
          \
           50

两种形式都可以，这是因为它们都遵循了二叉搜索树的原则：左子节点 < 父节点 < 右子节点。

删除根节点

   30*                            50
 /     \       remove(30)      /     \
15      50     --------->     15      35
       /
      35

删除根节点与此前讨论的机制情况差不多。唯一的区别是需要更新二叉搜索树实例中根节点的引用。

以下的动画是上述操作的具体展示：

![](p0.ssl.qhimg.com/t01ae013251… ""Removing a node with 0, 1, 2 children from a binary search tree"")

在动画中，被移动的节点是左子节点或者左子树，右子节点或右子树位置保持不变。

关于删除节点，已经有了思路，让我们来实现它吧：

remove(value) {
  const nodeToRemove = this.find(value);
  if (!nodeToRemove) return false;
  // Combine left and right children into one subtree without nodeToRemove
  const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
  if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
    nodeToRemove.meta.multiplicity -= 1; // handle duplicated
  } else if (nodeToRemove === this.root) {
    // Replace (root) node to delete with the combined subtree.
    this.root = nodeToRemoveChildren;
    this.root.parent = null; // clearing up old parent
  } else {
    const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
    const { parent } = nodeToRemove; // get parent
    // Replace node to delete with the combined subtree.
    parent[side] = nodeToRemoveChildren;
  }
  this.size -= 1;
  return true;
}

以下是实现中一些要注意的地方：

• 首先，搜索待删除的节点是否存在。如果不存在，返回 false。
• 如果待删除的节点存在，则将它的左子树合并到右子树中，组合为一颗新子树。
• 替换待删除的节点为组合好的子树。

将左子树组合到右子树的函数如下：

combineLeftIntoRightSubtree(node) {
  if (node.right) {
    //译者注：原文是  getLeftmost，寻找左子树最大的节点，这肯定有问题，应该是找最小的节点才对
    const leftLeast = this.getLefLeast(node.right);  
    leftLeast.left = node.left;
    return node.right;
  }
  return node.left;
}

正如下面例子所示，我们想把节点 #30 删除，将待删除节点的左子树整合到右子树中，结果如下：

   30*                             40
 /     \                          /  \
10      40    combine(30)       35   50
  \    /  \   ----------->      /
  15  35   50                  10
                                \
                                 15

现在把新的子树的根节点作为整个二叉树的根节点，节点 #30 将不复存在！

二叉树的遍历

根据遍历的顺序，二叉树的遍历有若干种形式：中序遍历、先序遍历与后序遍历。同时，我们也可以使用在《初学者应该了解的数据结构： Graph》一文中学到的 DFS 或 BFS 来遍历整棵树。以下是具体的实现：

中序遍历（In-Order Traversal）

中序遍历访问节点的顺序是：左子节点、节点本身、右子节点。

* inOrderTraversal(node = this.root) {
    if (node.left) { yield* this.inOrderTraversal(node.left); }
    yield node;
    if (node.right) { yield* this.inOrderTraversal(node.right); }
  }

用以下这棵树作为例子：

         10
       /    \
      5      30
    /       /  \
   4       15   40
 /
3

中序遍历将按照以下顺序输出对应的值：3、4、5、10、15、30、40。也就是说，如果待遍历的树是一颗二叉搜索树，那输出值的顺序将是升序的。

后序遍历（Post-Order Traversal）

后序遍历访问节点的顺序是：左子节点、右子节点、节点本身。

* postOrderTraversal(node = this.root) {
    if (node.left) { yield* this.postOrderTraversal(node.left); }
    if (node.right) { yield* this.postOrderTraversal(node.right); }
    yield node;
  }

后序遍历将按照以下顺序输出对应的值：3、4、5、15、40、30、10。

先序遍历与 DFS（Pre-Order Traversal）

先序遍历访问节点的顺序是：节点本身、左子节点、右子节点。

* preOrderTraversal(node = this.root) {
    yield node;
    if (node.left) { yield* this.preOrderTraversal(node.left); }
    if (node.right) { yield* this.preOrderTraversal(node.right); }
  }

先序遍历将按照以下顺序输出对应的值：10、5、4、3、30、15、40。与深度优先搜索（DPS）的顺序是一致的。

广度优先搜索 (BFS)

树的 BFS 可以通过队列来实现：

* bfs() {
    const queue = new Queue();
    queue.add(this.root);
    while (!queue.isEmpty()) {
      const node = queue.remove();
      yield node;
      node.descendents.forEach(child => queue.add(child));
    }
  }

BFS 将按照以下顺序输出对应的值：10、5、30、4、15、40、3。

平衡树 vs. 非平衡树

目前，我们已经讨论了如何新增、删除与查找元素。然而，我们并未谈到（相关操作的）时间复杂度，先思考一下最坏的情况。

假设按升序添加数字：

![](p0.ssl.qhimg.com/t014b63aee4… ""Inserting values in ascending order in a Binary Search Tree"")

树的左侧没有任何节点！在这颗非平衡树（ Non-balanced Tree）中进行查找元素并不比使用链表所花的时间短，都是 O(n)。 ?

在非平衡树中查找元素，如同以逐页翻看的方式在字典中寻找一个单词。但如果树是平衡的，将类似于对半翻开字典，视乎该页的字母，选择左半部分或右半部分继续查找（对应的词）。

需要找到一种方式使树变得平衡！

如果树是平衡的，查找元素不在需要遍历全部元素，时间复杂度降为 O(log n)。让我们探讨一下平衡树的意义。

![](p0.ssl.qhimg.com/t01348a324b… ""Balanced vs unbalanced Tree"")

如果在非平衡树中寻找值为 7 的节点，就必须从节点 #1 往下直到节点 #7。然而在平衡树中，我们依次访问 #4、#6 后，下一个节点将到达 #7。随着树规模的增大，（非平衡树的）表现会越来越糟糕。如果树中有上百万个节点，查找一个不存在的元素需要上百万次访问，而平衡树中只要20次！这是天壤之别！

我们将在下一篇文章中通过自平衡树来解决这个问题。

总结

我们讨论了不少树的基础，以下是相关的总结：

• 树是一种数据结构，它的节点有 0 个或多个子节点。
• 树并不存在环，图才存在。
• 在二叉树中，每个节点最多只有两个子节点。
• 当一颗二叉树中，左子节点的值小于节点的值，而右子节点的值大于节点的值时，这颗树被称为二叉搜索树。
• 可以通过先序、后续和中序的方式访问一棵树。
• 在非平衡树中查找的时间复杂度是 O(n)。 ??
• 在平衡树中查找的时间复杂度是 O(log n)。 ?