最近看了《数据结构与算法-JavaScript描述》,是一本以JavaScript来实现一些常见数据结构的书,对于数据结构来说算是入门书,值得入手。
数据结构(本书):数组,列表,队列,链表,字典,散列,集合
算法(本书):排序算法,检索算法,高级算法
这本书只是介绍几种常用的数据结构和算法、
今天说排序。
对计算机中存储的数据执行的两种最常见操作是排序和检索,自从计算机产业伊始便是如 此。这也意味着排序和检索在计算机科学中是被研究得最多的操作。本书讨论的许多数据 结构,都对排序和查找算法进行了专门的设计,以使对其中的数据进行操作时更简洁高效。
基本排序
冒泡排序
之所以叫冒泡排序是因为使用这种排序算法排序时,数据值会像气泡一样从数组的一端漂 浮到另一端。假设正在将一组数字按照升序排列,较大的值会浮动到数组的右侧,而较小 的值则会浮动到数组的左侧。之所以会产生这种现象是因为算法会多次在数组中移动,比 较相邻的数据,当左侧值大于右侧值时将它们进行互换。
// 冒泡排序
var arr = [2,12,5,3,78,46,96,67,23]
function bubbleSort() {
for (var i = 0; i<arr.length-1;i++){
for (var j = 0; j<arr.length-1-i;j++){
if (arr[j]>=arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
console.log(bubbleSort(arr))
// [2, 3, 5, 12, 23, 46, 67, 78, 96]
选择排序
选择排序从数组的开头开始,将第一个元素和其他元 素进行比较。检查完所有元素后,最小的元素会被放到数组的第一个位置,然后算法会从 第二个位置继续。这个过程一直进行,当进行到数组的倒数第二个位置时,所有的数据便 完成了排序。
选择排序会用到嵌套循环。外循环从数组的第一个元素移动到倒数第二个元素;内循环从第 二个数组元素移动到最后一个元素,查找比当前外循环所指向的元素小的元素。每次内循环 迭代后,数组中最小的值都会被赋值到合适的位置.

function selectionSort(dataStore) {
var min;
var temp;
for (var outer = 0; outer <= dataStore.length-2; outer++) {
min = outer;
for (var inner = outer + 1;inner <= dataStore.length-1; inner++) {
if (dataStore[inner] < dataStore[min]) {
min = inner;
temp = dataStore[outer];
dataStore[outer] = dataStore[inner];
dataStore[inner] = temp;
}
}
}
return dataStore;
}
// console.log(selectionSort(arr))
// [2, 3, 5, 12, 23, 67, 46, 78, 96]
插入排序
插入排序有两个循环。外循环将数组元素挨个移动,而内循环则对外循环中选中的元素及 它后面的那个元素进行比较。如果外循环中选中的元素比内循环中选中的元素小,那么数 组元素会向右移动,为内循环中的这个元素腾出位置,就像之前介绍的姓氏卡片一样。

function insertionSort(dataStore) {
var temp, inner;
for (var outer = 0; outer <= dataStore.length - 1; outer++) {
temp = dataStore[outer];
inner = outer;
while (inner > 0 && (dataStore[inner - 1] >= temp)) {
dataStore[inner] = dataStore[inner - 1];
--inner;
}
dataStore[inner] = temp;
}
return dataStore;
}
console.log(insertionSort(arr))
// [2, 3, 5, 12, 23, 67, 46, 78, 96]
这三种在这本书中被介绍为基本排序,经过测试,10 000 个数字的测试结果与 1000 个数字的测试结果一致。选择排序和插入排序要比冒泡 排序快,插入排序是这三种算法中最快的。
高级排序
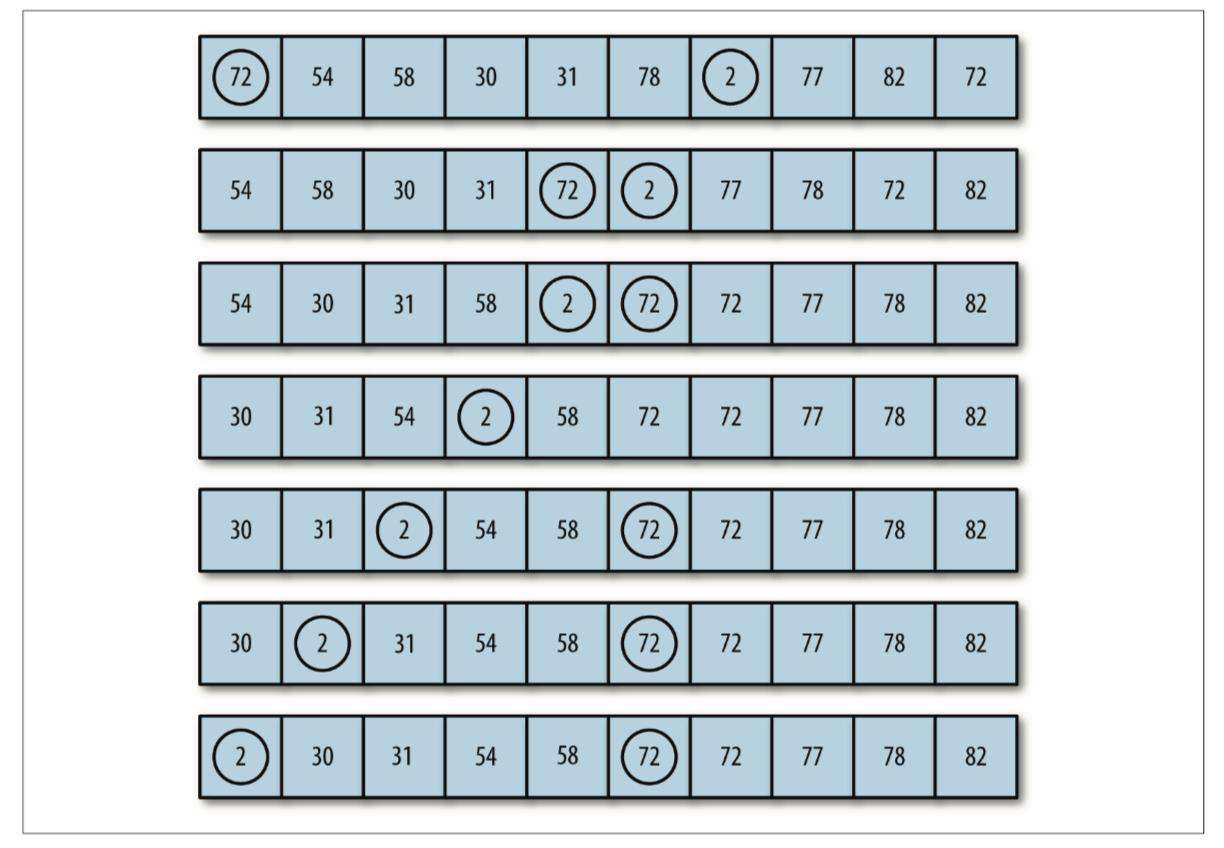
希尔排序
希尔排序的工作原理是,通过定义一个间隔序列来表示在排序过程中进行比较的元素之 间有多远的间隔。我们可以动态定义间隔序列,不过对于大部分的实际应用场景,算法 要用到的间隔序列可以提前定义好。
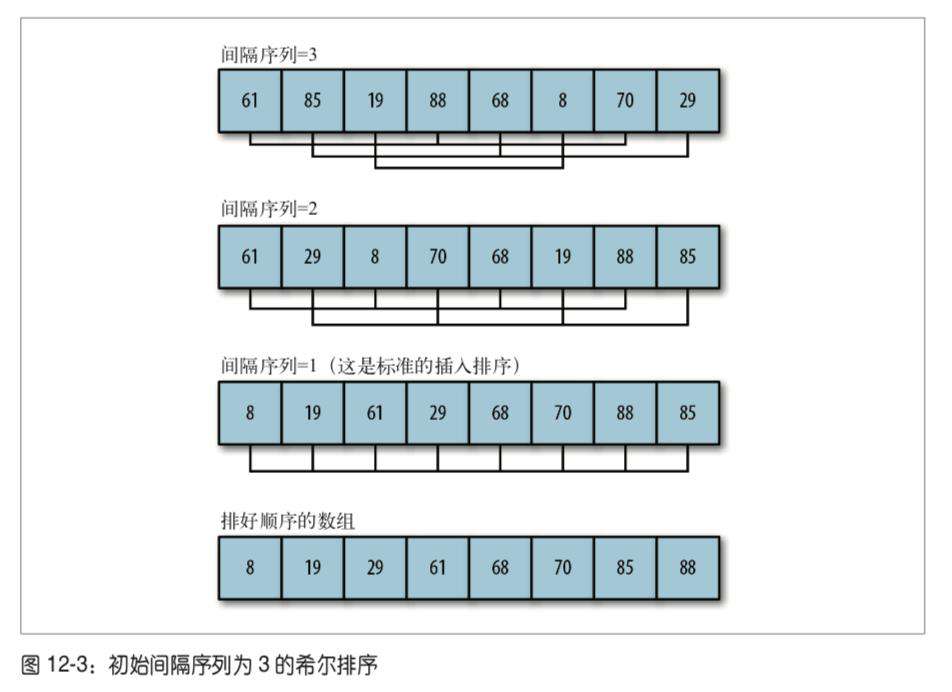
外循环控制间隔序列的移动。以5,3,1为例,算法在第一次处理数据集时,会检查所有间隔为 5 的元素。下一次遍历会检查所有间隔为 3 的元素。最后一次则会对间隔为 1 的元素,也 就是相邻元素执行标准插入排序。在开始做最后一次处理时,大部分元素都将在正确的位 置,算法就不必对很多元素进行交换。这就是希尔排序比插入排序更高效的地方。图 12-3 演示了如何使用间隔序列为 5, 3, 1 的希尔排序算法,对一个包含 10 个随机数字的数据集 合进行排序。
function shellsort1(dataStore) {
var N = dataStore.length;
var h = 1;
while (h < N/3) {
h = 3 * h + 1;
}
while (h >= 1) {
for (var i = h; i < N; i++) {
for (var j = i; j >= h && dataStore[j] < dataStore[j-h];
j -= h) {
var temp = dataStore[j];
dataStore[j] = dataStore[j-h];
dataStore[j-h] = temp;
}
}
h = (h-1)/3;
}
return dataStore
}
console.log(shellsort1(arr))
// [2, 3, 5, 12, 23, 67, 46, 78, 96]
归并排序
归并排序的命名来自它的实现原理:把一系列排好序的子序列合并成一个大的完整有序序 列。从理论上讲,这个算法很容易实现。我们需要两个排好序的子数组,然后通过比较数 据大小,先从最小的数据开始插入,最后合并得到第三个数组。然而,在实际情况中,归 并排序还有一些问题,当我们用这个算法对一个很大的数据集进行排序时,我们需要相当 大的空间来合并存储两个子数组。就现在来讲,内存不那么昂贵,空间不是问题,因此值 得我们去实现一下归并排序,比较它和其他排序算法的执行效率。
自顶向下的归并排序
归并排序会使用递归的算法来实现。
function mergeSort(arr){
// 设置终止的条件,
if (arr.length < 2) {
return arr;
}
//设立中间值
var middle = parseInt(arr.length / 2);
//第1个和middle个之间为左子列
var left = arr.slice(0, middle);
//第middle+1到最后为右子列
var right = arr.slice(middle);
if(left=="undefined"&&right=="undefined"){
return false;
}
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right){
var result = [];
while (left.length && right.length) {
if(left[0] <= right[0]){
//把left的左子树推出一个,然后push进result数组里
result.push(left.shift());
}else{
//把right的右子树推出一个,然后push进result数组里
result.push(right.shift());
}
}
//经过上面一次循环,只能左子列或右子列一个不为空,或者都为空
while (left.length){
result.push(left.shift());
}
while (right.length){
result.push(right.shift());
}
return result;
}
// 测试数据
var nums=[6,10,1,9,4,8,2,7,3,5];
console.log(mergeSort(nums));
自底向上的归并排序
递归的深度太深,使用一种非递归的方式。首先将数据集分解为一组只有一个元素的数组,然后通过创建一组左右子数组慢慢将它们合并起来, 每次合并都保存一部分排好序的数据,最后这个数组排序完全。
function mergeSort(arr){
if(arr.length<2){
return;
}
//设置子序列的大小
var step=1;
var left,right;
while(step<arr.length){
left=0;
right=step;
while(right+step<=arr.length){
mergeArrays(arr,left,left+step,right,right+step);
left=right+step;
right=left+step;
}
if(right<arr.length){
mergeArrays(arr,left,left+step,right,arr.length);
}
step*=2;
}
return arr;
}
//对左右序列进行排序
function mergeArrays(arr,startLeft,stopLeft,startRight,stopRight){
// 建立一个左、右数组
var rightArr=new Array(stopRight-startRight+1);
var leftArr=new Array(stopLeft-startLeft+1);
// 给右数组赋值
k=startRight;
for(var i=0;i<(rightArr.length-1);++i){
rightArr[i]=arr[k];
++k;
}
// 给左数组赋值
k=startLeft;
for(var i=0;i<(leftArr.length-1);++i){
leftArr[i]=arr[k];
++k;
}
//设置哨兵值,当左子列或右子列读取到最后一位时,即Infinity,可以让另一个剩下的列中的值直接插入到数组中
rightArr[rightArr.length-1]=Infinity;
leftArr[leftArr.length-1]=Infinity;
var m=0;
var n=0;
// 比较左子列和右子列第一个值的大小,小的先填入数组,接着再进行比较
for(var k=startLeft;k<stopRight;++k){
if(leftArr[m]<=rightArr[n]){
arr[k]=leftArr[m];
m++;
}
else{
arr[k]=rightArr[n];
n++;
}
}
}
// 测试数据
var nums=[6,10,1,9,4,8,2,7,3,5];
console.log(mergeSort(nums));
快速排序
快速排序是处理大数据集最快的排序算法之一。它是一种分而治之的算法,通过递归的方 式将数据依次分解为包含较小元素和较大元素的不同子序列。该算法不断重复这个步骤直 到所有数据都是有序的。
这个算法首先要在列表中选择一个元素作为基准值(pivot)。数据排序围绕基准值进行, 将列表中小于基准值的元素移到数组的底部,将大于基准值的元素移到数组的顶部。
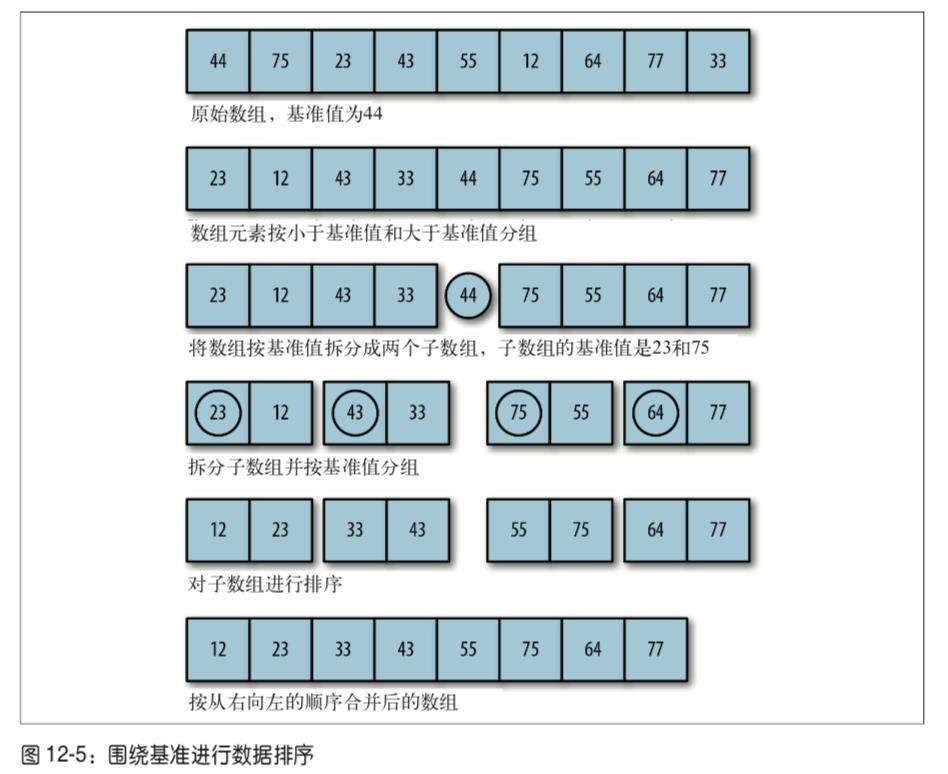
快速排序的算法如下:
(1) 选择一个基准元素,将列表分隔成两个子序列;
(2) 对列表重新排序,将所有小于基准值的元素放在基准值的前面,所有大于基准值的元
素放在基准值的后面;
(3) 分别对较小元素的子序列和较大元素的子序列重复步骤 1 和 2。
function qSort(list) {
if (list.length == 0) {
return [];
}
var lesser = [];
var greater = [];
var pivot = list[0];
for (var i = 1; i < list.length; i++) {
if (list[i] < pivot) {
lesser.push(list[i]);
} else {
greater.push(list[i]);
}
}
return qSort(lesser).concat(pivot, qSort(greater));
}
console.log(qSort(arr))
// [2, 3, 5, 12, 23, 67, 46, 78, 96]
常见问题FAQ
- 免费下载或者VIP会员专享资源能否直接商用?
- 本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。更多说明请参考 VIP介绍。
- 提示下载完但解压或打开不了?
- 找不到素材资源介绍文章里的示例图片?
- 模板不会安装或需要功能定制以及二次开发?






发表评论
还没有评论,快来抢沙发吧!