【Daily Interview】- 21 解数独

题目

分析

对数独规则不太清楚的读者可以看看这里：数独。

同之前的单词搜索和 N 皇后问题类似，数独的解题思路同样简单粗暴：

• 看看当前位置能不能填
• 如果可以则填入，继续判断下一个位置
• 如果遇到死路则退回来填入其他结果

而这也就是回溯算法的核心了，以数独为例，我们可以看看下面的流程图，方便理解回溯算法：

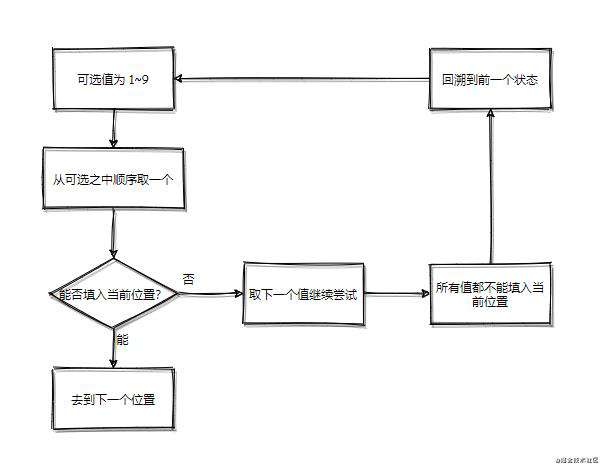
那么我们可以根据这个套路，完成代码的宏观架构：

var solveSudoku = function (board) {
  // 遍历棋盘
  for (let i = 0; i < 9; i++) {
    for (let j = 0; j < 9; j++) {
      // 如果当前格子不为 .，说明已经被下过，直接跳过即可
      if (board[i][j] !== ".") continue;
      for (let value = 1; value <= 9; value++) {
        if (canset()) {
          // 更新状态，进入下一步，回退状态
          board[i][j] = value;
          solveSudoku(board);
          board[i][j] = ".";
        }
      }
    }
  }
};

对于上述代码，不能忘的是考虑边界条件：

• 何时回退
  • 显然当当前格子所有值都不能填入的时候，就应该回退了，那么应该在遍历完 1~9 的可选值之后返回 false
• 何时结束
  • 整个棋盘都被填完的时候，这时说明解出答案，就可以结束了，这个时候应该返回 true

代码如下：

var solveSudoku = function (board) {
  // 遍历棋盘
  for (let i = 0; i < 9; i++) {
    for (let j = 0; j < 9; j++) {
      // 如果当前格子不为 .，说明已经被下过，直接跳过即可
      if (board[i][j] !== ".") continue;
      for (let value = 1; value <= 9; value++) {
        if (canSet()) {
          // 更新状态，进入下一步，回退状态
          board[i][j] = value;
+          if (solveSudoku(board)) return true;
          board[i][j] = ".";
        }
      }
+      return false;
    }
  }
+  return true;
};

接下来就是细节上的实现：如何判断当前格子是否能填入对应数字。

对于这个问题，我们理清规则其实不难：

• 当前行已经有的所有值都不能与 value 相等
• 当前列已经有的所有值都不能与 value 相等
• 当前 3 x 3 的九宫格内所已经有的所有值都不能与 value 相等

前二者比较简单，只需固定死 row 和 col 即可，而第三个，我们则需要首先找到当前遍历到的格子属于哪一块九宫格。

这里我们来看一个数独：

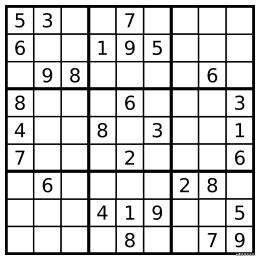
可以看到，9 个九宫格将整个 9 x 9 的棋盘分成了 9 块，那么我们完全可以忽略掉小格子，将其转化成 3 x 3 的棋盘。

const x = Math.floor(row / 3) * 3;
const y = Math.floor(col / 3) * 3;

这样就可以定位是具体的九宫格了。

综上，完善 canSet 代码：

const canSet = (board, row, col, value) => {
  const x = Math.floor(row / 3) * 3;
  const y = Math.floor(col / 3) * 3;
	
	// 九宫格内有数字与 value 相等
  for (let i = 0; i < 3; i++) {
    for (let j = 0; j < 3; j++) {
      if (board[x + i][y + j] === value) {
        return false;
      }
    }
  }

	// 行列有数字与 value 相等
  for (let i = 0; i < 9; i++) {
    if (board[row][i] === value || board[i][col] === value) {
      return false;
    }
  }

  return true;
};

结果如下：