【Daily Interview】- 16 遍历二叉树

题目

!! 题目来源：二叉树的前序遍历 - 力扣、二叉树的中序遍历 - 力扣、二叉树的后序遍历 - 力扣

分析

要解决今天的问题，首先要明白什么是前序遍历，什么是中序遍历，什么又是后序遍历。

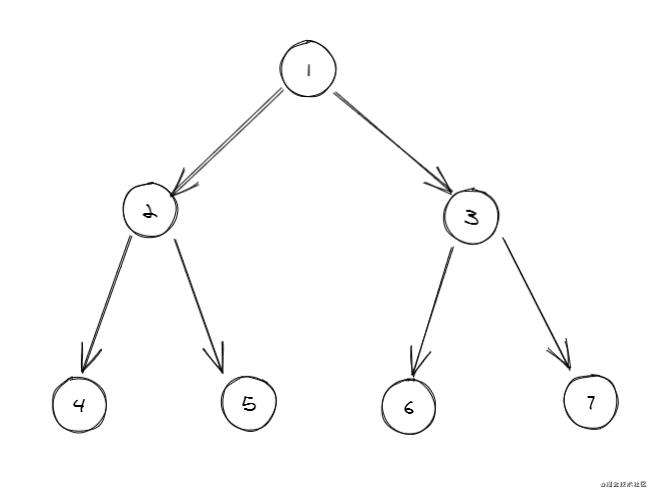
其实很简单，三者的区别在于遍历节点的顺序，我们以下面的二叉树为例：

三种遍历顺序分别如下：

• 前序遍历：根 → 左 → 右。上树遍历结果如下：[1, 2, 4, 5, 3, 6, 7]
• 中序遍历：左 → 根 → 右。上树遍历结果如下：[4, 2, 5, 1, 3, 6, 7]
• 后续遍历：左 → 右 → 根。上树遍历结果如下：[4, 5, 2, 3, 6, 7, 1]

那么要实现不同的遍历，我们只需要再不同的时候处理节点即可：

// 前序遍历
var preorderTraversal = function (root, ary = []) {
  if (root !== null) {
    ary.push(root.val);
    preorderTraversal(root.left, ary);
    preorderTraversal(root.right, ary);
  }
  return ary;
};

// 中序遍历
var inorderTraversal = function(root) {
  if (root !== null) {
    preorderTraversal(root.left, ary);
  ary.push(root.val);
    preorderTraversal(root.right, ary);
  }
  return ary;
};

// 后续遍历
var postorderTraversal = function(root) {
 if (root !== null) {
    preorderTraversal(root.left, ary);
    preorderTraversal(root.right, ary);
  ary.push(root.val);
  }
  return ary;
};

由此也可以看出三种遍历以及名称的联系。

扩展

也就是说，限制使用递归来遍历树，这里以前序遍历为例（中序和后序思路相同，只是处理节点的位置不同）。

用过调试器的小伙伴都知道有个东西叫函数调用栈，用于记录函数的调用逻辑，当调用函数的时候将函数入栈，返回的时候出栈。而所谓递归就是函数自己调用自己，本质上也是函数调用，所以这里我们可以用借助栈来模拟递归。

在此基础上，如果我们想要完整的遍历一棵树，大致的思路应该如下：

• 首先令 current 指向当前节点，并将其入栈
• 随后令 current 指向 current.left
• 当左子树遍历到头的时候，通过出栈取出上级节点，遍历它的右子树，即令 current 指向 current.right

代码如下：

var preorderTraversal = function (root) {
  let current = root;
  const treeStack = [];
  while (current || treeStack.length > 0) {
    while (current) {
      treeStack.push(current);
      current = current.left;
    }
    current = treeStack.pop();
    current = current.right;
  }
};

这个时候，再完成前序遍历就很简单了，只需要先处理自己，再处理左右即可：

var preorderTraversal = function (root) {
  let current = root;
+ const treeNode = [];
  const treeStack = [];
  while (current || treeStack.length > 0) {
    while (current) {
 +    treeNode.push(current.val);
      treeStack.push(current);
      current = current.left;
    }
    current = treeStack.pop();
    current = current.right;
  }
  return treeNode;
};

结果如下：