【PHP】你知道MySQL索引为什么要选择B+树呢

声明

本文所述的各种数据结构(二叉树等)，均不考虑重复值的情况，本文简述各种数据结构的区别仅仅只是为了理解MySQL索引的需要而做的铺垫。

什么是索引

提起索引，大家都知道，建立索引可以让数据库查询更快，那么索引究竟是什么？我想这就不是每个人都能说得出来了。

索引，是数据库管理系统中一个排序的数据结构，并用以协助快速查询、 更新数据库表中数据。

是的，索引是一种数据结构，但是那么多的数据结构中为何MySQL要选择B+树呢？接下来就让我们一起来了解下B+树相对于其他数据结构有何独特之处！

二分查找法(Binary Search)

首先让我们自己想一想，如果让我们去设计，我们会怎么去存储？我想大部分人想到就是用链表或者数组去存储数据，然后再按默认的顺序排好，再去查找，而一个排好顺序的链表我们就可以通过二分查找法来高效查询。

二分查找也称折半查找，是一种效率较高的查找方法。比如有1-10十个数，我们要找到8，先从中间开始找5，然后发现8比5大，可以把5左边的数去掉，剩下6-10，再从中间开始找，依次类推，直到找到8为止。但是这种查找法有一个前提是数据必须是有序的，而且这种属于链表式的存储，我们一但要插入或者修改一个数据，可能会伴随着大量的下标移动，比如我们把1-10放在数组里面，下标分别对应0-9，然后现在要插入一个0，为了保证有序，0必须排在第一位，那么1-10所有的数据下标都要往后移动一位，这种就有点大动干戈了，所以为了解决这个问题，我们就有了二叉树。

二叉查找树(BST）

二叉查找树简称二叉树(BST)，英文全称：Binary Search Tree，这是一种什么样的数据结构呢？请看下图

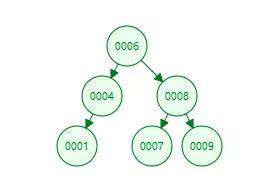
在上面这棵树中，我们要找到8，先从根节点6开始比较，发现8比6大，就往右边走，就可以找到8

二叉树的特点

二叉树有两个特点：

1、左子树所有的节点都小于父节点

2、右子树所有的节点都大于父节点

二叉树存在的问题

二叉树有一个严重的问题，那就是它的查找耗时是和这棵树的深度相关的，在最坏的情况下时间复杂度会退化成 O(n)。

如下图：

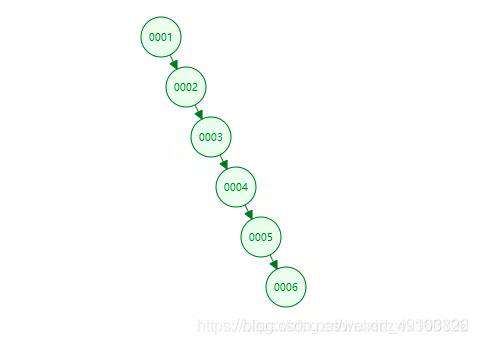
上面就是一种极端情况下的二叉树，会退化成线性链表，这种如果要找到最后一个数6，就要从1开始遍历完整棵树，效率就会非常低。那么有没有一种相对平衡一点，不要出现这种极端情况的数据结构呢，所以就有了平衡二叉树。

平衡二叉树(AVL Tree)

平衡二叉树，英文全名叫做 Balanced binary search trees，简称AVL树，这个AVL并不是英文名的简称，而是发明者(G. M. Adelson-Velsky和E. M. Landis)两个人的人名缩写，请看下图一个平衡二叉树示例：

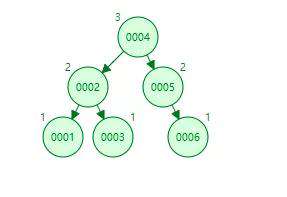
上图中也是从1开始插入6，如果是二叉树就会变成一种线性结构，但是平衡二叉树就会通过左旋和右旋操作，最终会生成上图所示的结构，感兴趣的可以进入网站自己操作观察旋转过程.

平衡二叉树的特点

平衡二叉树相比较二叉树具有一个特点就是：左右子树深度差绝对值不能超过 1，当然，平衡二叉树首先是一颗二叉树，只不过通过左旋和右旋实现左右子树深度差不超过1，避免了二叉树的极端情况的出现。

MySQL为何不选择平衡二叉树

既然平衡二叉树解决了普通二叉树的问题，那么mysql为何不选择平衡二叉树作为索引呢?

索引需要存储什么

让我们想一想，如果我们要把索引存起来，那么应该存哪些信息呢，它应该存储三块信息：

• 索引的值：就是表里面索引列对应的值。

• 数据的磁盘地址(通过磁盘地址找到当前数据)或者直接存储整条数据。

• 子节点的引用：我们需要从根节点往下走，所以需要知道左右子节点的地址。

根据这三点，可以有如下大致的一个简单的结构图：

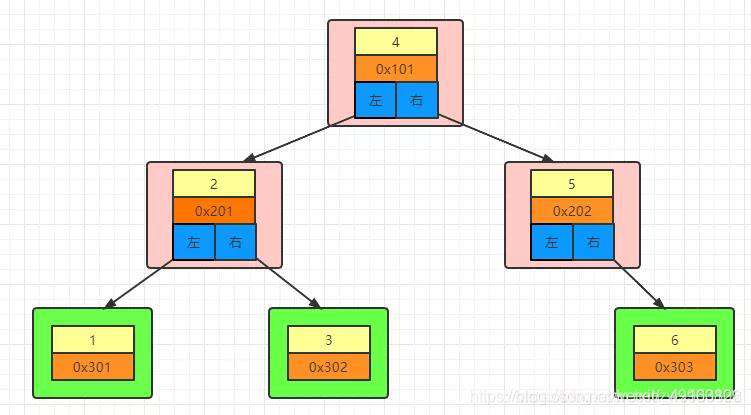
上图中数字表示的是索引的值，0x开头的表示磁盘地址，根节点中存了左右节点的引用。

AVL树用来存储索引存在什么问题

我们知道，页（Page）是 Innodb 存储引擎用于管理数据的最小磁盘单位，页的默认大小为16KB。页也就是上图中的节点，每查询一次节点就需要进行一次IO操作，IO操作是一种非常耗时的操作，很多业务系统的瓶颈都是卡在IO操作上，所以如果我们需要提高查询效率的办法之一就是减少IO次数，那么问题就来了，AVL树一个节点上只存了一个关键字(索引值)+一个磁盘地址+左右节点的引用，这是远远达不到16KB的，会浪费了大量的空间。

上图中如果我们要找到6这条数据，需要进行3次IO(获取一个节点就是一个IO操作)，如果这棵树很高的话，就会进行大量的IO操作，所以说AVL树存在的最大问题就是空间利用不足，浪费了大量空间，数据量大的时候就会成为一颗瘦高的树。

那么我们可以怎么改进呢？答案很明显了，那就是每个磁盘块多存一点东西，也就是说每个磁盘多存几个关键字，因为关键字越多，路数越多；路数越多，树也就越矮越胖，相应的操作IO次数就会越少。

多路平衡树(Balanced Tree)

多路平衡树简称B树，又称B-树，和AVL树一样，B树在枝节点和叶子节点存储键值、磁盘地址、左右节点引用。请看下图的一个多路平衡树的示例：

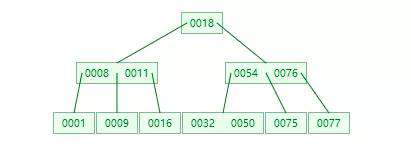
B树的特点

相比较AVL树，B树一个磁盘上可以存多个关键字(值)，而且有一个特点就是：

• 分叉数（路数）永远比关键字数多1。

我们可以画出如下简图(下图中只画了3路，即两个关键字，实际取决于一页能存储多少个关键字)：从上图可以很明显的看出，同样高度的树，B树能存的数据远远大于平衡二叉树。

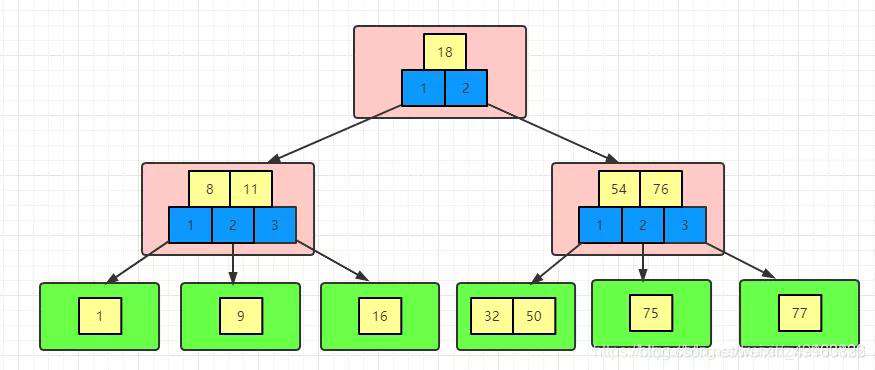
B树是如何查找数据的

以上图为例，假如我们要找key=32这个数字，首先获取到根节点，发现18小于key，所以往右边走，获取到右边的数据，54和76，这时候遵循以下原则：

• key<54,命中最左边分叉；

• key=54,直接命中，返回数据；

• 54<key<76,走中间的一个分叉；

• key=76,直接命中，返回数据；

• key>76，命中右边分支；

这里因为key=32，所以走得是第1条，命中左边分支，这时候再去获取左边分支，获取到32和50，比较发现key=32，命中，返回数据。

从上面我们可以看出B树效率相对于AVL树，在数据量大的情况效率已经提高了很多，那么为什么MySQL还是不选择B树作为索引呢？

那么接下来让我们先看看改良版的B+树，然后再下结论吧！

B+树

B+树由B树改良而来，属于改良版的多路平衡查找树。

首先让我们来看看B+树到底长什么样呢：

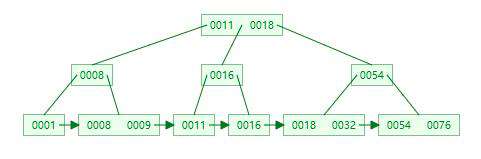
对比B+树，我们可以发现一个很明显的区别就是叶子节点有一个箭头指引而且从左到右是有序的。

InnoDB中使用的B+树相比较于传统B+树，改进之后的B+树具有以下特点

InnoDB中B+树的特点

• 它的关键字的数量是跟路数相等的。

• B+树的根节点和枝节点中都不会存储数据，只有叶子节点才存储数据。而搜索到关键字不会直接返回，会到最后一层的叶子节点。

• B+树的每个叶子节点增加了一个指向相邻叶子节点的指针，它的最后一个数据会指向下一个叶子节点的第一个数据，形成了一个有序链表的结构。

• 它是根据左闭右开的区间来检索数据的

按照B+树的特点，我们可以画出一个存储数据的简图，如下：

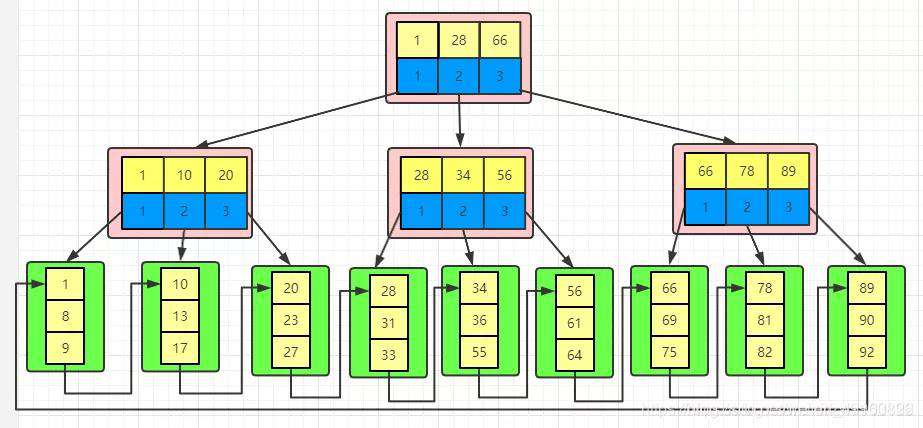
B+树是如何查找数据的

假设我们现在要找一个key=66，遵循如下步骤：

1、获取到根节点，依据左闭右开有如下区间：[1,28)，[28,66),[66,+∞)，命中了最后一个区间，虽然66在根节点，但是因为根节点不存储数据，所以是会往下继续搜索右边的节点

2、获取到右边节点，依据左闭右开有如下区间：[66,78),[78,89),[89,+∞)，命中左边的范围。

3、获取到第三排倒数第二块磁盘，找到66，返回数据。

B+树相对于B树的改进点

B+树是由B树改进而来的，所以B树能解决的问题，B+树都能解决，那么B+树能解决哪些B树所不能解决的问题呢？

1、扫库、扫表能力更强：如果我们要对表进行全表扫描，只需要遍历叶子节点就可以 了，不需要遍历整棵B+Tree

2、B+Tree 的磁盘读写能力相对于 B Tree 来说更强：根节点和枝节点不保存数据区， 所以一个节点可以保存更多的关键字，一次磁盘加载(IO操作)能获取到相对更多的关键字。

3、天然具备排序能力：叶子节点上有下一个数据区的指针，数据形成了链表。

4、效率稳定：B+Tree 永远是在叶子节点拿到数据，所以 IO 次数是稳定的，而B树运气好根节点就拿到数据，运气不好就要到叶子节点才能拿到数据，所花费的时间会有差异。

总结

本文简述了从二叉树到B+树之前的演进过程，并大致讲解了各种数据结构之间的差异以及MySQL为何最终会选择了B+树来作为索引。

点关注，不迷路

好了各位，以上就是这篇文章的全部内容了，能看到这里的人呀，都是人才。之前说过，php方面的技术点很多，也是因为太多了，实在是写不过来，写过来了大家也不会看的太多，所以我这里把它整理成了PDF和文档，如果有需要的可以

点击进入暗号: PHP+「平台」

更多学习内容可以访问【对标大厂】精品PHP架构师教程目录大全，只要你能看完保证薪资上升一个台阶（持续更新）

以上内容希望帮助到大家，很多PHPer在进阶的时候总会遇到一些问题和瓶颈，业务代码写多了没有方向感，不知道该从那里入手去提升，对此我整理了一些资料，包括但不限于：分布式架构、高可扩展、高性能、高并发、服务器性能调优、TP6，laravel，YII2，Redis，Swoole、Swoft、Kafka、Mysql优化、shell脚本、Docker、微服务、Nginx等多个知识点高级进阶干货需要的可以免费分享给大家，需要的可以加入我的 PHP技术交流群